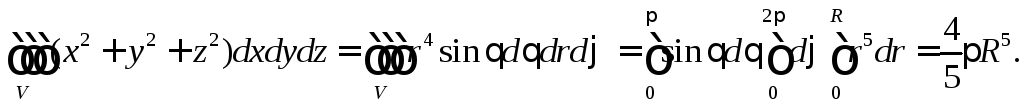7.5. Двойной интеграл в полярной системе координат

Для того чтобы двойной интеграл в декартовых координатах преобразовать в двойной интеграл в полярных координатах, нужно в подинтегральной функции заменить,, а элемент площадизаменить его выражением в полярных координатах.

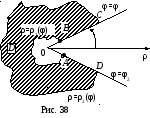●Правило расстановки пределов интегрирования (рис. 38)

1. Внутренний интеграл всегда за-висит от переменной ρ, считая φ постоянной величиной.

2. Чтобы расставить пределы внут-реннего интеграла, надо провести лучи,

исходящие из полюса. Точки входа и точки выхода лучей в область D, заданную системой неравенств: 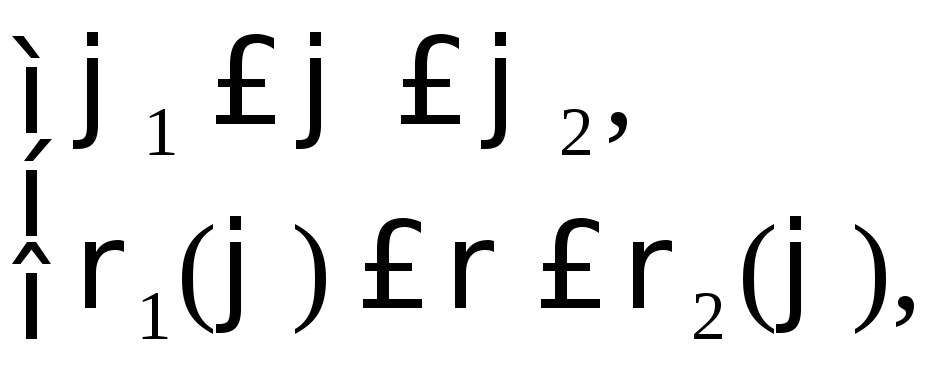определяют соответствен-но нижний и верхнийпределы интегрирования.

3. Пределы внешнего интеграла определяются уравнениями лучей и, считая против хода часовой стрелки (в положительном направлении).

4. Если полюс содержится внутри области D, то нижний предел внутреннего интеграла следует положить . Итак,

.

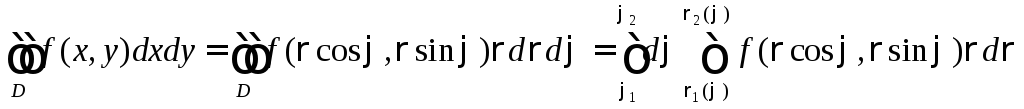Замечания.

1. Пределы интегрирования будут постоянными, если область интегрирования представляет собой часть круга.

2. К полярным координатам удобно переходить в том случае, когда область интегрирования ограничена дугами окружностей или линиями, заданными в полярных координатах.

Пример. Вычислить где

Решение. Перейдем к полярным координатам:

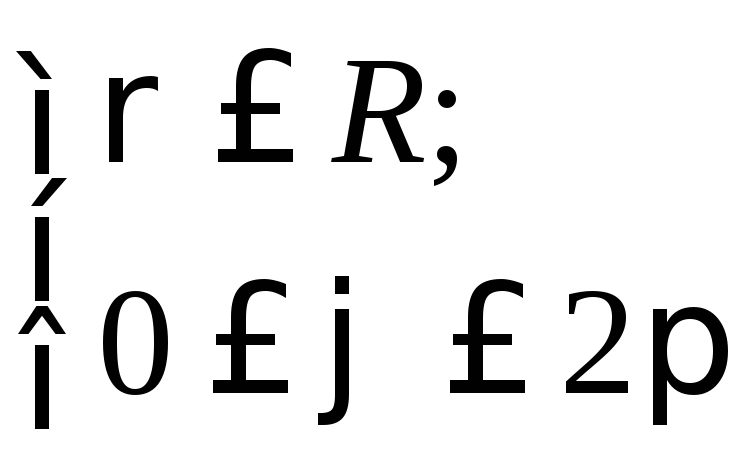По условию задачи следовательно,. Итак,

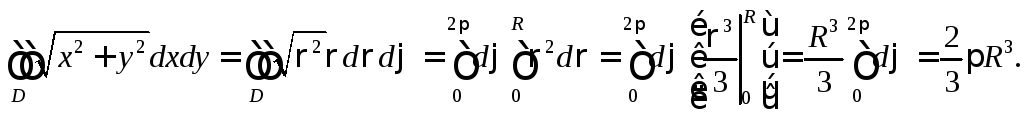
7.6. Тройной интеграл

По аналогии с двойным интегралом вводится понятие тройного интеграла по ограниченной замкнутой пространственной области V, если в ней определена непрерывная функция , который обозначается так:. Предположим, что областьV является стандартной в направлении оси , т. е. удовлетворяющей следующим условиям:

1) всякая прямая, параллельная оси и имеющая с областьюV общие точки, пересекает границу области только в двух точках;

2

Рис. 39

) проекцияD области V на плоскость представляет стандартную область в направлении осиили оси.

Если при этом область V ограничена сверху поверхностью , а снизу – поверхностью, то тройной интеграл в декартовых координатах можно вычислить следующим образом:

.

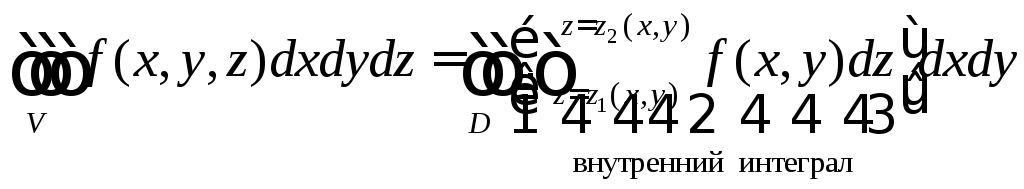Если, например, область D является стандартной в направлении оси и определяется неравенствами;, то

.

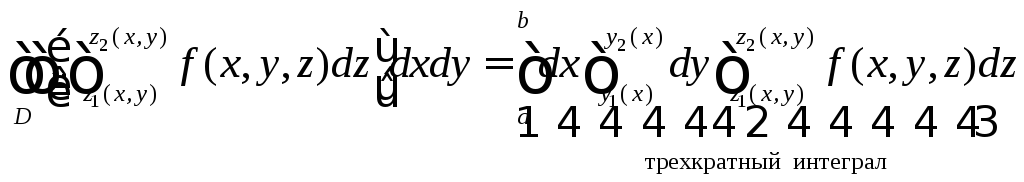Итак, .

Часто удобно вычисление тройного интеграла провести в цилиндрических или сферических координатах.

Цилиндрические координаты:

,

,

, где

При этом: .

Итак, тройной интеграл в цилиндрических координатах записывается следующим образом:

.

Пример 6.2. Вычислить

Рис. 40

где область V ограничена плоскостями цилиндроми расположена в первом октанте (рис. 40), т. е.

Решение. Вычислим в цилиндрической системе координат

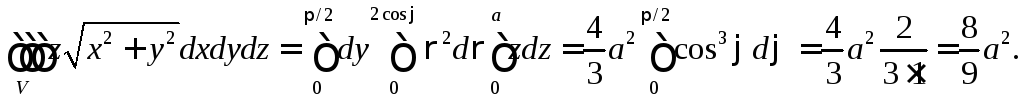
Сферические координаты:

,

,

,

где

При этом: .

Тройной интеграл в сферических координатах записывается так:

Особенно удобно применение сферических координат в случае, когда область интегрирования V-шap с центром в начале координат или шаровое кольцо.

Пример 6.3. Вычислить

где V – шар, который описывается неравенством (рис. 41).

Р

Рис. 41

ешение. Перейдем к сферическим координатам. При этом подынтегральная функция примет вид . Следовательно