7.3.2. Интегралы от разрывных функций
Пусть
область задания функции
– промежуток
или
,
но в точке
b
предел
,
при этом
называетсяособой
точкой. И в
том и в другом случаях, по определению,
.
Если этот предел существует, то интеграл
называетсясходящимся
несобственным
интегралом.
В случае, если
,
то обозначают:
и этот интеграл называютрасходящимся.
Аналогично
определяется несобственный интеграл
от функции, заданной на промежутках
или
,
но при этом
.
Наконец,
если функция задана на всем отрезке
за исключением его внутренней точки
,
т. е. функция определена на промежутках
и
или
,
то несобственный интеграл определяется
так:
Пример.
– особая точка подинтегральной функции
=
–сходится.
Формула Ньютона-Лейбница
,
где
● При
исследовании несобственных интегралов
от разрывной функции на сходимость
можно применять формулу Ньютона-Лейбница
только тогда, когда первообразная
функция от
в особой точке непрерывна.
Примеры.
1)
– особая точка функции
.
Первообразная
– непрерывна в особой точке
можно применять формулу Ньютона-Лейбница
данный несобственный интеграл сходится.
2)
– всюду непрерывна
–сходится.
7.4. Двойной интеграл
Двойной
интеграл от непрерывной функции
обладает всеми свойствами определенного
интеграла. Вычисление двойного интеграла
сводится к вычислению двух определенных
интегралов.
|
1)
Область интегрирования
Рис. 33
При
вычислении внутреннего интеграла
величину х
считают постоянной, а любая прямая
|
2)
Область интегрирования
у
d В D
Р Q
х=φ1(у) линия
входа
х=φ2(у) линия
выхода
С D
А С
0 х Рис. 34
При
вычислении внутреннего интеграла
величину у
считают постоянной, а любая прямая
|
|
Если
нижняя или верхняя границы области
состоит из нескольких участков с
различными уравнениями, то область
D
следует разбить прямыми, параллельными
оси
Рис. 35 |
Если
левая или правая граница будет
состоять из нескольких участков с
различными уравнениями, то область
D
следует разбить прямыми, параллельными
оси
Рис. 36 |
|
причем
|
причем
|
(рис. 33)
ограничена слева и справа прямыми
и
,
а снизу и сверху непрерывными кривыми
и
,
причем
.
,
параллельная оси
,
пересекает областьD
не более чем в двух точках: на «линии
входа»
и на «линии выхода»
.
Пределы внешнего интеграла определяются
проецированием областиD
на ось
:
в областиD
переменная х
изменяется на отрезке
.
(рис. 34)
ограничена снизу и сверху прямыми
и
,
а слева и справа
непрерывными
кривыми
и
,
причем
,
параллельная оси
,
пересекает областьD
не более чем в двух точках: на «линии
входа»
и на «линии выхода»
.
Пределы внешнего интеграла определяются
проецированием областиD
на ось
:
в областиD
переменная у
изменяется на отрезке
.
,
на части:
(рис. 35).
,
на части:
(рис. 36).
,
;
,
;
П
ример
1.3. Изменить
порядок интегрирования
Решение.
По данным пределам интегрирования
опишем область D
(рис. 37) системой неравенств
.
Построим область интегрированияD
и изменим порядок интегрирования:
.
Следовательно,
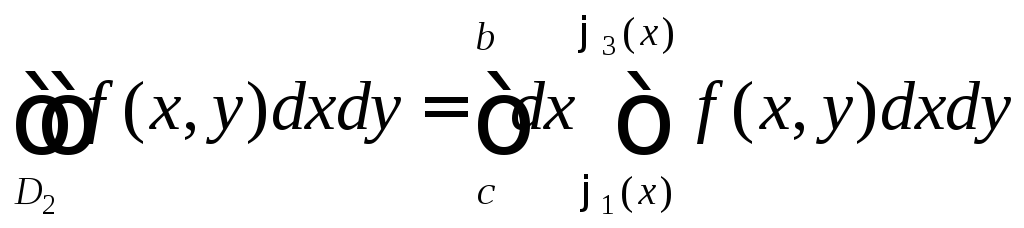
