6.3. Геометрический и механический смысл производной функции одной переменной

● Геометрический смысл производной функции одной переменной. Числовое значение производной функции в точке есть угловой коэффициент касательной, построенной к графику данной функциив данной точке с абсциссой. Следовательно,где α – угол наклона касательной к положительному направлению оси абсцисс.

●Уравнение касательной к гра-фику функции в точке:

Уравнение нормали:

или

● Механический смысл производной.

Если – функция зависимости пути материальной точки от времени, то–скорость движения этой точки, а –ускорение движущейся точки в любой момент времени . Значит

Пример 1. Записать уравнение касательной к графику функции , которая параллельна прямой .

Решение. Угловой коэффициент касательной т. к. по условию касательная параллельна прямойС другой стороны,гдеСледовательно,Далее составим уравнение касательнойсчитаяПри этомПодставляя найденные числовые значения,в уравнение касательной, получим:

или

Пример 2. Найти скорость движения точки, движущейся вдоль оси по законув тот момент времени, когда ускорение движения равно нулю.

Решение. Ускорение скорость движения

Определяем По условию задачиследовательно,Далее находим скорость в момент времени

Итак, скорость равна в тот момент времени, когда ускорение движения равно нулю.

6.4. Частные производные функции двух переменных

Если дважды дифференцируемая функция по каждой переменной, то

;

; ;;

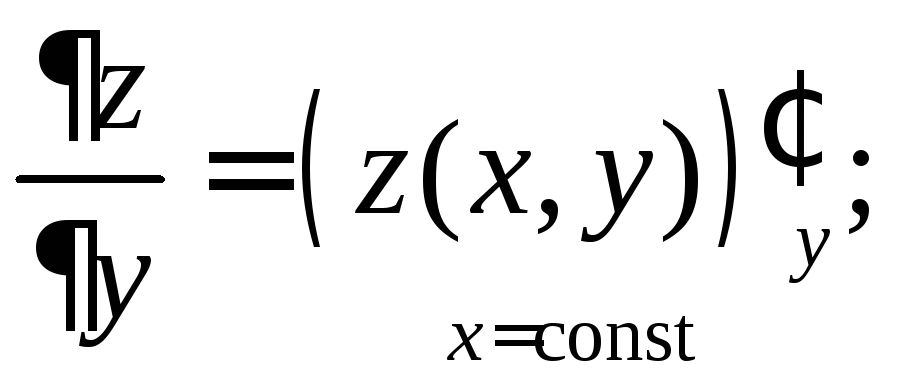
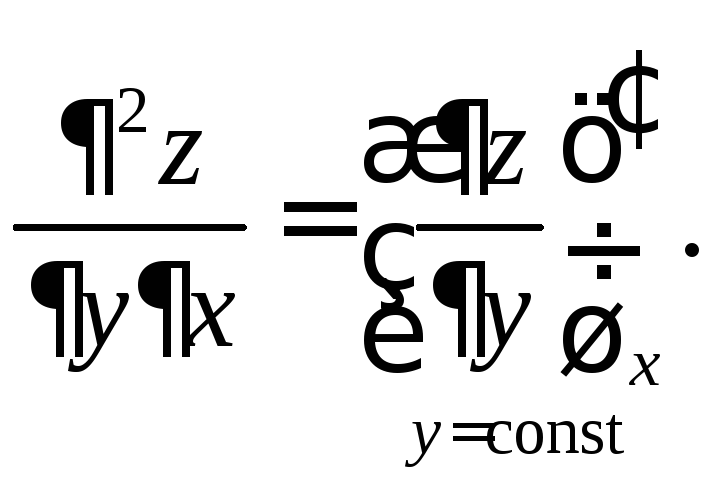
При этом смешанные производные второго порядка равны между собой:

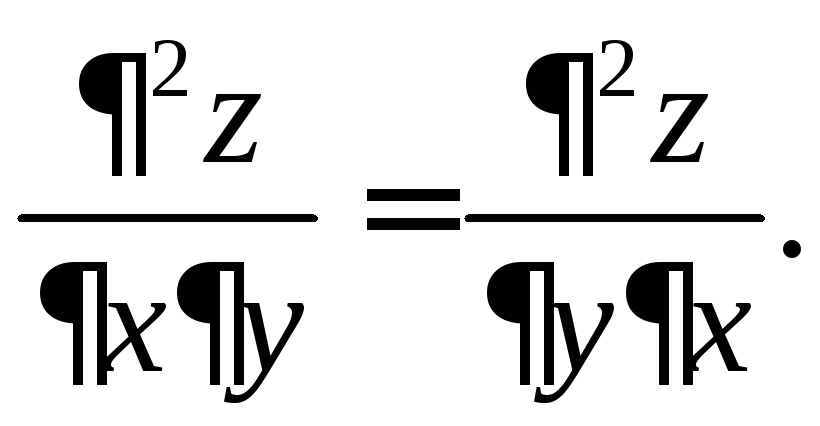
6.5. Исследование функций

6.5.1. Теоремы ролля, лагранжа, коши и формула тейлора

Теорема Ролля. Если функция непрерывна на отрезкеи дифференцируема в интервалеи еслито в интерваленайдется хотя бы одно значение, при котором(касательная к кривойв точкепараллельна оси).

Если в частности ,, то теорема Роля означает, что между двумя корнями функции содержится хотя бы один корень ее производной.

Теорема Лагранжа (о конечном при-ращении). Если функция непрерывна на отрезкеи дифференцируема в интервале, то в этом интервале найдется хотя бы одно значение, при котором выполняется равенство

(касательная в точке параллельна хордеАВ).

Теорема Коши. Если функции инепрерывны на отрезкеи дифференцируемы в интервале, причем, то в этом интервале найдется хотя бы одно значение, при котором

где

Формула Тейлора. Функция , дифференцируемаяраз в некотором интервале, содержащем точкуа, может быть представлена в виде суммы многочлена n-й степени и остаточного члена следующим образом:

где , причем.

При получаетсяформула Маклорена

.

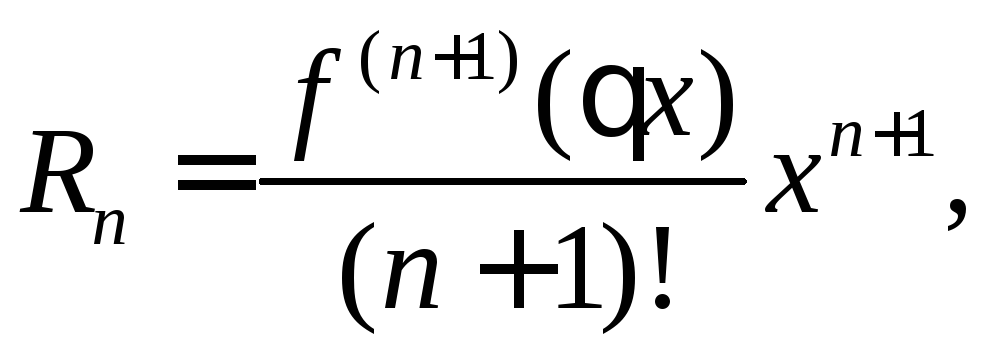
6.5.2. Правило лопталя раскрытия неопределенностей

Пусть функции идифференцируемы в-окрестности точки и. Еслиилит. е. частное представляет собой в точкенеопределенность видаили, топри условии, что существует предел отношения производных.

Если частное в точкетакже есть неопределенность видаилии производныеиудовлетворяют соответствующим условиям, то следует перейти к отношению вторых производных и т. д.