matan

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Московский государственный университет экономики статистики и информатики Московский международный институт эконометрики, информатики, финансов и права

Геворкян Э.А. Малахов А.Н. Фохт А.С.

Щербакова Н.С.

МАТЕМАТИЧЕСКИЙ АНАЛИЗ

(ЧАСТЬ I)

Москва, 2001

Содержание:

Введение…………………………………………………………………………………..5

Раздел I. Теория последовательностей и функций одной переменной……………….6

1.1.Множество вещественных чисел………………………………………………...6

1.2.Ограниченные и неограниченные множества вещественных чисел…………..7

1.3.Некоторые конкретные числовые множества…………………………………..9

1.4.Понятие числовой последовательности……………………………………..…10

1.5.Бесконечно большие и бесконечно малые числовые последовательности….11

1.6.Сходящиеся числовые последовательности. Предел числовой последовательности..…………………………………………………………………16

1.7.Основные свойства сходящихся числовых последовательностей…..………..17

1.8.Монотонные числовые последовательности…………………………..……….18

1.9.Число е……………………………………………………………………..……...20

1.10.Предельный переход в неравенствах……………………………………..…...21

1.11.Подпоследовательности числовых последовательностей………………..….22

1.12.Функция одной переменной…………………………………………………...23

1.13.Предел функции………………………………………………………………...24

1.14.Бесконечно большие и бесконечно малые функции…………………………27

1.15.Свойства функций, имеющих предел…………………………………………29

1.16.Замечательные пределы………………………………………………………..29

1.17.Сравнение бесконечно малых функций……………………………………….32

1.18.Непрерывность функций в точке………………………………………………33

1.19.Классификация точек разрыва…………………………………………………34

1.20.Определение непрерывности функции в точке с использованием понятия приращения функции…………………………………………………………………35

1.21.Арифметические действия над непрерывными функциями…………………36

1.22.Непрерывность сложной функции…………………………………………….36

1.23.Свойства функций, непрерывных на сегменте……………………………….36

Примеры……………….………………………………………………………………….39

Тест………………………………………………………………………………………..46

Раздел II. Дифференциальное исчисление функции одной переменной…………….48

2.1.Определение производной функции первого порядка………………………...48

2.2.Геометрический смысл производной…………………………………………...49

2.3.Дифференцируемость функции. Дифференциал функции и его геометрический смысл………………………………………………………………..50

2.4.Правила вычисления производных, связанных с арифметическими действиями над функциями…………………………………………………………..53

2.5.Производные элементарных функций. Производная обратной функции……54

2.6.Правила диференцирования сложной функции. Инвариантность

формы первого дифференциала……………………………………………………...57 2.7. Дифференцирование степенно-показательной функции и функций, заданных параметрически и в неявном виде………………………………………..58

2.8.Производные и дифференциалы высших порядков……………………………59

2.9.Возрастание (убывание) функции в точке. Локальный экстремум. Теорема о нуле производной (теорема Ролля)…………………………………………………..62

2.10.Формула конечных приращений (теорема Лагранжа). Обобщенная

формула конечных приращений (теорема Коши)…………………………………..65

2.11.Раскрытие неопределенностей (правила Лопиталя)………………………….67

2.12.Формула Тейлора с остаточным членом в форме Шлемильха-Роша,

Лагранжа, Коши и Пеано……………………………………………………………..70

3

2.13.Формула Маклорена. Разложение по формуле Маклорена некоторых элементарных функций……………………………………………………………….71

2.14.Интервалы монотонности и точки экстремума функции…………………….74

2.15.Направление выпуклости графика функции. Точки перегиба……………….76

2.16.Асимптоты графика функции. Схема исследования функции и построение ее графика……………………………………………………………………………...78

Примеры……………….…………………………………………………………… ……80 Тест………………………………………………………………………………………..87

Раздел III. Дифференциальное исчисление функции нескольких переменных……...89

3.1.Определение m-мерного евклидова пространства и области…………………89

3.2.Предел функции нескольких переменных……………………………………...90

3.3.Непрерывность функций нескольких переменных ……………………………92

3.4.Частные производные функций нескольких переменных первого и высших порядков...……………………………………………………………………………..93

3.5.Дифференцируемость и дифференциал функции нескольких переменных….97

3.6.Производная функции нескольких переменных по направлению. Градиент. Касательная плоскость и нормаль к поверхности…………………………………..99

3.7.Дифференциалы высших порядков функции нескольких переменных……..102

3.8.Формула Тейлора для функции нескольких переменных……………………104

3.9.Локальный экстремум функции нескольких переменных…………………...105

3.10.Условный экстремум функции нескольких переменных…………………...107

Примеры………………..………………………………………………………………..110 Тест………………………………………………………………………………………114

Раздел IV. Неопределенный интеграл…………………………………………………117

4.1.Определение неопределенного интеграла…………………………………….117

4.2.Основные правила интегрирования……………………………………………118

4.3.Интегрирование заменой переменной…………………………………………120

4.4.Интегрирование по частям. Применение этого метода при вычислении некоторых важных интегралов……………………………………………………...121 4.5.Интегрирование дробно-рациональных функций. Метод Лагранжа………...126 4.6.Интегрирование тригонометрических выражений……………………………131

4.7.Интегрирование дробно-линейных иррациональностей и дифференциальных биномов………………………………………………………..134 4.8.Интегрирование квадратичных иррациональностей. Подстановки Эйлера…135

Примеры……………….………………………………………………………………...139 Тест.………………………………………………………………………………………144

Раздел V. Определенный интеграл и его применение…………………………..……147

5.1.Определение определенного интеграла……………………………………….147

5.2.Верхняя и нижняя интегральные суммы Дарбу и их свойства………………148

5.3.Интегрируемость функций. Свойства определенного интеграла. Формула среднего значения определенного интеграла……………………………………...150

5.4.Вычисление определенного интеграла по формуле Ньютона-Лейбница…..155

5.5.Вычисление длин дуг плоских кривых………………………………………..157

5.6.Вычисление площадей плоских фигур………………………………………...159

5.7.Вычисление площадей поверхностей и объемов тел вращения……………..162

Примеры………………..………………………………………………………………..165 Тест………………………………………………………………………………………169

Итоговый тест…………………………………………………………………………...171

Литература………………………………………………………………………………179

4

бесконечные непериодические десятичные дроби. Для единообразного представления всех чисел в форме бесконечной десятичной дроби в случае целых чисел или конечных десятичных дробей принята двоякая

Бесконечные десятичные дроби образуют множество R вещественных чисел. Описанный подход к введению понятия вещественного числа является одним из возможных и ориентирован на традиционно сложившуюся веками десятичную систему счета. В настоящее время используются и другие системы счета, например двоичная. Однако, при любом подходе результат расчета или измерения представляется с помощью рациональных чисел, отражающей этот результат с нужной точностью.

Ниже приведем основную символику алгебры логики, которые мы

вдальнейшем будем использовать при изложении материала.

1.- символ, означающий “каково бы ни было”, “для любого”.

2.- символ, означающий “существует”.

3.: - символ, означающий “такое, что”, “выполняется”, “удовлетворяет условию”.

4.- символ, означающий “принадлежит”.

5.def - символ, означающий “определяется”.

6.U(x0) - означает “некоторая окрестность точки х0”.

7.Uδ(x0) - означает “δ-окрестность точки х0”.

8. U (x0 ) - означает “проколотая окрестность точки х0” (окрестность точки х0, за исключением быть может самой точки х0).

1.2.Ограниченные и неограниченные множества

ьвещественных чисел

Определение 1.1. Множество вещественных чисел {x} называется ограниченным сверху (снизу), если существует такое вещественное число М(m), что каждый элемент множества удовлетворяет неравенству x ≤ M (x ≥ m ). При этом число М(m) называется верхней (нижней) гранью множества.

В символической форме это записывается так:

def

({x} ограничено сверху) ≡ ( M R)( X {x}: X ≤ M),

def

({x} ограничено снизу) ≡ ( m R)( X {x}: X ≥ m). (1.1.1.)

7

Рассмотрим, например, множество {x} всех правильных рациональных дробей qp , p Z, q Z, q≠0. |p|<|q| (рис. 1.2.).

Рис. 1.2.

Так как модуль любого из этих чисел меньше 1, то все они удовлетворяют неравенствам -1< qp <1. Поэтому любое число ≥ 1 может

служить для этого множество верней гранью, а любое число ≤ -1 - нижней гранью. Геометрически это означает, что все точки числовой оси, соответствующие числам, образующим рассматриваемое множество, лежат слева от точки 1 и справа от точки -1, а любое число, лежащее вне указанной области, может рассматриваться как верхняя (≥ 1) или как нижняя (≤ -1) грань.

Естественно, возникает вопрос о существовании наименьшей из всех верхних граней ограниченного сверху множества и наибольшей из всех нижних граней ограниченного снизу множества.

Определение 1.2. Наименьшая из всех верхних граней ограниченного сверху множества {x} называется точной верхней гранью этого множества и обозначается символом x = sup{x} (supremum - наивысшее).

Наибольшая из всех нижних граней ограниченного снизу множества {x} называется точной нижней гранью этого множества и обозначается символом x = inf {x} (infimum - наинизшее).

Определение 1.2. можно сформулировать и по-другому, более конструктивно.

Определение 1.3. Число x ( x ) называется точной верхней (нижней) гранью множества {x}, если выполняются два требования:

1.для всех элементов множества {x} справедливо x ≤ x (x ≥ x );

2.для любого положительного (сколь угодно малого) вещественного числа ε найдется хотя бы один элемент x* множества {x}, удовлетворяющий неравенствам x -ε < x* ≤ x ( x ≤ x* < x +ε) (рис. 1.3.).

8

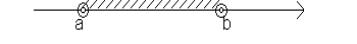
2. Интервал (“незамкнутый отрезок”) - вещественные числа, удовлетворяющие неравенствам a<x<b. Интервал обозначается символом (a;b) и не включает граничные точки (рис. 1.5.).

Рис. 1.5.

3.полусегмент или полуинтервал - множество вещественных чисел, которое включает одну из граничных точек. Полусегмент или полуинтервал обозначается символом [a;b) или (a;b].

4.окрестность точки а - интервал (a-ε1; a+ε2), где ε1 и ε2 положительные вещественные числа.

5.δ окрестность точки а - интервал (а- δ; a+ δ), где δ - положительное вещественное число.

6.числовая прямая - интервал (-∞; +∞).

Определение 1.5. Множество {x} называется неограниченным, если каково бы ни было положительное вещественное число А, найдется элемент х* этого множества, такой, что

|x*|>A.

В символической форме это определение запишется так:

def

({x} неограниченное) ≡ ( A>0, A R)( x* {x}) : (|x*|>A). (1.4.)

Примером неограниченного множества вещественных чисел может служить множество R (все точки на числовой оси).

1.4. Понятие числовой последовательности

Определение 1.6. Пусть каждому натуральному числу n N поставлено в соответствие по определенному правилу или закону вещественное число xn. Тогда множество занумерованных вещественных чисел

x1, x2, x3, ..., xn, ...

называется числовой последовательностью.

10