
matan
.pdf
|
|
|
|
9x |
2 |
+9x∆x +(∆x) |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
+∆x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
ln 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
3x3 +2 |
|
|
|
9x |
2 + |
∆ + ∆ |
2 |
|
9x |
2 |
|
|||||||||
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
9x x |
( |
x) |
|
= |
|
. |
|||
|
|
|
|
|
|
∆x |
|
|
|
|
|
|
|
3x3 +2 |
|
|
|
3x3 +2 |
||||||
∆x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
∆x→0 |
|
|
|
|
|
|
|
||||
|
|
' |
|
|
' |
|
|
3 |
|
9x2 |
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: |
f |
|
(x) = ln |
(3x |
|
+2) = |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
3x |
3 +2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 2. Найти производную функции y=f(x), если она задана:
а) в явном виде (y=f(x)= ln tg3 |
|
x |
|
+1 ); |
|
|||
6 |
|
|
||||||
|
|
|
|
|||||
|
|
|
3 |
|
|
|||
б) в параметрической форме |
y = |
|
|
; |
||||
e2t +1 |
||||||||
|
|
x = 4 −e−2t |
|
|||||
|
|
|
|
|
|
|
|
|
в) в неявном виде (3x+y-xyln3=15). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Решение: |
|
|
|
|
а) |
|
|
|
|
пользуясь |
|
|
|
|
правилами |
|
дифференцирования |
||||||||||||||||||||||||||||||||||||||||||||
элементарных и сложных функций, имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
|
sin |
2 |
x |
|
|
||||||||||
|
' |
|
' |
|
' |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
. |
||||||||||||||
y |
|
= f |
|
(x) = ln |
(tg |
|
|
|
|
+1) = |
|
|
|
|
|
|
|
3tg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
6 |
|
tg |
3 x |
|
|
6 |
|
|
|
|
|
2 x |
|
6 |
2 |
|
|
4 x |
|
|
|
3 x |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+1 |
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
tg |
|
|
|
+1 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
6 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
' |
|
|
3 x |
|
|
|
|
|
|
|
|
|
|
|
|
sin 2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
ln |
tg |
|
|
+1 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
6 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 cos |
|
|
|
|
|
tg |
|
|
|
|
|
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решение: б) Согласно (2.41) имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
y' = |
dy |
|
= |
y' (t) |
= |
|
|
|
|
|
|
|
|
|
−6e2t |
|
|
|
|
|
|
|
|
|
= − |
|
3e4t |
|
. |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
(e |
2t +1) |
2 (−2) (−e−2t ) |
(e2t +1)2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
dx |
|
|
|
x' (t) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
Ответ: |
y |
' |
= − |
|
|
|
3e4t |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
(e |
2t |
+1) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
81

Решение: в) Продифференцировав обе части уравнения, имеем
3x+y (1+ y' ) − y ln 3 − x ln 3y' = 0
Отсюда, решая последнее относительно y' , получим
y' = 3x+y − x .
Ответ: |
y' = |
y −3x+y |
. |
|
|||
|
|
3x+y −x |
|
Пример 3. Исследовать функцию f(x) и построить ее график, если:
а) f(x)= x2 +4 , б) f(x)= 3 x2 (x −5).
4x
Решение: а) f (x) = x2 + 4 4x
1. Данная функция определена для -∞<x<0 U 0<x<∞. Так как
f (x) = |
x2 + 4 |
≠ 0 ни при каком значении x и функция не определена при |
|
4x |
|||
|
|
x=0, то график этой функции не пересекается с координатными осями
Ox и Oy. Функция нечетная, так как |
f (−x) = |
(−x)2 |
+4 |
=− |
x2 |
+4 |
=−f (x). |
|||
−4x |
|
4x |
|
|||||||
|
|
|
|
|||||||
Значит, график функции симметричен относительно начала координат. Функция не является периодической. Точка x=0 есть точка разрыва второго рода.
2. Функция стремится к ± ∞ при x → ± ∞ , так как
lim f (x) = lim |
x2 |
+4x |
= |
1 |
lim x(1 |
+ |
4 |
) = ±∞ |
|
|
4x |
|
x |
||||||
x→±∞ |
x→±∞ |
|
|
4 x→±∞ |
|
|
|||
3. График функции имеет вертикальную асимптоту x=0 (ось Оy), потому что
lim f (x) = lim x2 +4 = ±∞
x→0±0 x→0±0 4x
Для нахождения наклонной асимптоты, вычисляем предел
82
lim f (x) = lim |
x2 |
+4 |
|
= |
1 |
lim (1 |
+ |
4 |
) = |
|
1 |
= k, |
|
|
|
|||||||||
4x x |
|
x2 |
4 |
|
|
|
||||||||||||||||||
x→±∞ |
x→±∞ |
|
4 x→±∞ |
|
|
|
|
|
|
|
|
|||||||||||||
lim ( f (x) −kx) = lim ( |
x2 +4 |
− |
x |
) = lim |
|
x2 |
+4 − x |
2 |
= lim |
1 |
= 0 |
=b |
||||||||||||
4x |
4 |
|
|
|
|
4x |
|
|
|
|
||||||||||||||
x→±∞ |
x→±∞ |
|
|
|
x→±∞ |
|
|
|
|
|
|
|
x→±∞ x |
|
|
|||||||||
Значит, прямая |
y = |
x |
является наклонной асимптотой для графика |
|||||||||||||||||||||
|
||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
данной функции.
4. Вычисляя производную первого порядка данной функции и приравнивая к нулю, получим
f ' (x) =( |
x2 +4 |
)' = |
1 |
|
|
x2 −4 |
|
=0 x2 |
−4 =0 x1 = −2, x2 = 2. |
|
4 |
x2 |
|||||||
|
4x |
|
|
|
|||||
То есть, необходимое условие экстремума дифференцируемой функции выполняется в точках x1 =-2, x2 = 2. И так как
f’(x < -2) >0 |
и |
f’(x |
> -2) < 0, |
f’(x < 2) < 0 |
и |
f’(x |
> 2) > 0, |
то согласно достаточному условию экстремума в точке x1 =-2 функция имеет максимум (fmax = f (-2) = -1), а в точке x2 = 2 функция имеет
минимум (fmin = f (2) = 1). |
> 2 f’(x) >0 и функция |
|
Нетрудно заметить, что при x < -2 и x |
||
монотонно возрастает, а при –2 < x < 0 и |
0 < x < 2 |
f’(x) < 0 и |
функция монотонно убывает.
5. Для определения интервалов сохранения направления выпуклости и точек перегиба графика функции, вычислим вторую производную f’’(x) данной функции. Имеем:
|
" |
|
x |
2 |
− |
4 |
|
' |
2 |
|
||
|
|
|
|
|
|
|||||||
f |
|
( x ) = |
|
|
|
|
|
|
= |
|
|
. |
|
|
4 x |
2 |
|
x |
3 |
||||||
|
|
|
|
|
|
|
|
|
|
|||
83
Так как f " (x) = x23 ≠ 0 ни при одном значении x, то график данной
функции не имеет точек перегиба. Для значений x < 0 f " ( x) = x23 0 и
график имеет направление выпуклости вверх, а для значений x > 0 f " ( x) = x23 0 и график имеет направление выпуклости вниз.
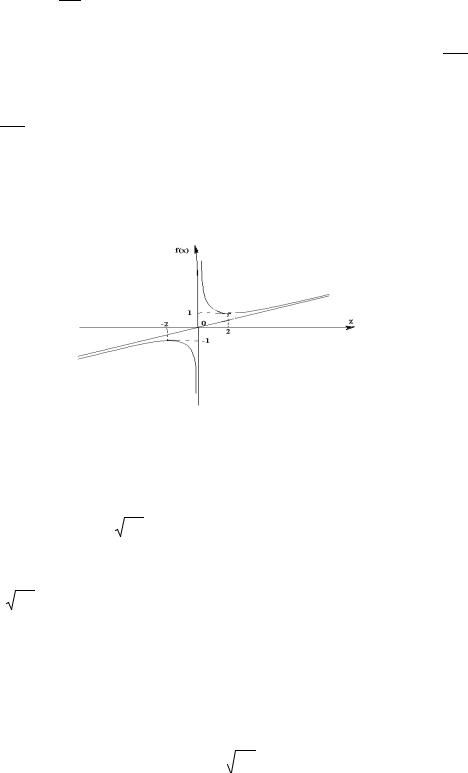
В заключении, пользуясь полученными результатами можно построить график функции (рис. 2.9.)
Рис. 2.9.
Решение: б) f (x) = 3 x2 (x −5)
1. Данная функция определена и непрерывна для всех -∞<x<∞. Так как f (x) = 3 x2 (x −5) = 0 при x1=0 и x2=5, а f (0) = 0 , то график данной функции пересекает ось Оx при x1=0 и x2=5, а ось Оy при x=0. Функция не обладает четностью. Она не является периодической.
2. Так как
lim f (x) = lim 3 x2 (x −5) = ±∞,
x→±∞ x→±∞
то нет горизонтальных асимптот y графика данной функции.
84
3. В силу непрерывности функции для x R ее график не имеет вертикальных асимптот. Для нахождения наклонных асимптот вычислим предел
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
f (x) |
3 |
x2 (x −5) |
= lim |
3 |
x |
2 |
|
− |
5 |
= ∞. |
||
x |
= lim |
|
x |
|
|
1 |
x |
|
|||||
x→±∞ |
x→±∞ |
|
x→±∞ |
|
|
|
|
|
|
|
|||
Последнее указывает на то, что график функции не имеет наклонных асимптот.
4. Вычислим производную первого порядка данной функции
f ' (x) =[3 x2 (x −5)]' = 2(3x3 −x5) +3 x2 = 53x3−x10 .
Из полученного выражения следует, что f’(2)=0 и f’(0) не существует. То есть точки x1 =2, x2 = 0 являются точками возможного экстремума
функции. Пользуясь достаточными |
условиями экстремума, |
||
устанавливаем, что при x1 = функция имеет минимум (fmin = f (2) = |
|||
−33 |
|
), а при x2 = 0 функция имеет максимум (fmax = f (0) = 0) . |
|
4 |
|||
|
|
Функция монотонно возрастает при x < 0 и x > 2, и монотонно |
|
убывает при 0 < x < 2. |
|
||
|
5. Вторая производная данной функции имеет вид |
||
f |
" |
5 x −10 |
|
' |
10 |
|
x +1 |
. |
||
|
( x) = |
33 x |
|
= |
9 |
3 |
x 4 |
|||
|
|
|
|
|
|
|
||||
Так как f |
" ( x) = |
10 |
x +1 |
= 0 при x |
= -1 и |
f " ( x−1) 0 , а |
|
|
9 |
3 x 4 |
|
|
|
f " ( x −1) 0 , |
то точка |
(-1;-6) |
является |
точкой |
перегиба графика |
|
данной функции.
Для x < -1 – направление выпуклости графика вверх, для x > -1 – направление выпуклости графика вниз.
На основании полученных выше результатов, теперь можно построить график данной функции (рис. 2.10.).
85
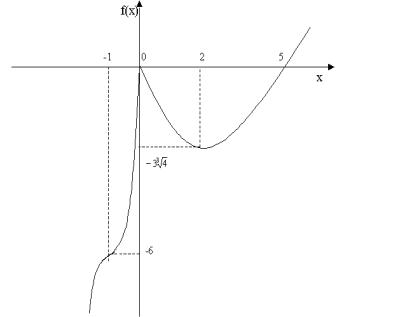
Рис. 2.10.
Тест
86

Используя правила Лопиталя, вычислить пределы:
1. lim e(2x −1 ). x→0 ln 1 +2x
а) 0; б) ∞; в) 2; г) 1.
1
2. lim x1−x .
x→1
а) 1;
б) е;
в) 1е ; г) ∞.
1
3. lim(2x + x)x .
x→0
а) 1;
б) е2;
в) 
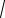 e3 ; г) 1e .
e3 ; г) 1e .
Найти точки экстремума функции:
4. y=xlnx. а) e(max);
б) 1e (min); в) e12 (max); г) 1(max).
5. y=1- 3 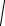 (x −4)2 .
(x −4)2 .
а) 0(min);
б) нет;
в) 4(max); г) 2(min).
87
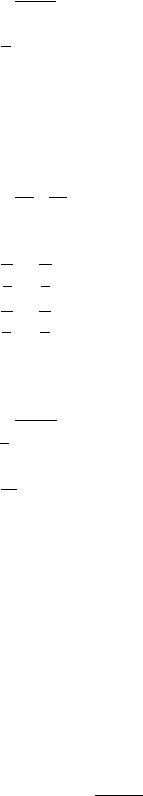
6.y = 3 − x2 .
x+2
а) -3(min);-1(max); б) 
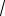 3 (min);0(max); в) -3(max;1(min);
3 (min);0(max); в) -3(max;1(min);
г) нет.
Найти абсциссы точек перегиба графика функции.
7. y = x14 − x22 .
а) 1;-1; б) 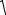
 53 ;-
53 ;- 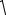
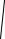 53 ;
53 ;
в) 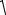
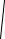 35 ;-
35 ;- 
 35 ; г) 2;-2.
35 ; г) 2;-2.
8. y = e lnx x .
а) 
 e ; б) 1;
e ; б) 1;
в) 
 e3 ; г) e.
e3 ; г) e.
Найти вертикальные, наклонные и горизонтальные асимптоты функции
9.y= 3 − 4x 2 .
x+ 2
а) х=-1; у=-4х-8; б) х=-2; у=-4х+8; в) х=-3; у=-2х+8; г) х=4; у=х+8.
10.y=2arctg x - x2 +3x .
x−4
а) x=3; y=-x+π;
б) x=4; y=-x+π-1; y=-x-π-1; в) x=-2; y=x+π;
г) x=1; y=x.
88

Раздел III. Дифференциальное исчисление функции нескольких переменных
3.1. Определение m-мерного евклидова пространства и области
Определение 3.1. Координатное пространство Am называется m- мерным евклидовым пространством Еm, если между любыми точками M′(x1′, x2′,... ,xm′) и M′′(x1′′, x2′′,... ,xm′′) координатного пространства Am определено расстояние ρ(М′,М′′) по формуле
ρ(M',M'')= 
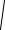 (x1'' − x1| )2 +(x''2 − x|2 )2 +...+(x''n − x|n )2 .
(x1'' − x1| )2 +(x''2 − x|2 )2 +...+(x''n − x|n )2 .
Определение 3.2. Множество {M} пространства Еm называется открытым множеством, если любая точка М(х1, х2,... хm) этого множества входит в него вместе со своей малой окрестностью.
Определение 3.3. Если каждая граничная точка множества {M} является точкой этого множества, то множество {M} называется замкнутым.
Определение 3.4. Множество {M} пространства Еm называется связным, если две любые его точки можно соединить непрерывной кривой, все точки которой принадлежат этому множеству.
Определение 3.5. Открытое и связное множество {M} в пространстве Еm называется областью.
Приведем некоторые примеры множеств {M} точек евклидова плоскости и пространства.
1.(x-a)2+(y-b)2≤R2 - множество {M} точек евклидовой плоскости, называемой кругом радиуса R с центром в точке M0(a;b).
2.(x-a)2+(y-b)2<R2 - множество {М} точек евклидовой плоскости, казывается открытым кругом радиуса R - с центром в точке M0(a;b).
3.(x-a)2+(y-b)2+(z-c)2≤R2 - множество {M} точек евклидова пространства, называемым шаром радиуса R с центром в точке
M0(a;b;c).
4.(x1-x10)+(x2-x20)2+...+(xm-xm0)2≤R2 или ρ(М;M0)≤R - множество
{M} точек m-мерного евклидова пространства, называемым m-мерным
щаром радиуса R с центром в точке M0(x10, x20,...,xm0).
5. ρ(М;M0)=R - множество {M} точек m-мерного евклидова пространства, называемым m-мерной сферой.
89

3.2. Предел функции нескольких переменных
Пусть функция f(M)=f(x,y,z) определена в окрестности точки M0(x0,y0,z0) трехмерного евклидова пространства, кроме, быть может, самой этой точки.
Определение 3.6. Число b называется пределом функции
f(M)=f(x,y,z) в точке M0(x0,y0,z0) ( lim f(M )= b ), если для любого ε>0
M →M 0
найдется δ>0 такое, что из неравенства 0<ρ(M,M0)<δ следует неравенство |f(M)-b|<ε, где ρ(M,M 0 )=  (x − x0 )2 +(y − y0 )2 +(z − z0 )2 есть расстояние от точки М до точки M0.
(x − x0 )2 +(y − y0 )2 +(z − z0 )2 есть расстояние от точки М до точки M0.
Заметим, что формально это определение совпадает с аналогичным определением предела функции одной независимой переменной. Однако, на самом деле это не так. Ведь здесь для существования предела ставится более жесткое требование. На самом деле, требуется, чтобы для любой последовательности точек М, стремящихся к М0 по произвольной кривой, существовал один и тот же предел.
Рассмотрим несколько примеров.
Пример 1. Пусть f(M )= f(x, y)= |
x2 |
− y2 |
. |
|||||||||||
x2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+ y2 |
||
Найдем |
lim |
|
f(M )= lim |
|
x2 |
− y2 |
, когда M→M0 по прямой y=kx. |
|||||||
|
|
|
|
|||||||||||
|
M →M 0 (0;0) |
|
|
|
x→0 x2 + y2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
y→0 |
|
|
|
|
|
||
Имеем |
lim |
x2 |
− y2 |
= |
|
1 − k2 |
. |
Но |
|
при разных k получим разные |
||||
|
+ y2 |
|
|
|||||||||||
|
x→0 x2 |
|
1 + k2 |
|
|
|
|
|
||||||
y→0
ответы, т.е. значение предела зависит от пути, по которому M→M0. Следовательно, предела от рассматриваемой функции не существует.
Пример 2. Пусть ϕ(M )= ϕ(x, y)= x3 + y3 . x2 + y2
Найдем |
|
lim |
= lim |
x3 + y3 |
. |
|
|
|
|
|
|
|
|||||||
x2 + y2 |
|
|
|
|
|
|
|
||||||||||||
|
|
M →M 0 (0;0) |
|
x→0 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
y→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как |
|
x3 + y3 |
|
|
≤ (x2 |
+ y2 )32 , то |
|
) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(x |
2 |
+ y |
2 |
32 |
1 |
|
||
|
|
|
|
|
|
ϕ(x, y) |
|
≤ |
|
|
|
= (x2 + y2 ) |
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||
|
|
|
|
|
|
|
|
x2 + y2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда
90
