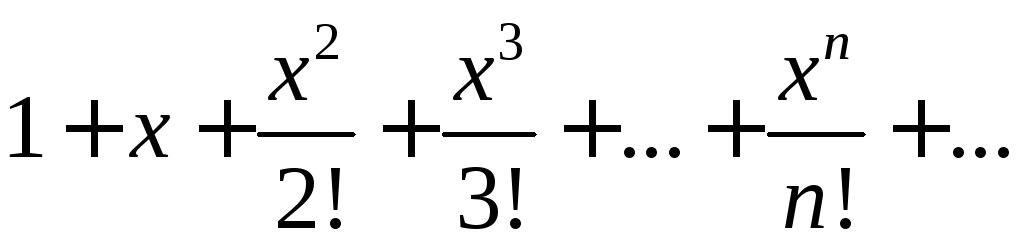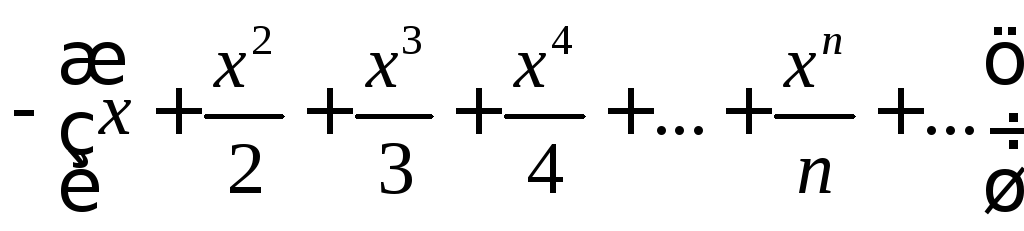- •9. Понятие интегралов на поверхности
- •9.1. Поверхностный интеграл первого рода
- •9.2. Понятие о двусторонней поверхности
- •9.3. Поверхностный интеграл второго рода
- •10. Элементы теории поля
- •10.1. Скалярное поле Производная по направлению. Градиент
- •10.2. Векторное поле
- •Свойства простейших векторных полей
- •11. Дифференциальные уравнения
- •11.1. Основные понятия
- •11.2. Виды и способы решения дифференциальных уравнений
- •12. Числовые и функциональные ряды
- •12.2.3. Стандартные числовые ряды с положительными членами
- •12.2.4. Достаточный признак сходимости знакопеременного ряда
- •12.2.5. Достаточный признак сходимости знакочередующихся рядов (теорема лейбница)
- •12.2.6. Абсолютная и условная сходимость знакопеременных рядов
- •12.3. Числовые ряды с комплексными членами
- •12.4. Функциональные и степенные ряды
- •12.4.1. Область сходимости. Интервал сходимости
- •12.4.2. Равномерная и неравномерная сходимость
- •Признак (Вейерштрасса) равномерной сходимости ряда
- •12.5. Ряды Тейлора
- •12.5.1. Необходимое условие разложения функции в ряд тейлора
- •12.5.2. Достаточное условие разложения функции в ряд тейлора
- •12.5.3. Ряд маклорена
- •12.5.4. Стандартные разложения функций в ряд маклорена
- •12.5.5. Примеры приближенных вычислений с помощью рядов
- •13. Ряды фурье
- •13.1. Достаточное условие разложения функции в ряд Фурье
- •13.2. Ряд Фурье для функции, заданной на отрезке
- •13.3. Ряды Фурье для четных и нечетных функций
12.5. Ряды Тейлора
12.5.1. Необходимое условие разложения функции в ряд тейлора
(по
степеням
![]() где
где![]() – фиксированная точка). Если непрерывная
функция
– фиксированная точка). Если непрерывная
функция![]() бесконечное число раз дифференцируема
в окрестности точки
бесконечное число раз дифференцируема
в окрестности точки![]() ,
то она может быть представлена в виде
ряда Тейлора:
,
то она может быть представлена в виде
ряда Тейлора:

12.5.2. Достаточное условие разложения функции в ряд тейлора
называется
достаточным
условием
сходимости ряда Тейлора
к порождающей его функции и заключается
в следующем. Чтобы ряд Тейлора сходился
к порождающей его функции
![]() т. е. сумма ряда Тейлора совпадала с
данной функцией:
т. е. сумма ряда Тейлора совпадала с
данной функцией:![]() достаточно, чтобы
достаточно, чтобы![]() где остаточный член
где остаточный член и
и![]() (форма Лагранжа).
(форма Лагранжа).
Пример.
Разложить в ряд Тейлора функцию
![]() по степеням
по степеням![]() .
.
Решение.
Запишем ряд Тейлора для данной функции
при
![]()

и
вычислим значения данной функции и ее
производных в точке
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
……………….. ……………….
![]()
![]()
Найденные
значения подставим в ряд Тейлора и
получим разложение данной функции по
степеням
![]() :
:

Исследуем сходимость этого ряда по признаку Даламбера:

Решая
последнее неравенство, находим интервал
![]()
Границы этого интервала исследуем особо.
Подставляя
в ряд
![]() ,
затем
,
затем![]() ,
получим числовые ряды
,
получим числовые ряды и
и![]() ,
которые расходятся, так как для каждого
из этих рядов
,
которые расходятся, так как для каждого
из этих рядов![]()
Следовательно,
интервал сходимости полученного ряда
Тейлора для функции
![]() есть промежуток
есть промежуток![]() .
.
Замечание.
Исследуя остаточный член
![]() формулы Тейлора, можно убедиться, что
полученный ряд сходится к данной функции
именно на указанном интервале.
формулы Тейлора, можно убедиться, что
полученный ряд сходится к данной функции
именно на указанном интервале.
12.5.3. Ряд маклорена
Если
![]() то ряд Тейлора называетсярядом
Маклорена
и разложение функции
то ряд Тейлора называетсярядом
Маклорена
и разложение функции
![]() в ряд Маклорена называетсяразложением
функции по степеням
х
и имеет следующий вид:
в ряд Маклорена называетсяразложением
функции по степеням
х
и имеет следующий вид:

Замечание.
Значение
функции
![]() и суммы ряда совпадают лишь в точках
области сходимости.
и суммы ряда совпадают лишь в точках
области сходимости.
12.5.4. Стандартные разложения функций в ряд маклорена
|
№№ п/п |
Функция |
Ряд Маклорена |
Интервал сходимости |
|
1. |
|
|
|
|
2. |
|
|
|
|
3. |
|
|
|
|
4. |
|
|
|
|
5. |
|
|
|
|
6. |
|
|
|
|
Биномиальный ряд | |||
|
7. |
|
|
|
|
8. |
|
|
|
|
9. |
|
|
|
12.5.5. Примеры приближенных вычислений с помощью рядов
Пример
13. Вычислить
значение
![]() точностью до 0,001.
точностью до 0,001.
Решение.
Ряд Маклорена для функции
![]() :
:
сходится
в интервале
![]() .
Полагая
.
Полагая![]() ,
получим:
,
получим:
![]()
Для
того чтобы выбрать необходимое число
членов полученного числового ряда для
вычисления значения е
с заданной
точностью, оценим остаток ряда
![]() при
при![]() .
.

Заметим, что все члены последнего ряда не превышают значений соответствующих членов ряда

представляющего
собой бесконечно убывающую геометрическую
прогрессию. Следовательно, по теореме
о сравнении знакоположительных рядов
![]() и ошибка, допускаемая при замене суммы
ряда частичной суммой, не превосходит
и ошибка, допускаемая при замене суммы
ряда частичной суммой, не превосходит![]() .
Учтем, что при
.
Учтем, что при![]() величина
величина![]() Значит, для вычисления
Значит, для вычисления![]() с точностью до 0,001 достаточно взять
сумму первых пяти членов ряда:
с точностью до 0,001 достаточно взять
сумму первых пяти членов ряда:![]()
Пример
14. Пользуясь
соответствующим рядом, вычислить
![]() с точностью до 0,001.
с точностью до 0,001.
Решение. Выполним следующее преобразование:

Применяя
биномиальный ряд и полагая
![]() ,
,![]() ,
получим:
,
получим:

Учитывая,
что в полученном
знакочередующемся ряде
значение четвертого члена меньше 0,001,
делаем вывод: для вычисления
![]() с заданной точностью достаточно взять
сумму трех первых членов ряда:
с заданной точностью достаточно взять
сумму трех первых членов ряда:![]()