11.2. Виды и способы решения дифференциальных уравнений
Название и вид дифференциального уравнения |
Способ решения |
|
1. Дифференциальные уравнения первого порядка |
||
1 |
2 |
3 |
1.1 |
Уравнение с разделяющимися переменными
|
Делим на произведение «лишних» множителей:
|
1.2 |
Однородное
|
Подстановка
|
1.3 |
Линейное
|
Подстановка
1)
2)
|
1.4 |
Уравнение Бернулли
|
Подстановка
1)
2)
|
2. Дифференциальные уравнения, допускающие понижения порядка |
||
2.1 |
|
Умножая обе части уравнения на dx и интегрируя n раз, получим общее решение
|
2.2 |
В явном виде не содержит у:
|
Подстановка
|
2.3 |
В явном виде не содержит х:
|
Подстановка
|
Продолжение таблицы
3. Однородные дифференциальные уравнения второго порядка с постоянными коэффициентами |
||
1 |
2 |
3 |
|
Характеристическое уравнение
|
а)
Корни характеристического уравнения
действительные и различные, то есть
Общее
решение:
б)
Корни характеристического уравнения
действительные и равные, то есть
тогда
в) Корни характеристического уравнения комплексные:
Частные линейно независимые решения уравнения:
Общее решение:
|
4. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами |
||
|
|
Общее
решение
где
|
4.1 |
|
где
|
,
следовательно, частные линейно
независимые решения:
значит общее
решение:
–
общее решение соответствующего
однородного уравнения;
–
какое-либо частное ре-шение неоднородного
уравнения
–
многочлен той же сте-пени,
что и
k
– кратность корня
в характеристическом уравненииОкончание таблицы
1 |
2 |
3 |
4.2 |
|
|
4.3 |
|
где
|
4.4 |
Правая часть дифференциального уравнения имеет общий вид:
|
Метод
вариации произвольных
постоянных.
Общее решение:
|
и
– многочлены
наивысшей степени среди степеней
многочленов
и
,
–
частное решение уравнения с правой
частью
–
частное
решение уравнения с правой частью
где
и
– частные,
линейно независимые ре-шения
соответствующего однород-ного
уравнения;
– функции,
определяемые из системы:
12. ЧИСЛОВЫЕ И ФУНКЦИОНАЛЬНЫЕ РЯДЫ
12.1. Виды рядов
1)
Если
где
то
–
называется числовым рядом.
2)
Если
где
то
– функциональный
ряд.
3)
Если
где
– фиксированная точка;
– числа,
то
– степенной
ряд.
4)
В случае, когда
степенной ряд принимает вид
12.2. Числовые ряды. Признаки сходимости числовых рядов
Числовые
ряды
Ряды
положительных членов
Знакопеременные
ряды
где
среди Un
есть как положительные, так и отрицательные
члены
где
Знакочередующие
ряды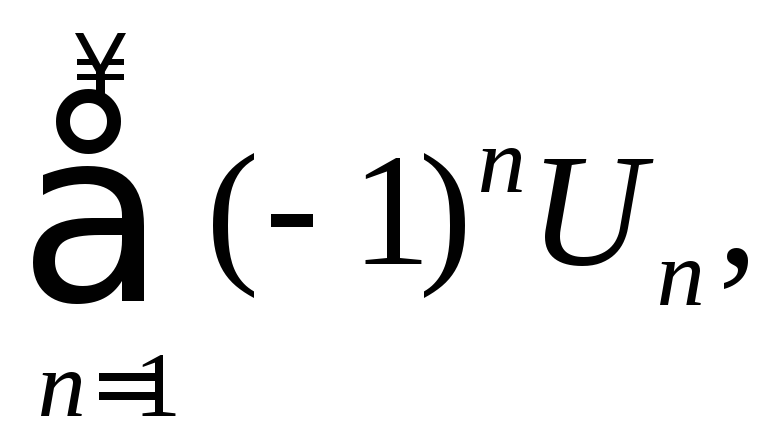
где
12.2.1. ПРИЗНАКИ СХОДИМОСТИ ЛЮБОГО ЧИСЛОВОГО РЯДА
Необходимый
признак.
Если ряд сходится, то
Следствие. Нарушение необходимого признака является достаточным признаком расходимости числового ряда:
если
то ряд расходится.
Достаточный
признак.
Если
то ряд сходится.
12.2.2. ДОСТАТОЧНЫЕ ПРИЗНАКИ СХОДИМОСТИ ЗНАКОПОЛОЖИТЕЛЬНЫХ РЯДОВ
1.
Признаки
сравнения.
Пусть
исследуемый ряд (неиз-вестного поведения
в смысле сходимости), а
– известный ряд.
1.1.
Если существует
то оба ряда либо сходятся, либо расходятся
одновременно.
1.2.
Если
начиная с некоторого номера n
и ряд (2) сходящийся, то сходится и ряд
(1).
1.3.
Если, начиная с некоторого номера n,
и ряд (2) расходящийся, то расходится и
ряд (1).
2. Признак Даламбера.
Если
существует
и если
3. Интегральный признак Коши.
Если
и
– функция монотонно убывающая, то ряд
сходится или расходится вместе с
несобственным интегралом
4. Радикальный признак Коши.
Если
существует
то
