3.3.1. Номинальная ставка
При начислении процентов несколько раз
в году можно воспользоваться формулой
(3.1). В этом случае nозначает число периодов начисления, аi– ставка за
соответствующий период. Пустьj– годовая ставка, аm– число периодов начисления в году.
Каждый раз проценты начисляются по
ставке
.
Ставкуjназывают
номинальной. Формула наращения:
, (3.7)
где
– общее число периодов начисления
процентов.
Пример 3.6.Изменим одно условие в примере 3.1. Пусть теперь проценты начисляются не один раз в году, а поквартально. В этом случаеN= 20. Найти сумму долга.
руб.
А при ежегодном начислении процентов мы получим
руб.
Чем чаще начисляются проценты, тем быстрее идет процесс наращения (цепной процесс). Например:
|
m |
1 |
2 |
4 |
12 |
365 |
|
Множитель наращения |
6,1917 |
6,7275 |
7,04 |
7,2682 |
7,385 |
Пример 3.7.Какова сумма долга через 25 месяцев, если его первоначальная величина500 тыс. руб., проценты сложные, ставка 20 % годовых, начисление поквартальное?
По условиям задачи число периодов наращения N= 25 : 3 = 8⅓. Применим два метода наращения: общий и смешанный.
1. Общий метод:
руб.
2. Смешанный метод:
руб. [10, с.
49–51].
3.3.2. Эффективная ставка
Другое название – действительная
ставка. Она измеряет тот реальный
относительный доход, который получают
в целом за год. Иначе говоря, эффективная
ставка – это годовая ставка сложных
процентов, которая дает тот же результат,
что и m-разовое
начисление процентов по ставке
.
Обозначим эффективную ставку через i. По определению множители наращения по двум ставкам (эффективной ставке и номинальной ставке приm-кратном начислении процентов) должны быть равны друг другу:
.
Отсюда следует:
. (3.8)
При m>1 эффективная ставка больше номинальной.
Если в договоре номинальная ставка jприm-кратном начислении процентов заменяется на эффективную ставкуi, то финансовые обязательства сторон договора не изменятся. Обе ставкиэквивалентны в финансовом отношении. Поэтому разные по величине номинальные ставки оказываются эквивалентными, если соответствующие им эффективные ставки одинаковы.
Пример 3.8.Найти размер эффективной ставки, если номинальная ставка равна 25 % при ежемесячном начислении процентов.
.
Для участвующих в сделке сторон безразлично, применить ставку 25 % при ежемесячном начислении процентов или годовую (эффективную) ставку 28,0732 %.
Введем обозначение j(m)– размер номинальной ставки и число начислений за год. Эквивалентная замена номинальной ставки имеет место только когда выполняется равенство:
.
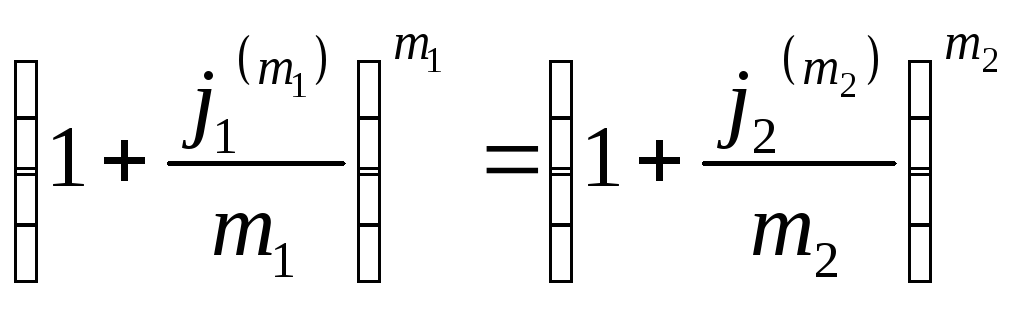Поскольку mможет принимать только целые значения, то удобнее определять значение новой ставки, задавшись величинойm2:
.
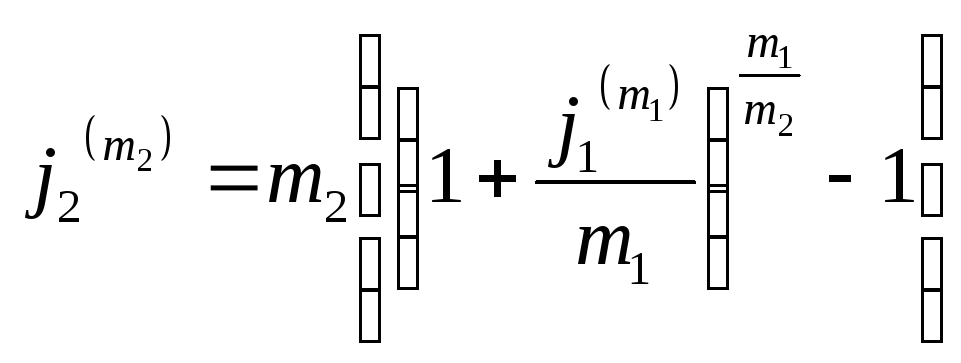Пример 3.9.Определить номинальную ставкуj(4), которая безубыточно заменяет ставкуj(12)= 25 % в примере 3.8.
.
Т. о., сокращение количества начислений потребует увеличения ставки с 25 % до 25,524 %.
При подготовке контрактов может возникать необходимость определенияjпо заданным значениямiиm [10, с. 51–53]:
. (3.9)