2010_03_КР ТеорМех

Полагая здесь t=1 с, найдем искомое перемещение х1.

Ответ: х1=0,33 м.

б) Определение ускорения а1.

Проделав те же рассуждения и выкладки, что и в предыдущем примере, получим уравнение (1) и формулу (2). Для определения а1 продифференцируем дважды по времени обе части равенства (2). Получим

Полагая здесь t=1с, определим искомое уравнение а1.

Ответ: а1=–2,51 м/с2. Знак минус указывает на то, что ускорение тележки направлено влево.

в) определение скорости u1. Чтобы определить u1, воспользуемся теоремой об изменении количества движении системы Q в проекции на ось х. Так как

Q D = m2 vD - количества движения тележки и груза D соответственно (u – скорость тележки, vD - скорость груза по отношению к осям Оху). Тогда из равенства (7) следует, что

Для определения vDx рассмотрим движение груза D как сложное, считая

его движение по отношению к тележке относительным (это движение, совершаемое при вращении стержня AD вокруг оси А), а движение самой тележки – переносным. Тогда vD = vDпер + vDотн и

vотнDx = -vDотн cosϕ . Окончательно из равенства (9) получим

41

xD = x − l sinϕ ; тогда vDx = x&D = x& − lϕ& cosϕ , где x& = ux , а ϕ& = 2πt 2 .)

При найденном значении vDx равенство (8), если учесть, что ux = u , примет вид

Постоянную интегрирования С1 определим по начальным условиям: при t=0 и u=0. Подстановка этих величин в уравнение (11) дает C1 = ( m1 + m2 )u0 и

тогда из (11) получим

Отсюда находим следующую зависимость скорости u тележки от времени:

Положив в уравнении (12) t=1с, определим искомую скорость u1.

Ответ: u1=– 0,76 м/с. Знак минус указывает, что скорость тележки направлена влево.

г) определение реакции N1. Для определения реакции N1 воспульзаемся теоремой о движении центра масс системы. Составим дифференциальное урав-

42

Подставив найденное выражение M&y&C в уравнение (8), получим зависимость N от t:

Задача Д3. Теорема об изменении кинетического момента системы.

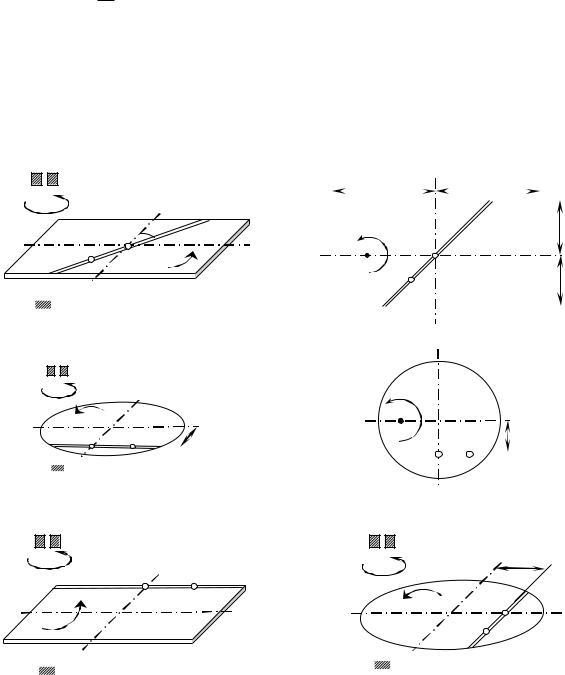
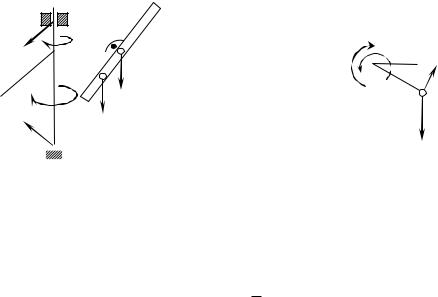
Условие. Однородная горизонтальная платформа (круглая радиуса R или прямоугольная со сторонами R и 2R, где R = 1,2 м) массой m1=24 кг вращается с угловой скоростью ω0=10 с-1 вокруг вертикальной оси z, отстоящей от центра масс С платформы на расстоянии ОС=b (рис. Д3.0 – Д3.9, табл. Д3); размеры для всех прямоугольных платформ показаны на рис. Д3.0а (вид сверху).

В момент времени t0=0 по желобу платформы, начинает двигаться (под действием внутренних сил) груз D массой m2=8 кг по закону s=AD=F(t), где s выражено в метрах, t – в секундах. Одновременно на платформы, изображённые на рис. 0–4, начинает действовать пара сил с моментом М (задан в ньютонметрах; при M<0 его направление противоположно показанному на рисунках); для платформ, изображенных на рис. 5–9, М = 0.

Определить: для платформ, изображенных на рис. 0–4, зависимость ω=f(t), т. е. угловую скорость платформы, как функцию времени; для платформ, изображенных на рис, 5–9 – угловую скорость ω1 платформы в момент времени

t1=1 с.

Форма желоба на рис. 0–4 прямолинейная (желоб КE), на рис. 5, 6, 7 – окружность радиуса R (обод платформы), на рис 8, 9 – окружность радиуса r = 0,5 R. На всех рисунках груз D показан в положении, при котором s>0 (когда s<0, груз находится по другую сторону от точки А); на рис. 5–9 расстояние s=АО отсчитывается по дуге окружности. Изображая чертеж решаемой задачи, провести ось z на заданном расстоянии ОС=b от центра С.

Указания. Задача Д3 – на применение теоремы об изменении кинетического момента системы. При применении теоремы к системе, состоящей из платформы и груза, кинетический момент Кz системы относительно оси z определяется как сумма моментов платформы и груза. При этом следует учесть, что абсолютная скорость v груза складывается геометрически из относительной vот и переносной vпер скоростей, т.е. v = vот + vпер . Поэтому и количество движения

этого груза mv = mvот + mvпер . Тогда можно воспользоваться теоремой Варинь-

она (статика), согласно которой mz ( mv ) = mz ( mvот ) + mz ( mvпер ) ; эти моменты вычисляются так же, как моменты сил. Подробнее ход решения для случая, когда надо ω=f(t), разъяснен в примере Д3.

В случае, когда М = 0 и надо определить ω1, воспользоваться законом сохранения кинетического момента (показав, что он здесь имеет место). При этом

43

следует сначала найти и показать на чертеже положения D0 и D1 груза в моменты времени t0=0 и t1=1c (найти, чему равен угол ACD при t0=0 и t1=1c), а также определить, чему равна и как направлена скорость vот в эти моменты времени. После этого, так же как в примере Д3, надо вычислить Кz, но не для произвольного момента времени, а сначала для момента t0=0 (когда груз в положении D0 и ω=ω0), а затем для момента t1=1c (когда груз в положении Dt и ω=ω1) и использовать закон сохранения Кz.

Момент инерции прямоугольной пластины с массой m и сторонами а1 и а2 относительно оси Сz, перпендикулярной пластине и проходящей через ее центр

масс С, равен 12m ( a12 + a22 ) .

При решении задачи полезно изобразить на вспомогательном чертеже вид на платформу сверху (с конца оси z), как это сделано в качестве примеров

44

Таблица Д3

45

Пример Д3. Горизонтальная трубка АВ массой m1 (рис. Д.6а) с помощью стержня ОС жестко скреплена с вертикальным валом ЕН, который вращается вокруг оси z с угловой скоростью ω0 (на рис. Д3.б показан вид сверху). В середине С трубки находится шар D массой m2. В момент времени t0=0 на вал начинает действовать вращающий момент М (момент относительно оси z) и одно-

временно шар начинает двигаться вдоль трубки по закону CD=s=f(t).

Дано: m1=15 кг; m2= 10 кг, АС= СВ=СО =l=1 м, ω0=2c-1, s=0,4t2 (s – в мет-

рах; t – в секундах), М=kt где k =6 Н∙м/с.

Определить: ω= f(t) —закон изменения угловой скорости трубки, пренебрегая массой стержня ОС и вала.

Решение. Рассмотрим механическую систему, состоящую из трубки АВ и шара D. Для определения ω применим теорему об изменении кинетического момента системы относительно оси z:

Изобразим действующие на систему внешние силы: силы тяжести Р1, Р2, реакции RЕ, RН и вращающий момент М. Так как силы Р1 и Р2, параллельны оси z, а реакции RЕ и RН эту ось пересекают, то их моменты относительно оси z равны нулю. Тогда, считая для момента положительны направление ω0 (т.е. против хода часовой, стрелки), получим åmz( Fke ) = −M = −kt и уравнение (1) примет та-

кой вид:

46

Умножая обе части этого уравнения на dt и интегрируя, получим

сительно оси z’ , параллельной оси z и проходящей через центр масс С трубки). Рассматривая трубку как однородный стержень длиной АВ=2l, получим