Ефимов А.Д. Физика

Среду проводника с поверхностной плотностью свободного заряда

′

Мак

σ0 обозначим индексом 1, среду диэлектрика индексом 2, рис. 22.

Тогда в соответствии с (69) и с уче-

N

2-

òîì E1

= D1

= 0 имеем D2n

= σ0,

1-

где вектор n направлен из проводни-

′Ðèñ. 22:

ка в диэлектрик. В диэлектрике по-

ле будет равно E2n

.

= D2n/(εε0) =

σ0/(εε0). Òàê êàê E2n = (σ0 + σ )/ε0,

òî σ0 + σ

= σ0/ε, связанный заряд равен

.О

−

0

ε

σ′ =

ε − 1 σ .

С

(76)

адмирала

Данное соотношение находится в соответствии с формулой (60).

имени

Ф

Если через некоторую поверхность за время t переносится заряд q,

то говорят, что через эту поверхность течет ток

Мак

I =

d q

.

(77)

d t

.

Учитывая, что носителями тока, например в растворах, могут

.О

быть как положительные, так и отрицательные заряды

d q

d q+

d q−

С

I =

=

+

.

(78)

d t

d t

d t

Скорость заряженных частиц, как и их концентрация в отдель-

женных носителей,адjмиралявляется точечнойахарактеристикой, показы-

ных точках поверхности S, может быть различна, поэтому ток I

рассматривается как скалярная величина, хотя направление тока

на рисунках и схемах указывается и это направление соответствует

движению положительно заряженных частиц. Если площадь по-

верхности настолько мала, что на всем ее протяжении концентра-

ция и скорости носителей тока неизменны, то в этом случае вели-

÷èíó dI можно воспринимать как вектор, а величина

j =

d I

(79)

d S

носит название плотности тока, S площадь поверхности S, íîð-

имени

маль к которой ориентирована по скоростям положительно заря-

вающей, какой ток течет через единичную поверхность. Ток через

конечную поверхность S находится как

I = ZS (j(S), dS)

(80)

Ф

(обозначение j(S) предполагает, что плотность тока является функ-

цией точки поверхности).

IS (j(S), dS) = −dt ZV ρ dV.

Мак

d

R R

R

H

Так как объем V и ограничивающая его поверхность фиксиро-

âàíû, òî

d V ρ dV /dt =

V

∂ρ/∂t dV

и в силу теоремы Гаусса

S (j, dS) =

V divj dV , а потому

.

∂ρ

.О

ZV divj dV = −ZV ∂t dV,

С

здесь объем можно взять произвольно малым, что приводит к урав-

нению

Обобщая этот результат

адмиралана носители зарядов разных знаков, полу-

divj = −

∂ρ

∂t

,

(81)

которое называется уравнением непрерывности в дифференциаль-

ной форме.

Пусть имеются только положительные но-

UT

сители заряда

e+

с концентрацией n+ è ñêî-

S

+.

ростью их перемещения в пространстве u

Тогда в соответствии с рис. 23 за время t ÷å-

рез площадку площадью

S пройдет заряд

Ðèñ. 23:

q = e+n+ Su+t, соответственно ток будет

I = q/t = e+n+

Su+, а плотность тока j

= I/ S = e+n+u+.

имени

÷èì

j = e+n+u+ + e−n−u−,

(82)

здесь e− < 0. Используя объемную плотность зарядов ρ± = e±n±,

получим

Ф

j = ρ+u+ + ρ−u−.

(83)

6.1 Закон Ома для участка цепи

I =

1

U.

(84)

R

Это закон Ома для участка цепи. Размерность R принята за Ом,

[R] =Îì.

Мак

.

Очевидно, что чем длиннее проводник, тем больше будет сопро-

тивление и во сколько раз площадь сечения проводника будет боль-

ше, тем меньше будет R. Это позволяет ввести понятие.Оудельного

сопротивления проводника ρ, которое уже не будет зависеть от гео-

метрии последнего. В зависимости от того, неизменна ли площадь

С

сечения проводника на всем его протяжении или меняется, будут и

соответствующие выражения для сопротивления

l

l2

dl

; R = Zl1

R = ρ

ρ S(l) .

(85)

S

Величина

σ = 1

ρ

(86)

носит название удельной проводимости.

Рассмотрим уравнения (84) и (85) для случая малого цилиндра

с характеристиками S,

l, тогда I = j S, U = E l, R = ρ

l/ S

и соответственно

адмирала

E = jρ èëè j = σE,

(87)

что носит названние закона Ома в дифференциальной форме.

6.2 Закон Ома для неоднородного участка цепи

имени

Ф

Под неоднородным участком цепи понимается участок, где помимо

потенциальной силы qE на заряд действует сила, не являющаяся

Пусть по однородному участку цепи с сопротивлением R течет ток

I, напряжение на нем U = IR. Смысл U разность потенциальных

энергий единичного заряда между точками на концах участка. Ес-

ли через участок проходит заряд q, то работа, совершаемая при

прохождении этого участка зарядом A = U q. Òàê êàê q = It, òî

A = U It, что приводит к тому, что теплота, выделяемая на участке

за время t

Мак

Q = RI2t,

.(90)

которое носит название закона Джоуля-Ленца (для участка цепи).

Этот закон был определен экспериментально. При этом соответ-

ственно мощность

.О

С

P = U I = RI2 =

U 2

.

(91)

R

За время dt на участке dl выделяется количество теплоты

dQ = dR I2 dt = ρdl (jdS)2dt = ρj2dV dt,

dS

dV = dSdl элемент объема участка цепи.

Удельная теплота или удельная мощность, т.е. мощность, при-

ходящаяся на единицу объема Póä = dQ/(dV dt) = ρj2. С учетом

закона Ома в дифференциальной форме j = σ(E + E ) получаем

Póä = ρj2 = j(E + E ) = σ(E + E )2.

(92)

Рассмотрим смысл э.д.с., ε. Полная мощность в замкнутой цепи

при наличии неоднородности P = I2(R + r), ò.å. P = εI = εdq/dt,

дмира ала

откуда ε = P dt/dq = dQ/dq è ò. î. ε есть работа по перемещению

единичного заряда (1 Кл в СИ) в замкнутой цепи. Эта величина

не зависит от сопротивления R, íî çàòî îò R зависит время, за

которое эта работа будет совершена. Действительно, так как t =

q/I = q(R + r)/ε, то время, за которое будет перенесен один кулон

t = (R + r)/ε. Это время пропорционально общему сопротивлению

t R + r.

имени

Ф

Данный6.4 Разветвленныераздел посвящен доказательствуцепи. ПравилаправилКирхгофаКирхгофа, кото-

Ik (âõîä) =

Ik (выход).

(93)

k

k

X

X

I2

Для рис. 25 это будет соответствовать Мак

I3

I1 + I2 + I4 = I3 + I5.

.

I1

I4

I5

Если в схеме имеется N узлов, то незави-

.О

Ðèñ. 25:

симых уравнений такого рода будет N − 1.

Выделим произвольный замкнутый контур,

С

имеющий для определенности четыре узла, четыре неоднородных

элемента и соответствующие сопротивления, как это указано на

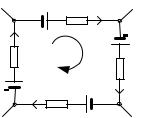
рис. 26. Распишем соотношение (88) для каждого из рассматри-

ваемых участков

I1(R1 + r1) = ϕ1 − ϕ2 + ε1

I2(R2 + r2) = ϕ2 − ϕ3 + ε2

I3(R3 + r3) = ϕ3 − ϕ4 + ε3

I4(R4 + r4) = ϕ4 − ϕ1 + ε4.

Складывая эти уравнения, получим, что потенциалы ϕi сокра-

щаются и

адмирала

k

Ik (Rk + rk ) =

εk .

(94)

k

X

X

В этом соотношении предполагается, что каждый из токов Ik

совпадает с общим обходом контура (на рис. 26 это по часовой

стрелке и обозначено буквой I). В том же случае, если направление

тока Ik не совпадает с общим направлением, то соответствующий

член в сумму должен входить со знаком минус. В правой стороне

имени

Ф

уравнения (94) предполагается, что все εk увеличивают потенциал

δIk ,I = 1, если выбранные направления Ik è I не совпадают;

δεk ,I = 0, åñëè εk увеличивает потенциал в направлении I;

δεk ,I = 1 åñëè εk уменьшает потенциал в направлении I.

Используя эти обозначения, запишем соотношение (94) в виде

(−1)δIk ,I Ik (Rk + rk ) =

(−1)δεk ,I εk .

(95)

k

k

Мак

X

X

Число независимых уравнений та-

ε1

, r1

R

кого рода для схемы будет на еди-

-

+

1

I1

1

2.

ницу меньше числа различных кон-

I4

ε2 , r2

+

туров. Соотношения (93) и (95) на-

R4

.ОI

зываются соответственно первым и

+

ε4 , r4R

R2

вторым правилом Кирхгофа.

ε3 , r3

I2

4

I

3

4

3

С

-+

Ðèñ. 26:

6.5

Эквивалентные цепи

Для упрощения анализа сложных электрических цепей отдельные

их участки, не содержащие ЭДС, можно заменить одним эквива-

лентным сопротивлением. Под эквивалентным понимают такое со-

противление, которое, будучи включенным в цепь вместо заменя-

емой группы сопротивлений, не изменяет распределение токов и

напряжений в остальнойадмиралачасти цепи.

При последовательном или параллельном соединении сопротив-

лений эквивалентные сопротивления соответственно определяются

выражениями

n

n

¢

−1

R =

Ri è

R =

−1

.

Ri

i=1

i=1

X

¡X

При анализе сложных схем встречаются случаи, когда часть схе-

имени

Ф

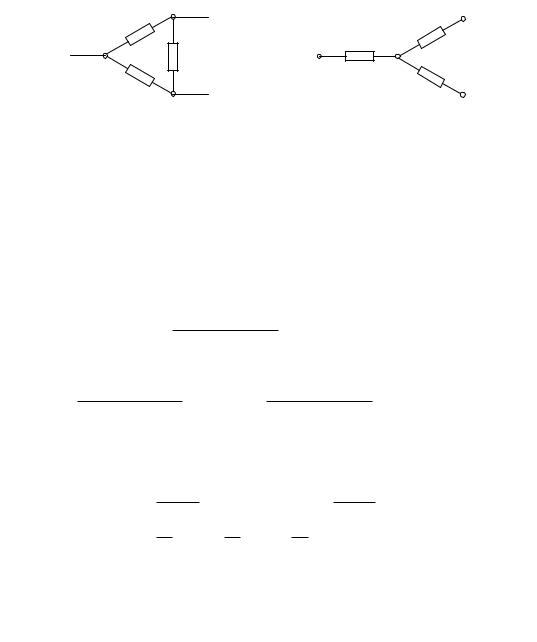
мы образует так называемый треугольник сопротивлений, рис. 27.

Схема упрощается, если треугольник с сопротивлениями Rab, Rbc,

Rca заменить эквивалентной звездой (рис. 28) с сопротивлениями

Ra, Rb, Rc. Иногда необходимо обратное преобразование звезды