Ефимов А.Д. Физика

2ε0

r

äëÿ r < R

E =

ρ

(31)

2

Мак

R ρ 1

2ε0

r

äëÿ r > R.

Таким образом, внутри цилиндра напряженность растет линей-

но с расстоянием от оси цилиндра, снаружи же цилиндра напря-

женность падает обратно пропорционально этому расстоянию.

Потенциал для бесконечной нити, как и в случае с бесконеч-

ной плоскостью, не имеет смысла, но разность потенциалов смысл

.О

имеет. Интегрируя выражение (30) в соответствии с (13), получаем

λ

r2

С

ϕ1 − ϕ2 =

ln

.

(32)

2πε0

r1

3.

Заряженная сфера и шар.

Рассмотрим сначала заряженную сферу с радиусом R и зарядом

Q. Находясь внутри сферы на расстоянии r от центра, из соображе-

ния симметрии очевидно, что если напряженность имеется, то она

должна быть направлена по радиусу, т.е. EkdS для каждой

точки

2

E.

мысленной сферы. Тогда поток через эту сферу будет равен 4πr

Заряд при этом внутри нее отсутствует, так как находится на ре-

альной сфере большего радиуса. Исходя из этого E = 0 для всех

точек внутри сферы. Для точек вне, поток имеет то же выражение

4πr2E, и в соответствии с теоремой Гаусса 4πr2E = Q/ε0, откуда

уже для всех точек

адмирала

E(r) =

0 äëÿ r < R

(33)

Q

1

r > R.

2 äëÿ

4πε0 r

В отличии от предыдущих случаев можно написать выражение

для потенциала

имени

Q

1

Ф

äëÿ r < R

ϕ(r) =

4πε0

R

(34)

Q 1

4πε0 r äëÿ r > R.

Q

Мак

r äëÿ r < R

E(r) =

.(35)

Q 1

4πε0 r2 äëÿ r > R,

.О

потенциал же

Q

Q

1

8πε0R3 (R2 − r2) +

4πε0

R äëÿСr < R

(36)

ϕ(r) =

Q 1

4πε0 r äëÿ r > R.

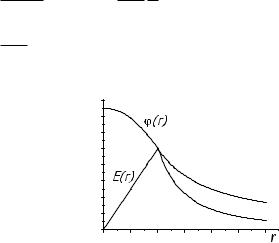
Зависимости

E(r)

è ϕ(r) для равномер-

но заряженного шара

приведены на рис. 11,

где в силу непрерыв-

ности E(r) ïðè r = R

производная ϕ(r) ïî

r ïðè r = R также

непрерывна.

адмирала

Следует обратить

внимание, что как для

заряженной сферы, так

и для шара напряжен-

Ðèñ. 11:

ность электрического

поля снаружи тождественна напряженности точечного заряда, по-

мещенного в центр. Внутри же для сферы напряженность равна

имени

Ф

нулю, а для шара растет линейно с радиусом.

Результаты данного раздела были получены на основе теоремы

Гаусса. Их можно получить и из дифференциального уравнения

(24), divE = ρ/ε0, что по существу есть также теорема Гаусса, но

E = f (r)(xi + yj + zk)

Мак

как внутри, так и снаружи шара. Кроме того очевидно, что в центре

шара напряженность равна нулю, т.е. E(0) = 0. Далее

divE(r)

=

∂

f (r)x +

∂

f (r)y +

∂

f (r)z =

∂z

∂x

∂y

.

= f ′(r)µ ∂x x + ∂y y + ∂z z¶ + 3f (r);

∂r

∂r

∂r

С

∂r

=

∂

(x2 + y2

+ z2)1/2 =

x

;

∂r

=

x

;

∂r

=

z

;

∂x

∂x

r

∂y

r

∂z.Оr

divE(r)

=

f ′(r)r + 3f (r) = ρ/ε0.

адмирала

Таким образом, мы получили обыкновенное дифференциаль-

ное линейное уравнение первого порядка относительно функции

f (r). Представляем ее в виде произведения двух функций, f (r) =

u(r)v(r), ÷òî äàåò

(u′v + v′u)r + 3uv = ρ/ε0.

Функция v(r) находится из условия v′(r)r + 3v(r) = 0. Îäíî èç

решений этого уравнения (

dv(r)/dr = −3dr/r; ln v(r) = ln r

−3) åñòü

v(r) = r−3.

После этого остается найти функцию u(r). После определения

v(r), имеем u′(r)r−3r = ρ/ε0,

u′(r) = ρ/ε0r2. Общее решение этого

имени

уравнения u(r) = ρ/ε0r3/3 + C. Таким образом,

1

C

f (r) =

3

ρ/ε0

+ r3 .

(37)

Внутри шара C = 0, òàê êàê E(0) = 0 è

E(r) =

ρ

(xi + yi + zk) =

ρ r.

Ф

3ε0

3ε0

Снаружи шара ρ = 0, исходя из (37)

Полученные результаты позволяют решать широкий круг задач.

Подытожим эти резудьтаты.

1. Внутри проводника нет объемных зарядов, все заряды кон-

Мак

центрируются на поверхности независимо от общего заряда и по-

тенциала проводника, причем в непосредственной близости от про-

водника E = σ/ε0, E k dS, где E есть именно полное поле,

создаваемое как зарядом на проводнике, так и системой

зарядов вне его.

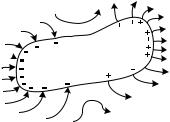
если же σ < 0, то вектор E направлен к поверхности проводника,.íî

.О

Если σ > 0, то вектор E направлен от поверхности проводника,

всегда перпендикулярно к линии поверхности, как это представлено

íà ðèñ. 12.

С

В связи с соотношением (38) может возникнуть ошибочное за-

ключение, что E вблизи проводника зависит только от локальной

адмирала

плотности σ заряда. Это не так. Напряженность E, êàê è ñàìî çíà-

чение σ, определяется всеми зарядами рассматриваемой системы.

2. Напряженность электриче-

ского поля внутри проводника рав-

íà íóëþ.

3. Все точки проводника име-

ют одинаковый потенциал. Это поз-

воляет решать задачи определе-

ния электрического поля вне про-

водников, имитируя с помощью несу-

ществующих зарядов эквипотен-

циальные поверхности.

Ðèñ. 12:

имени

Рассмотрим особенности электрического поля у острых краев

проводника. Пусть у нас имеются две металлические сферы с силь-

но различающими радиусами r1

r2, рис. 13. Соединим их тонкой

проволокой и зарядим эту систему, в результате чего на первой

сфере будет заряд Q, на второй q. Обе сферы будут иметь одинако-

вые потенциалы, что приводит к соотношению между ними Q/r1 =

Ф

q/r2. Тогда напряженности непосредственно у поверхности первой

и второй сфер будут относиться как E

1

/E

2

= (Q/r2)/(q/r2) = r

2

/r .

1

2

1

Следовательно, у сильно заостренных краев проводника возникает

чрезвычайно сильное поле, и ионы, оказавшиеся в этих местах, бу-

дут испытывать ускорение, приводящее к ионизации нейтральных

Мак

молекул. Процесс повторяется уже на новообразованных ионах. Имен-

но поэтому мы слышим постоянное гудение под высоковольтными

линиями электропередач. Неровности на проводниках возникают и

в силу загрязнения проводов. По тем же причинам возникает явле-

ние, называемое Огни святого Эльма разряд в форме светящихся

.

.О

пучков или кисточек, который появляется на острых концах высо-

ких предметов (башни, мачты, одиноко стоящие деревья, острые

вершины скал и т. п.) при большой напряженности электрического

С

поля в атмосфере. Они образуются в моменты, когда напряжен-

ность электрического поля в атмосфере у острия достигает вели-

чины порядка 500 В/м и выше, что чаще всего бывает во время

адмиралаC = ,

(39)

грозы или при ее приближении.

Рассмотрим уединенный проводник

R1

(проводник, внешнее поле по отношению

R

2

к которому отсутствует). При зарядке

проводника каждая новая порция заря-

да распределяется пропорционально преды-

дущей порции по поверхности провод-

Ðèñ. 13:

ника, поэтому его потенциал будет пря-

мо пропорционален его заряду или q = Cϕ, где C емкость про-

водника

(E, dl) = 4πε0

ZR r2 dr = 4πε0 R ,

(40)

имениϕ(R) = ZR

q

ϕ

ýòî

заряд, на который надо зарядить проводник, чтобы его

потенциал изменился на 1 В. Размерностью C является фарад

(Ô=Êë/Â).

Найдем выражения для емкости металлического шара и плос-

кого конденсатора. Пусть радиус шара R, то в соответствии с (14)

Ф

∞

1

∞ q

1 q

ε0S

Мак

C =

.

(41)

d

Таким образом, емкость плоского конденсатора прямо пропор-

циональна площади конденсатора и обратно пропорциональна рас-

стоянию между пластинами. При параллельном соединении кон-

.

.О

денсаторов происходит эффективное увеличение площади, поэто-

ìó C = C1 + C2. При последовательном соединении конденсаторов

происходит эффективное увеличение зазора между пластинами, по-

С

этому 1/C = 1/C1 + 1/C2 èëè C = C1C2/(C1 + C2).

W = 2 µΦ1(rадмирала2)q2 + Φ1(r3)q3 + Φ2(r1)q1 + Φ2(r3)q3 +

3 Энергия системы заряженных частиц и

проводника

Пусть мы имеем систему простых заряженных частиц. Под про-

стой частицей будем понимать ту, которую уже нельзя разделить

на составляющие части. Это приводит к отсутствию самовзаимо-

действия, то есть поле, создаваемое зарядом, не может взаимодей-

ствовать с этим же зарядом. Рассмотрим потенциальную энергию

взаимодействия трех зарядов. Пусть Φi(rj ) потенциал, создавае-

ìûé i-м зарядом в точке, определяемой радиус-вектором rj . Тогда

энергия взаимодействия равна

имени

1

+Φ3(r1)q1 + Φ3(r2)q2¶.

В этом выражении множитель 1/2 возникает из-за того, что

взаимодействие, например, первой частицы со второй учитывает-

ся дважды, это Φ1(r2)q2

è Φ2(r1)q1. Перекомбинируя написанное

Ф

выражение, получим

+ Φ3(r1))q1 + (Φ1(r2) + Φ3(r2))q2 +

W = 2 µ(Φ2(r1)

1

µϕ1(r1)q1 + ϕ2(r2)q2 + ϕ3

¶,

(Φ1(r3) + Φ2(r3))q3¶ =

1

(r3)q3

2

ãäå ϕ1(r1) потенциал, создаваемый в месте нахождения q1 çàðÿ-

да всеми остальными зарядами системы. В последнем выражении

символ (r1) является избыточным, поэтому уже для произвольного

числа частиц

X

Мак

1

W =

ϕiqi.

(42)

2

i

.

Перейдем к проводнику. Поскольку в проводнике потенциал во

i

= ϕ, òî

i

О

всех точках одинаков, т.е. ϕi

.

1

X

1

X

1

С

W = 2

ϕiqi = 2 ϕ

qi =

2 ϕq,

ãäå q полный заряд проводника. Используя понятие емкости про-

адмирала

водника (39), получаем

W =

1

ϕq =

q2

= Cϕ2 .

(43)

2

2C

2

Продемонстрируем полученный результат на примере заряжен-

ного плоского конденсатора. Каждая из пластин имеет заряды со-

ответственно q, −q и потенциалы ϕ1

и ϕ2. Это позволяет написать

выражение для энергии взаимодействия пластин

1

1

1

1

W =

(qϕ1

+ (−qϕ2)) =

q(ϕ1

− ϕ2) =

2 qU =

CU 2,

2

2

2

имени

ãäå U напряжение между пластинами, U = q/C. Учитывая выра-

2

d/(2ε0S). Это позволяет найти

жение для C (41), получаем W = q

силу притяжения между пластинами F = −∂W/∂d = −q2/(2ε0S).

4

Энергия электрического поля

Получим выражение энергии электрического поля для случая плос-

Ф

кого конденсатора. Энергия заряженного плоского конденсатора

равна CU 2/2, подставляя сюда выражение для C èç (41) è U = Ed,

получаем

CU 2

ε0SE2d2

ε0E2

W =

=

=

Sd,

2

2d

2

w =

W

=

ε0

E2.

(44)

2

V

Данное выражение может привести к вопросам, в чем прояв-

ляется эта энергия, и что является ее носителем. Для ответа на

эти вопросы рассмотрим электрическую энергию равномерно за-

Мак

ряженной сферы. Так как внутри равномерно заряженной сферы

напряженность равна нулю, то

.

ε0

q2

∞ 4πr2

1 q2 1

W = ZV wdV =

ZR

dr =

.О

2

(4πε0)2

r4

2

4πε0

R

Для элемента объема использовано выражение dV = 4πr2dr.

С

Полученный результат можно трактовать таким образом, что если

пропадут силы, удерживающие сферу как твердое тело, то под воз-

действием электрических сил отталкивания все заряды, имеющиеся

на сфере, разлетятся, и кинетическая энергия осколков будет равна

именно этой энергии. Интересно, что в отношении отдельно взятого

электрона такой расчет неприемлем. Радиус электрона R = 0 èëè,

по крайней мере, эксперименты не свидетельствуют о наличии у

электрона размера, поэтому соответствующий интеграл будет рас-

ходящимся, но электрон не может разделиться на составляющие, а

потому эта бесконечная энергия не может никак реализоваться, то

есть ее просто как бы и нет.

адмирала

5 Диэлектрики

Под диэлектриком или изолятором понимают вещество, практиче-

ски не проводящее электрического тока. Диэлектрики могут состо-

ять как из нейтральных молекул, которые в свою очередь могут

быть либо полярными, либо неполярными, так и из разноименных

ионов, находящихся в узлах кристаллической решетки, например,

Na Cl. Электрические свойства диэлектриков были проявлены че-

имени

Ф

конденсатор с помощью напряжения U0 до заряда Q0 = C0U0, затем

что напряжение на обкладках конденсатора уменьшается в некото-

рое число ε, зависящее от используемого вещества, U = U0

/ε. Òàê

как заряд на конденсаторе остался тем же, то Q0 = C0U0 = CU ,

поэтому C = C0ε. То есть емкость конденсатора увеличивается в

ε раз. Эта величина называется диэлектрической проницаемостью

вещества. Для всех веществ ε > 1, для вакуума ε = 1. Òàê êàê

напряженность в присутствии диэлектрика уменьшается, а напря-

женность, например для плоского конденсатора связана с напря-

жением соотношением E = U/d, то имеем

Мак

E = E0/ε,

.

.О

(45)

ãäå E0 поле свободных или сторонних зарядов.

Что же происходит с диэлектриком под действием поля сто-

ронних зарядов? Так как диэлектрик представляет собой систему

С

связанных зарядов, то при наличии внешнего поля они начинают

лишь смещаться: положительные по полю, отрицательные против

поля. Этот эффект называется поляризацией. Механизм образова-

ния смещенных зарядов связан с конкретным строением диэлектри-

ка. Если молекулы, не обладают электрическим дипольным момен-

том, то они называются неполярными. К ним относятся инертные

ãàçû He, Ar, Kr..., а также молекулы типа N2, O2, Cl2

, .... Ïîä äåé-

ствием электрического поля ядра молекул смещаются по направ-

лению поля, электроны против. В результате при включении поля

практически мгновенно неполярная молекула обретает дипольный

момент, ориентированный строго по полю. Аналогичный эффект

имеет место в диэлектрических кристаллах типа NaCl.

Молекулы, обладающие электрическим дипольным моментом,

адмирала

называются полярными. К ним относятся молекулы NO, CO2 è â

особенности молекулы воды H2O, обладающие значительным ди-

польным моментом. При отсутствии внешнего поля дипольные мо-

менты таких молекул вследствие теплового движения ориентирова-

ны хаотично, компенсируя друг друга. При включении поля возни-

кает преимущественная ориентация диполей в направлении поля.

Время такого выстраивания после включения поля зависит как от

значения дипольного момента, так и от значения момента инерции

имени

Ф

молекулы. Указанное явление полезно иметь ввиду для правильно-

го понимания диэлектрических свойств вещества при распростра-

нении электромагнитных волн в нем.

Для обычных веществ значения ε меняются в пределах от еди-