Ефимов А.Д. Физика

ϕ(r) = Zr∞(E, dl).

(14)

I (E, dl) = 0.

(15)Мак

Из (13) следует, что циркуляция E, определяемая кулоновским

полем, равна нулю

.

.О

Сделаем здесь еще одно замечание. Из математики известно,

правлен по нормали к эквипотенциальнойСповерхности по-

что градиент любой скалярной функции направлен по нормали к

поверхности, на которой функция неизменна. Такая поверхность

называется эквипотенциальной. Это значит, что вектор E íà-

тенциала ϕ.

адмиралаp = ql.

(16)

1.5 Поле электрического диполя

Под электрическим диполем понимают систему двух

равных по величине и противоположных по знаку

L

точечных электрических зарядов q, разнесенных в

пространстве на l = 2a, где вектор дает направ-

Ðèñ. 3:

ление от отрицательного заряда к положительному,

как это представлено на рис. 3. Под дипольным моментом данной

системы будем понимать выражение

имени

Сразу оговоримся, что нас интересует поле в точках, находя-

щихся на расстоянии от диполя, существенно превышающем разме-

ры самого диполя. С учетом этого получим выражение для потен-

циала в произвольной точке пространства. В соответствии с рис.

4 r, r+ è r− есть расстояния от центра диполя до рассматрива-

емой точки и соответственно от положительного и отрицательно-

го зарядов. Угол ϑ есть угол между вектором r è a èëè l. Ïî-

лучим приближенные выражения для r+ è r− через r è ϑ. Òàê

√

2 и раскладывая

r

2

2

, пренебрегая членом

Ф r+ =

+ a − 2ra cos ϑ

√

a

, ìû

приближенно корень в ряд с учетом того, что

1 ± x ≈ 1 ±x/2

E

α

Мак

r-

r+

r

-Q

ϑ

Q

-a

a

Ðèñ. 4:

.

.О

Выражение для потенциала есть

ϕ(r) =

1

(

q

q

) =

q

(r− − r+)

.

4πε0

r+

− r−

4πε0

r+r−С

2

Отбрасывая малый член a2 в выражении r+r− = r2 − (a, er )2 ≈

r

, и с учетом того, что r−−r+ = 2(a, er ) = (l, er ), а также с учетом

выражения (16) и (p, er ) = p cos ϑ

1

p cos ϑ

1

(p, r)

ϕ(r) =

=

r3 .

(17)

4πε0

r2

4πε0

Данное выражение определяет потенциал диполя в произволь-

ной точке пространства, радиус вектор r есть вектор, проведенный

от диполя до рассматриваемой точки.

Чтобы рассчитать напряженность поля, необходимо рассчитать

градиент выражения (17)

дмира ала

∂ pxx + py y + pz z

px

(p, r) 3

4πε0Ex = −

= −r3 −

(−

)2x =

∂x

(x2 + y2 + z2)3/2

r5

2

px

3(p, r)

= −

+

x.

r3

r5

Аналогично

имени4πε0Ey = −

py

3(p, r)

pz

3(p, r)

+

y;

4πε0Ez = −

+

z.

r3

r5

r3

r5

Ф

Это приводит к выражению

1

p

3(p, r)

E =

½−

+

r¾.

(18)

4πε0

r3

r5

Для удобства приведем несколько удобных формул. Значение

напряженности в произвольной точке будет определяться выраже-

íèåì

1

p

E = 4πε0 r3 p1 + 3 cos2 ϑ.

(19)

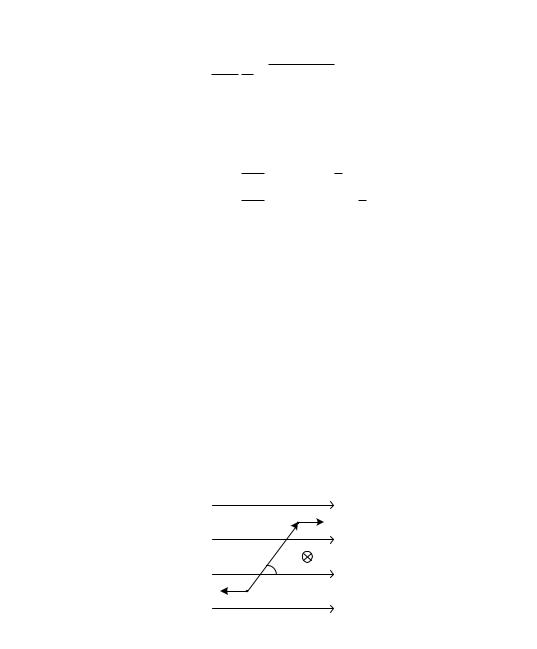
Направление же напряженности, отсчитанное от направления

диполя (рис. 4), будет определяться выражением

Мак

tg ϑ

π

.

α =

.О

ϑ + arctg(

2 ), äëÿ ϑ ≤

2

π ,

(20)

ϑ + arctg( tg ϑ ) + π, äëÿ ϑ >

2

2

ãäå óãîë ϑ есть угол между направлением диполя и прямой, со-

С

единяющей диполь с рассматриваемой точкой, а угол α åñòü óãîë

между направлением диполя и напряженностью E в рассматрива-

емой точке.

1.6 Электрический диполь во внешнем электри-

ческом поле

Данный раздел важен и сам по себе и в силу того, что позволяет

объяснить явления, часто наблюдаемые каждым из нас.

Диполь, помещенный в электрическое поле, будет находиться

под действием пары сил. Рассмотрим рис. 5. На один заряд дей-

ствует сила qE, на другой −qE. Вводя угол α между направлением

внешнего поля E и диполем p, мы получаем, что указанные две

адмирала

силы приводят к моменту пары сил

имени

|M | = qEl sin α = pE sin α.

+q

F

E

α

M

Ф

F

-q

Ðèñ. 5:

Мак

.

Ðèñ. 6:

.О

адмирала

С

Из рис. 5 становится понятным, что

M = [p, E].

(21)

Получим выражение для потенциальной энергии диполя во внеш-

нем поле. Легче всего это сделать, сложив потенциальные энергии

каждого из зарядов диполя.

W = qϕ+ − qϕ− = q(ϕ+ − ϕ−) = −qEl cos α = −(p, E),

ãäå ϕ± есть значение потенциалов в точках расположения положи-

тельного и отрицательного зарядов диполя, α угол между напря-

женностью поля и диполем. Таким образом, выражение для потен-

циальной энергии диполя

имени

W = −(p, E).

(22)

Это выражение достаточно универсально и дает правильные

значения не только по отношению к ориентационной свободе, но

и по отношению к тому случаю, если поле неоднородно (вывод не

был связан с предположением однородности поля). Зависимость

Ф

(22) îò α представлена на рис. 6, что в совокупностью с (21) да-

ет, что устойчивое положение диполя будет таково, что он будет

(p, E) = (p, )E + (E, )p + [p, rot E] + [E, rot p].

Мак

Рассмотрим все слагаемые. Второе и четвертое слагаемые со-

держат частные производные по координатам от вектора диполя.

Вектор диполя p является постоянным вектором, поэтому данные

.

слагаемые отсутствуют. Третье слагаемое содержит ротор от век-

слагаемое тоже аннулируется. Остается только первое.Ослагаемое

òîðà E. Ротор есть поверхностная плотность циркуляции рассмат-

риваемого вектора, но мы уже убедились, что для кулоновского по-

С

ля циркуляция напряженности равна нулю. Следовательно третье

адмирала

F = (p, )E = (px

∂/∂x + py ∂/∂y + pz ∂/∂z)(Exi + Ey j + Ez k). (23)

Рассмотрим простой пример, демонстрирующий смысл для си-

лы, определяемой данным выражением. Пусть в начале координат

находится точечный положительный заряд, а диполь располагает-

ся на оси OX (рис. 7). В силу симметрии это приводит к тому, что

Ey = Ez = 0. Кроме того, учитывая невихревой характер поля, бу-

дут равны и частные производные ∂Ex/∂y = ∂Ex/∂z = 0. Поэтому

F = Fxi = px(∂Ex/∂x)i = p cos α(∂Ex/∂x)i.

Для устойчивого положения диполя

имени

P

α = 0

,

cos α = 1

, à

∂Ex/∂x < 0

, поэто-

q

α

му диполь, находящийся в устойчивом

ориентационном положении, будет втя-

Ðèñ. 7:

гиваться в область более сильного поля.

При произвольной ориентации диполь может испытывать силу в

сторону более слабого поля, т.е. отталкиваться, но при этом он бу-

дет и поворачиваться. Повернувшись по полю, диполь начнет втя-

гиваться в область более сильного поля. Такого рода явление мы

Ф

цию,посянаблюдаемсебекпроизвольноприобретаютнейтральны,с притяжениемнаэлектрилизованнойдипольныйно под действиеммаленькихмомент,поляориентированныйбумажек,расческеиспытывают.притягивающихБумажки,поляризапо полюсами--.

В этом случае они начинают движение в сторону расчески.

Пусть имеется векторное поле скоростей v, тогда через элемен-

тарную площадку S за одну секунду протечет объем жидкости,

равный v

S cos α, ãäå α есть угол между вектором в районе пло-

щадки и перпендикуляром к площадке. Если этот перпендикуляр

обозначить как n и ввести понятие вектора элементарной площад-

êè

S =

Sn, то рассмотренный объем можно представит как

(v,

S). Если площадь S конечна, то поток жидкости будет равен

поверхностному интегралу второго рода Φ =

Мак

S

(v, dS). По анало-

.

гии с этим вводится понятие потока любого

векторного поля, на-

R

пример, поток напряженности электрического поля. В дальнейшем

нас будет интересовать поток через замкнутую поверхность S, êî-

торый имеет вид

.О

С

ΦE = IS (E, dS).

В математике известна теорема Гаусса-Остроградского, которая

утверждает, что поток через замкнутую поверхность любого век-

òîðà a равен интегралу от дивергенции этого вектора по объему,

ограниченному этой поверхностью. Это утверждение можно рас-

сматривать как определение дивергенции векторного поля, которое

говорит, что дивергенция векторного поля есть объемная плотность

потока этого вектора через замкнутую поверхность.

Математически рассматриваемая теорема записывается как

адмиралаIS (a, dS) = ZV diva dV.

Приступим к рассмотрению теоремы Гаусса. Для этого напом-

ним понятие телесного угла Ω. Если мы возьмем часть поверхности

сферы и ее площадь поделим на квадрат радиуса этой сферы, то

это и будет телесным углом, соответствующим данной поверхно-

сти сферы, т.е. Ω = S/R2. Получаемая величина безразмерна, но

по аналогии с плоским углом, определенным в радианах, телесный

угол определяется в стерадианах.

имени

Ф

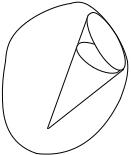
Теперь возьмем произвольный точечный заряд q и окружим его

произвольной поверхностью S (рис. 8). Подсчитаем поток напря-

женности E, создаваемый зарядом и проходящий через S. Поток

dS0 проекция dS на направление, перпендикулярное к радиус-

вектору r, проведенному от заряда q до области поверхности dS.

Подставляя выражение для E, получаем

Мак

dΦ =

1 q

dS0

=

1

q dΩ,

4πε0

r2

4πε0

откуда видно, что элементарный поток зависит лишь от заряда q

и телесного угла dΩ. Здесь важно, чтобы заряд находился внутри

интегрировании по всей поверхности нужно проинтегрировать.ýëå-

поверхности S, в противном случае поток будет равен нулю При

ментарный телесный угол dΩ по всей сфере, а это дает 4π, поэтому

Φ = IS dΦ = 4πε0 IS dΩ =

ε0 .

С

.О

q

q

Åñëè

заряд находится снаружи за-

мкнутой поверхности,адмто потокиралчерез нееаравен нулю

S (E, dS) = 0.

мкнутой поверхности, то элементарный

dS

поток может либо не пересечь поверх-

dS0

ность, либо пересечет ее, но четное чис-

ло раз. Так как принято, что выходя-

dΩ

щий из тела поток принимается со зна-

ком плюс, а входящий со знаком минус

и памятуя, что элементарный телесный

q

угол при этом строго фиксирован и ра-

вен как для входящего элементарного

потока, так и для выходящего, то они

Ðèñ. 8:

друг друга в точности компенсируют.

имени

Таким образом, если заряд снаружи за-

При выводе последних соотношений оказалось,

H

что совершенно

не важно, где находится заряд. К тому же помимо одного заря-

да их может быть произвольное число, либо предельный случай

непрерывного его распределения, тогда

(24)

IS

(E, dS) = ε0

i

qi = ε0

ZV

ρdV.

1

X

1

Ф

ние объемной плотности заряда ρ по объему V , находящемуся внут-

Здесь суммирование производится по зарядам, находящимся внут-

ри рассматриваемой поверхности, либо производится интегрирова-

Если по отношению к левой части уравнения (24) применить

V ρdV /ε0. Это уравнение остается неизменным при

R

теорему Гаусса-Остроградского, то получим уравнение

V divE dV =

R

любом объеме,

Мак

это значит, что должны быть равны и подынтегральные выраже-

íèÿ, ò.å.

divE =

1

ρ.

(25)

ε0

оператор Лапласа (div .ϕ =

ента любой скалярной

функции есть

.О

Учитывая уравнение (12) и тот факт, что дивергенция гради-

ϕ = (∂2/∂x2 + ∂2/∂y2 + ∂2/∂z2)ϕ), получим дифференциальное

уравнение для потенциала

С

ϕ = −

ρ

,

(26)

ε0

Кроме того, оказывается,адмиралачто если некоторая функция удовле-

которое называется уравнением Пуассона.

Во всех частях пространства, не содержащего электрических за-

рядов как свободных, так и связанных ρ = 0 и электрический по-

тенциал ϕ удовлетворяет уравнению

ϕ = 0,

(27)

которое называется уравнением Лапласа. Это уравнение относится

к важнейшим уравнениям математической физики. Класс функ-

ций, удовлетворяющих уравнению Лапласа, называется гармони-

ческими функциями. Одно из свойств таких функций заключается

в том, что среднее значение ϕ(x, y, z) по поверхности любой сферы

имени

равно значению ϕ в центре сферы.

творяет уравнению Лапласа, а также граничным условиям на всех

имеющихся поверхностях, то это решение оказывается единствен-

ным. Данное свойство называется теоремой единственности. Тео-

рема единственности позволяет со всей строгостью утверждать, что

если удалось найти или угадать функцию, удовлетворяющую урав-

нению Лапласа и граничным условиям на имеющихся поверхно-

Ф

стях, эта функция и соответствующее решение задачи будет един-

1ственно.8 Примеры.

применения теорема Гаусса

сятся бесконечная плоскость, бесконечная нить или бесконечный

цилиндр, а также сфера и шар. Рассмотрим их.

1. Бесконечная плоскость с поверхностной плотностью за-

Мак

ðÿäà σ. Такая ситуация возникает, когда расстояние до реальной

плоскости много меньше линейных размеров самой плоскости.

Итак, пусть у нас имеется беско-

1

2

нечная плоскость и на каждый ее квад-

σ

ратный метр приходится заряд σ. Â

E

S

E

.

соответствии с рис. 9 мысленно про-

.О

ткнем эту плоскость цилиндром пло-

щадью сечения S и длиной l, перпен-

С

дикулярно и симметрично этой плос-

кости. К этому цилиндру применим

Ðèñ. 9:

теорему Гаусса. В силу предельной сим-

и плоскости, он равенадмиралσS. Применение теперьатеоремы Гаусса дает

метрии понятно, что вектор напряженности будет в любой точке

перпендикулярен плоскости. Это следует из того, что нет никакого

основания для выделенности любого другого направления. Поэто-

му поток через боковую поверхность цилиндра равен нулю. Оста-

лись левое, помеченное на рис. 9 индексом "1", и правое, поме-

ченное индексом "2", донышки. В силу параллельности E è S1,

костиRлевого

R

Φ1 = S1 (E, dS1) = S1 E dS1. Интегрирование здесь идет по плос-

донышка, все точки которого равноудалены от плоско-

сти на расстоянии l/2. Именно поэтому во всех точках этой плоско-

сти напряженность E должна быть неизменной. Это дает возмож-

êîì "2". Ò.å. Φ2

= ES R

Φ = Φ1 + Φ2

= 2ES

ность написать Φ1 = E S1 dS1 = ES. Аналогично будет с доныш-

имени

и общий поток

. Заряд

же внутри цилиндра располагается в местах пересечения цилиндра

2ES = σS/ε0. Откуда для бесконечной плоскости получаем

E = σ .

(28)

2ε0

Заметим,

что для бесконечной плоскости напряженность не за-

Ф

висит от расстояния до плоскости, поэтому в данном случае невоз-

ìè "1"è "2", u12

= ϕ1 − ϕ2 = σ/(2ε0)(x2 − x1), ãäå xi абсолютное

можно говорить о потенциале относительно бесконечности, но мож-

но говорить о разности потенциалов между произвольными точка-

го конденсатора выполняется условие d S, ãäå d расстояние

Мак

между пластинами, это будет случай, когда можно предполагать,

что пластины бесконечны. Кроме того, используя принцип суперпо-

зиции полей для напряженности, получим, что с левой стороны от

обеих пластин напряженность от одной пластины будет направлена

налево, а от второй направо, в результате будет полная компенса-

E = ε0 .

.

.О(29)

ция. Внутри конденсатора поля будут складываться, и напряжен-

ность в плоском конденсаторе оказывается равной

С

σ

адмирала

0

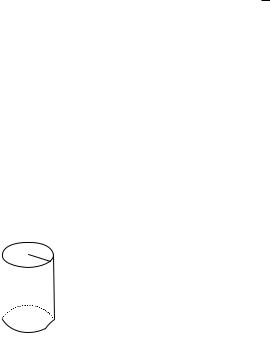
2. Бесконечная нить с линейной плотностью заряда λ, рис. 10.

λ

Ïîä λ понимается заряд, приходящийся

на один метр длины нити. Как и в преды-

R

дущем случае, в силу симметрии напряжен-

L

S

ность поля будет направлена по радиусу от

нити наружу для положительного заряда и

перпендикулярно нити. Нанижем на нить

цилиндр радиусом r и высотой l. Очевид-

но, что в этом случае поток через донышки

равен нулю, а через боковую поверхность

Ðèñ. 10:

Φ = ES = E2πrl, где учтено, что площадь

имени

боковой поверхности цилиндра равна 2πrl.

Заряд же внутри цилиндра равен λl, что приводит к E2πrl = λl/ε ,

откуда получаем для бесконечной нити

λ

E = 2πε0r .

(30)

Â

случае, если нить заменить равномерно заряженным цилин-

Ф

дром с объемной плотностью заряда ρ и радиусом R, то снаружи

предыдущем случае, равен 2πrlE, а заряд внутри него равен πr2lρ.

цилиндра (r > R) результат будет тот же и λ = πR2

ρ. Äëÿ òîãî,