1.5. Математическое ожидание дискретной случайной величины

Пусть дискретная случайная величина принимает значенияс вероятностями, соответственно,. Если при проведениииспытаний значениепоявилось,раз (так что), то среднее арифметическоереализованных значений представляется в виде:

.

Отношение является относительной частотой события. При большом числе испытаний относительные частотыколеблются вокруг соответствующих теоретических вероятностей. Поэтомуколеблется вокруг значения

.

Это является основанием для следующего определения.

Определение. 1. Математическим ожиданием дискретной случайной величины с конечным множеством значенийи с вероятностями этих значений, соответственно,называется число

, (2)

или в краткой записи

.

2. Математическим ожиданием дискретной случайной величины с бесконечным множеством значенийи с вероятностями,называется сумма ряда

. (3)

При этом предполагается, что ряд является абсолютно сходящимся (то есть, существует предел последовательности частичных сумм, составленных из модулей его членов). Если абсолютной сходимости нет, то считают, что математическое ожидание не существует.

Статистический смысл математического ожидания: —это число, вокруг которого колеблется среднее арифметическое реализованных значений случайной величины при большом числе испытаний.

Пример. Пусть дискретная случайная величина имеет закон распределения:

:
:

Тогда .

В соответствии с эмпирическим законом больших чисел, следует ожидать, что при большом числе испытаний среднее арифметическое реализованных значений случайной величины окажется близким к числу .

1.6. Свойства математического ожидания.

1. Если случайная величина является постоянной («неслучайной») величиной:, то есть имеет закон распределения

то , или .

Доказательство. По определению . ▄

2. Постоянный множитель можно выносить за знак математического ожидания: .

Доказательство. Ограничимся случаем конечного множества значений. Пусть закон распределения имеет вид:

.

Рассмотрим два возможных случая.

1) . Тогдаимеет закон распределения

так что , и также.

2) . Тогда условияиравносильны, и поэтому

; .

Следовательно, закон распределения закон распределения случайной величины имеет вид:

.

Поэтому

. ▄

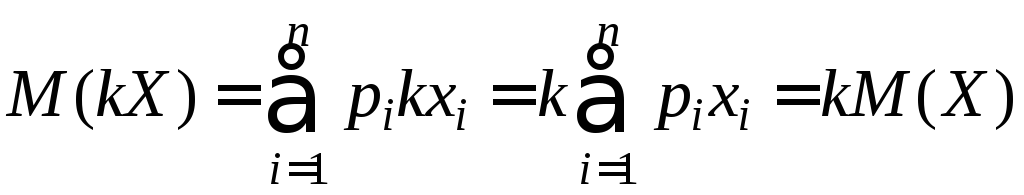3. Теорема сложения для математического ожидания.

Пусть случайные величины и имеют математические ожиданияи. Тогда

.

Доказательство. Ограничимся случаем конечного множества значений. Пусть законы распределения для иимеют вид:

;

.

Случайная величина принимаетзначений вида, где. Ограничимся для простоты случаем, когда все эти значения различны. Пусть—вероятности указанных значений. Тогда

.

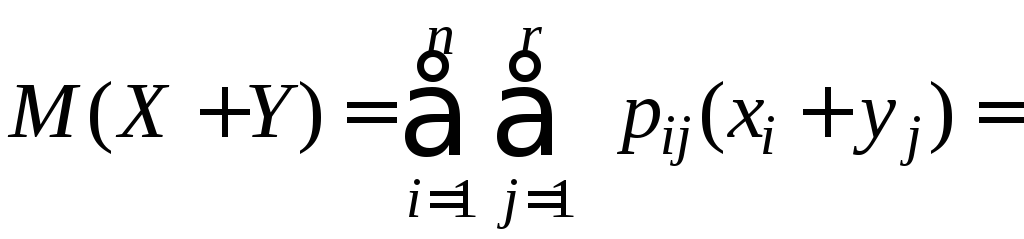
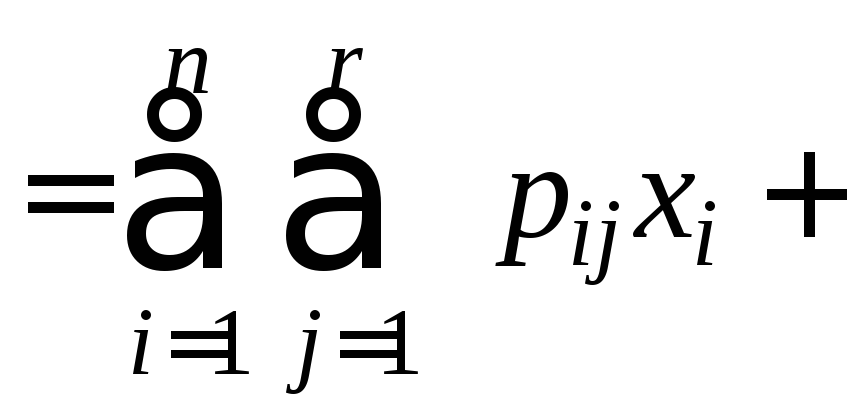
Производя в каждой из двойных сумм группировку слагаемых и вынося за знак внутренней суммы общий множитель (и, соответственно), получаем:

.

Убедимся теперь, что 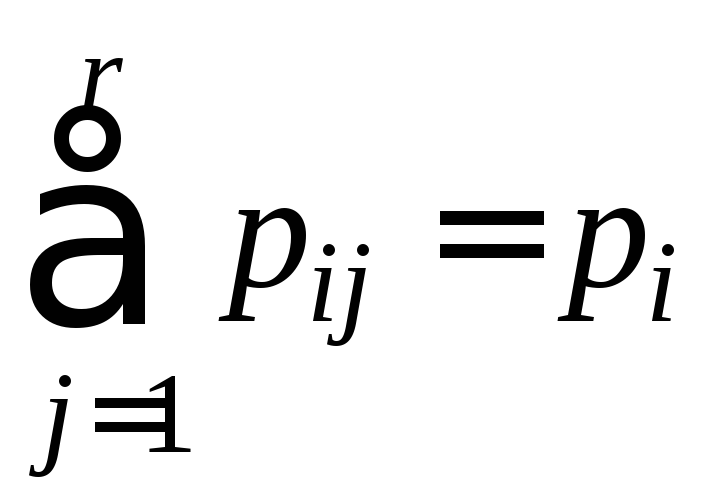. Для этого введем события:;   ;; … ; .

События , а значит, ипопарно несовместны, поэтому (сумма вероятностей событий равна вероятности их суммы):

.

Аналогично 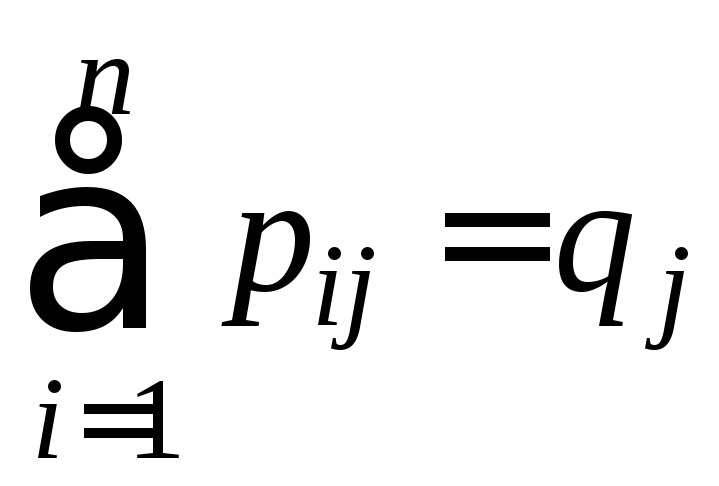. Тогда

. ▄