II. Случай непрерывной двумерной случайной величины.

Пусть непрерывная двумерная случайная величина имеет плотность распределения, а плотности распределения составляющих– функции и– не принимают нулевых значений. Обобщая формулу (40) на непрерывный случай, получаем следующее

Определение. Условной плотностью распределения составляющей при условии называется функция аргумента :

.

Аналогично условной плотностью распределения составляющей при условии называется функция аргумента :

.

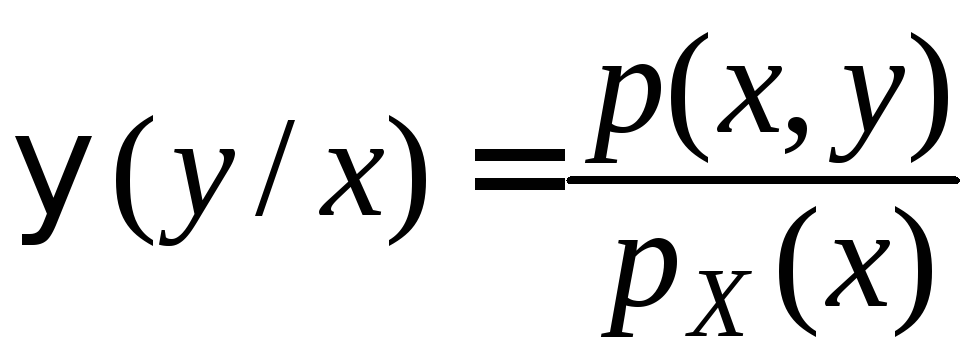4.7. Критерии независимости составляющих

Напомним, что случайные величины и независимы, если для любых промежутковиявляются независимыми событияи, так что вероятность их произведения равна произведению соответствующих вероятностей:

.

Теорема. Для того чтобы составляющие и двумерной случайной величиныбыли независимы, необходимо и достаточно, чтобы ее функция распределениябыла равна произведению функций распределения составляющих:

. (41)

Доказательство. 1. Необходимость. Пусть составляющие и независимы. Тогда

.

2. Не приводя исчерпывающего доказательства, дадим пояснения, относящиеся к достаточности. Пусть . По определению функции распределения в двумерном и одномерном случае, это означает, что

,

то есть события инезависимы. Можно доказать, что тогда и для любых промежутковисобытияитакже независимы. Последнее и означает независимость случайных величини. ▄

Следствие. Для того чтобы составляющие и непрерывной двумерной случайной величиныбыли независимы, необходимо и достаточно, чтобы выполнялось равенство для плотностей:

.

Доказательство. 1. Необходимость. Пусть составляющие и независимы. Тогда справедливо равенство (41). Дифференцируя его дважды пои по, получаем:

, или .

2. Достаточность. Пусть . Интегрируя это равенство по множеству

(см. рис. 14), получаем:

(выносим за знак внутреннего интеграла множители, не зависящие от )

.

Применяя к левой части формулу (35), а к правой — определение функции распределения в одномерном случае (п. 2.1), получаем: . ▄

Список литературы

1. Вентцель Е.С. Теория вероятностей: учебник для вузов. М.: Высшая школа, 2001. — 575 с..

2. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 2002. — 478 с.

3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа, 1979. — 400 с.

4. Гнеденко Б.В., Хинчин А.Я. Элементарное введение в теорию вероятностей. М.: УРСС, 2003. — 205 с.

5. Гнеденко Б.В. Курс теории вероятностей. М.: УРСС, 2001. — 318 с.

6. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Часть II. М.: Высшая школа, 1997. — 416 с.

7. Коваленко И.Н., Филиппова А.А. Теория вероятностей и математическая статистика. М.: Высшая школа, 1982. — 256 с.

8. Шкадова А.Р., Нырков А.П. Теория вероятностей. СПб.: СПГУВК, 2003. — 198 с.

9. Ястребов М.Ю. Схема равновозможных исходов. СПб.: СПГУВК. 1994. — 13 с.

10. Ястребов М.Ю. Производная и исследование функций. СПб.: СПГУВК. 2003. — 45 с.

11. Ястребов М.Ю. Введение в математическую логику. СПб.: СПГУВК, 2003. — 71 с.

12. Ястребов М.Ю. Математика. Неопределенный и определенный интегралы. СПб.: СПГУВК. 2004. — 55 с.

13. Ястребов М.Ю. Математика. Теория вероятностей. Часть I. Вероятности случайных событий. СПб.: СПГУВК, 2004. — 43 с.