
ГЛАВА-1-06.13
.pdf
8.10. y(x) log2 (3cos |
|
arctg4 |
5x2 |
), |
dy ? |
||
x |
|||||||
|
|
||||||
|
|
|
|
8 |
|
|
|
8.11. xy cos(x y) 0, |
dy ? |
|
|||||
8.12. x y sin(x y) 0, |
dy ? |
|
|||||
|
|
1 |
|
|
|
|
|
|||||||
8.13. |
dy ex |
|
|
|
|
|
|
|
|
dx, |
y ? |
|||
|
|
|
|
|
|
|
|
|||||||
1 x2 |
||||||||||||||
|
|
|
|
|||||||||||
|
|
|
||||||||||||
|
1 |
|
|
|
1 |
|
|
|
|
|
||||
8.14. |
dy |
|
|
|
|
|
|
|
dx, |
y ? |
||||
|
|
x |
2 |
|||||||||||
|
x ln 3 |
1 |
|
|
|
|
|
|||||||
|
dy 3arcsin2 ln x |
|
|
1 |
|
|
|
|
|
1 |
dx, |
|
y ? |
|
|||||||||
8.15. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
ln2 x |
x |
|
|
|||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
arctg5 |
1 |
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
dy 2 |
|
x ln 2 5arctg4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx, |
y ? |
||||
|
|
|
|
|
|
|
1 |
|
|
|
2 |
||||||||||||
8.16. |
|
|
|
|
|
|
|
x |
1 |
|
|
|
|
x |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответы
8.1.1) при ∆x = 0,1; ∆y = 0,11; dy = 0,1; 2) при ∆x = 0,01; ∆y = 0,0101; dy = 0,01;
8.2.1) при ∆x = 0,1; ∆y = 2,411; dy = 2,5; 2) при ∆x = 0,01; ∆y = 0,249101, dy = 0,25.; 8.4. 28,66 м2; 8.5. 0,513; 8.6. 0,775; 8.7. 1,007; 8.8. 1,999;
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
8.9. dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
x |
2 |
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
x2 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
8.10. |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
3cos |
x ln 3 sin |
x |
|
1 |
|
|
4 arctg3 |
5x |
|
|
|
|
1 |
|
|
5x |
|
dx ; |
|||
|
|
|
|
|
|
4 5x2 |
|
|
|
|
|
|
|
|
|
|
|
|
25x4 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
arctg |
|
ln 2 |
|
|
|
|
2 |
|
x |
8 |
|
|
|
|
|
|
4 |
|
|
||||||||||||||||
|
cos x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
64 |
|
|
|
|
|
|||||
8.11. |
sin(x y) y |
dx ; 8.12. |
1 cos(x y) |
dx ; 8.13. y1 ex arcsin x c, |
|||||||
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||
|
|
|
sin(x y) y |
1 cos(x y) |
|||||||
y |
ex arccos x c, где c const ; 8.14. y1 log3 x arctg x c, |
||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
y |
2 |
log |
3 |
x arcctg x c, где с const ; 8.15. y arcsin3 ln x с ; |
|||||||
|
|
|
|
|
|
|
|
|
|
||
8.16. y 2arctg |
5 1 |
|
|
|
|
||||||
|
x |
c . |
|
|
|||||||
41
§9. Производные и дифференциалы высших порядков
Производная f (x) от функции f (x) называется производной первого порядка или первой производной и представляет собой некоторую функцию, которая также может иметь производную. Тогда производная от производной первого порядка называется производной второго порядка или второй производной. Ее обозначают одним из следующих символов:
|
|
d2 y |
|
d dy |
|||
|
, |
|
|
|
. |
||
f (x), y , |
dx2 |
|
|
||||
|
|
|
dx dx |
||||
Производная от производной |
второго |
порядка, если она существует, |
|||||
называется производной третьего порядка или третьей производной. Аналогично определяются производные четвертого, пятого и т.д. порядков.
Вообще, производной n-го порядка от функции |
y f (x) называется |
|||||||||||||||||||||||||
производная от производной (n–1)-го порядка: |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f n ( x) f (n 1) x |
|
|
|
|||||||||||||||||||||||
Производные высших порядков вычисляются последовательным |
||||||||||||||||||||||||||
дифференцированием функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если функция y x задана параметрически системой уравнений: x t , |
||||||||||||||||||||||||||
где t и ψ t − дифференцируемые функции и |
|
|
y ψ t |
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
t 0 , то для нахождения |
|||||||||||||||||||||||||
производных функции y x можно использовать следующие формулы: |
||||||||||||||||||||||||||
|
|
|
dy |
|
|
|
ψ t |
|
|
|
yt |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
yx |
|
dx |
|
|
t |
|
|
xt |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
d |
2 |
y |
|
|
|
|
|
|
|
|
|||||
|
y |
|
|
|
|
|
|
|
y t |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
и т.д. |
||||||||||||
2 |
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||
yxx |
x |
|
dx |
|
|
|
xt |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d y |
|
|
|
|
|
t |
|
|||||||
|
|
y |
|
|
|
|
|
|
yxx |
|
||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|||||||||||||
yxxx |
|
x |
3 |
|
|
dx |
|
|
xt |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Производную второго порядка можно также вычислить по формуле:
|
|
|
|
|
|
|
|
|
ytt |
xt |
xtt |
yt |
|
|
|
|
|
|
|
|
|
yxx |
|
xt 3 |
|
|
|
|
|
|
|
|
||
Для нахождения второй производной от функции, заданной неявно, |
||||||
равенство y |
f x, y , задающее ее первую производную, дифференцируют по |
|||||
x (рассматривая y как функцию от x ), |
а затем в правой части полученного |
равенства на место y подставляют |
задающее ее выражение f x, y . |
Аналогично поступают при нахождении производных более высоких порядков.
42

Дифференциалом второго порядка функции y f ( x) называется дифференциал от дифференциала первого порядка этой функции:
d2 y d dy
Аналогично определяется дифференциал третьего порядка: d3 y d d2 y
Вообще, dn y d dn 1 y .
Если y f ( x) и x – независимая переменная, то дифференциалы высших порядков вычисляются по формулам:
d2 y y dx2 d3 y y dx3
_________
dn y y n dxn
Свойством инвариантости дифференциалы высших порядков (начиная со второго) не обладают.
Примеры с решениями Пример 1. Найти y от функции y cos2 3x
Решение.
y (cos2 3x) 2 cos3x ( sin 3x) 3 3sin 6x y ( y ) ( 3sin 6x) 3cos 6x 6 18cos 6x
y ( y ) ( 18cos 6x) 18( sin 6x) 6 108sin 6x Ответ: y 108sin 6x
Пример 2. Найти производную n-го порядка от функции y sin x Решение. Определяем последовательно y , y , y , y(4) :
y cos x, y sin x, y cos x, y(4) sin x y
Мы установили закон, по которому строятся последовательные производные от y sin x . Теперь можно дать и общую формулу для n-й
производной от этой функции. Действительно,
y cos x sin x
π
2
43

π
2
π
2
|
|
|
|
y |
4 |
sin x sin x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
sin x 4 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
|
|
|
______________________________ |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
(n) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
nπ |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
sin |
x |
|
n |
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
(n) |
|
|
|
|
|
|
|
|
nπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Ответ: y |
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функции y x , |
||||||
Пример 3. |
Найти |
|
|
производную |
третьего |
порядка |
от |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 4 cos t |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
заданной параметрически уравнениями |
|
|
|
|
5 sin t |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yt |
|
|
|
|
|
|
5 cos t |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ctgt |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
yx |
xt |
|
|
4 sin t |
|
4 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
4 |
|
|
|
sin |
|
t |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
yx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
yx 2 |
|
|
|
|
|
xt |
|
|
4 |
sin t |
|
|
|
|
|
|
|
|
|
3 |
t |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 sin |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
y 2 |
t |
|
|
|
|
|
|
|
|
|
|
|
3 sin |
|
|
|
|
t |
cos t |
|
|
|
|
15 cos t |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
yx 3 |
|
xt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 sin t |
|
|
|
|
|
|
|
|
|
|
|
64 sin |
5 |
t |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
15 cost |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ответ: yx3 |
64sin |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y x , если она |
||||||||||
Пример 4. Найти производную n-го порядка от функции |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ln t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
задана параметрически уравнениями |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yx |
|
|
xt |
1 |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
t
44

yx 3
Ответ: dn y 1 n 1 dxn t
|
|
|
|
y |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
y 2 |
|
|
t |
|
|
|
|
|
|
t |
2 |
|
|
|
|
|
|
||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 |
|
|
|
|
t |
|
|||||||||||||||||
|
x |
|
|
|
xt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
y 2 t |
|
|
|
t |
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и т.д. |
|||||||||
|
xt |
|
|
|
1 |
|
|
|
t |
|
|||||||||||||||||
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
1 |
|
|
|
|
|
|
|
||||||
|
|
y |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
t |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 5. Найти производную второго порядка от |
функции y( x) , |
|
|
|||||||||||||||||||||||||
заданной неявно уравнением y3 2xy 3 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Решение. |
Найдем y , продифференцировав по |
|
x обе части уравнения, |
|
|
|||||||||||||||||||||||
задающего неявно функцию y( x) , рассматривая при этом y как функцию от x . |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3y y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
2 y xy 0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
3y2 y 2 y 2xy 0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
2x 2 y |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
y 3y |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
y |
|
|
2 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
3y 2 2x |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Теперь |
продифференцируем |
|
по |
|
|
x обе |
|
части |
|
полученного равенства |
|
|
||||||||||||||||
(рассматривая y как функцию от x ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
3y |
2 |
2x y 6 y y |
|
2 |
|
|
|
|
|
|
|
2 |
2x 6 y |
2 |
|
2 y |
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
y 2 |
y |
|
|
2 |
y 3y |
|
|
|
|
2 |
2 y y 2x 3y |
|
||||||||||||||||
|
|
|
3y 2 2x 2 |
|
|
|
3y 2 2x 2 |
|
|
3y 2 2x 2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
И теперь в полученное выражение подставим |
|
y |
|
|
|
2 y |
: |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
3y |
2 |
2x |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
45

|
2 y |
2 y |
|
|
|
2x 3y 2 |
|
|
2x 2x 3y 2 |
|
|
|
|
|
|||
|
|
|
|
|
3y 2 |
|
|
|
|
||||||||
3y 2 |
|
|
|
|
|
16xy |
|||||||||||
y 2 |
|
2x |
|
|
4 y |
|
|||||||||||
|
3y 2 2x 2 |
|
|
3y 2 2x 3 |
|
|
3y 2 2x 3 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
Ответ: y |
|
|
|
16xy |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3y 2 2x 3 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 6. Найти дифференциал 22-го порядка функции y 2x |
|||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
d22 y y 22 dx22 |
|
|
|
|
|
|
||
y 2x ln 2, y ln 2 2x ln 2 2x ln 2 2, y ln 2 2 2x ln 2 |
2x ln 3 2,..., y n |
||||||||||||||||
2x ln n 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, |
y(22) 2x ln22 |
2,тогда d22 y 2x ln 22 2 dx22 |
|
|
|
||||||||||||
Ответ: d22 y 2x ln 22 2 dx22
Примеры для самостоятельного решения
9.1.Найти производные второго и третьего порядков от функции y cos2 4x .
9.2.Найти производные второго и третьего порядков от функции y sin 2 5x .
9.3.Найти производные второго порядка от функции y 
 5x2 3 .
5x2 3 .
9.4.Найти производные второго порядка от функции y 
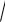 7x2 4 .
7x2 4 .
9.5.Найти производную третьего порядка от функции y arctg3x .
9.6.Найти производную третьего порядка от функции y arcctg2x .
9.7. Найти d2 y , если dx 2
9.8. Найти d2 y , если dx 2
|
|
|
3 |
|
|
|
x a cos |
t |
|
|
|||
|
. |
|
||||
|
|
3 |
|
|
||
|
|
|
|
|
||
y a sin |
t |
|
|
|||
|
|
|
|
|||
x a t sin t |
|
|||||
|
cost) |
. |
||||
y a(1 |
|
|||||
46

9.9. Найти y , если
xx
9.10. Найти y , если
xx
9.11.Найти y x2 , если
9.12.Найти yx 2 , если
|
|
|
|
|
|
|
|
|
t |
||
x arccos |
|||||
|
|
|
|
. |
|
|
2 |
|
|||
|
|
|
|
|
|
y |
t t |
|
|
|
|
x et
.
y arcsin t
|
t |
|
|
|
x e |
cost |
|
|
|
|
. |
|
||
|
t |
|
|
|
|
|
|
|
|
y e |
sin t |
|
|
|
|
|
|
||
x a sin t t cost |
|
|||
|
|
|
|
. |
y a cost t sin t |
|
|||
9.13.Найти производную второго порядка от функции y( x) , заданной неявно уравнением: arctgy y x 0 .
9.14.Найти производную второго порядка от функции y( x) , заданной неявно уравнением: xy3 2 y 1 0.
9.15.Найти значение производной второго порядка от функции y( x) в точке (1;1) , если функция задана неявно уравнением x3 2xy 3y2 0.
9.16.Найти значение производной второго порядка от функции y( x) в точке (1;1) , если функция задана неявно уравнением y3 2 y2 xy x3 3x2 0 .
9.17. Найти производную n-го порядка от функции |
y |
1 |
|
. |
|
|
|||
3x 2 |
||||
9.18. Найти производную n-го порядка от функции |
y |
1 |
. |
|
|
||||
5x 8 |
||||
9.19.Найти производную n-го порядка от функции y 2x 2 x .
9.20.Найти производную n-го порядка от функции y 3 x 3x .
9.21. Показать, что функция |
y sin ln x cos ln x удовлетворяет уравнению |
|||
x2 y x y y 0. |
|
|
|
|
9.22. |
Показать, |
что |
функция |
y ex 3cos2x 2sin 2x e2x x 1 |
удовлетворяет уравнению y 2 y 5y e2x 5x 7 .
47

9.23.Найти дифференциалы второго, третьего, четвертого и n-го порядков функции y 2x 3 3 .
9.24.Найти дифференциалы второго, третьего, четвертого и n-го порядков функции y e2x .
9.25. |
Найти |
|
дифференциалы |
|
второго |
и |
|
третьего |
|
порядков функции |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
y x ln x 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
9.26. Найти дифференциал второго порядка функции y ln x |
|
|
|
|
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x2 2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
9.1. |
y 32cos8x, y 256sin 8x ; |
|
|
|
|
|
9.2. |
|
|
y 50cos10x, y 500sin 10x ; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
9.3. y |
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
; 9.4. y |
|
|
|
|
|
|
|
|
28 |
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
5x 2 3 |
|
|
|
|
|
|
|
|
|
|
7x2 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
5x 2 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7x 2 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
54 27x |
2 |
1 |
|
|
|
|
|
|
16 1 |
12x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
9.5. y |
|
|
|
; 9.6. |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
9x |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 4x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
9.7. y |
16 1 12x2 d2 y |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d2 y |
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; 9.8. |
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3a sin t cos4 t |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
4x2 |
1 3 |
|
|
|
dx2 |
|
|
dx2 |
4a sin |
4 t |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t 2 t 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
4 |
|
|
t |
t |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
9.9. yxx |
|
|
|
|
; 9.10. |
yxx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2t 1 t 2 |
1 t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
9.11. |
y |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
; 9.12. |
y |
|
|
|
|
|
|
|
1 |
|
|
|
|
; 9.13. |
|
y |
|
2 |
1 y2 |
; |
||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
x |
|
|
|
e |
t |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
at sin |
3 |
t |
|
|
|
|
|
|
|
|
|
y |
5 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
cost sin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
12 y5 |
xy2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
3xy2 |
2 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
9.14. |
y |
|
|
|
|
|
|
; 9.15. y |
|
1;1 |
|
|
32 ; 9.16. y 1;1 27 ; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
9.17. y(n) |
|
|
|
3 n n! |
|
|
|
; 9.18. |
|
y(n) |
|
|
|
|
5 n n! |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
3x 2 n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5x 8 n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
9.19.y(n) 2x 1 n 2 x ln n 2 ;
9.20.y(n) 1 n 3 x 3x ln n 3; 9.23. d2 y 24 2x 3 dx2; d3 y 48dx3;
48

d4 y 0,dn y 0; 9.24. d2 y 4 e2x |
dx2; d3 y 8 e2x dx3; d4 y 16 e2 x dx4; |
|
||||||||
dn y 2n e2x dxn ; 9.25. d2 y |
dx2 |
|
;d3 y |
dx3 |
; 9.26. |
d2 y |
x |
|
|
dx2 . |
x |
|
x2 |
x2 2 |
|
|
|||||
|
x2 2 |
|||||||||
§10. Раскрытие неопределѐнностей. Правило Лопиталя
При решении задач, связанных с вычислением пределов функций, часто непосредственная подстановка предельного значения аргумента приводит к
неопределѐнным выражениям вида: |
|
0 |
, |
|
, 0 , , 00 |
, 0 , 1 . |
|
|
|
||||
|
0 |
|
|
|
||
|
|
|
|
|
|
Нахождение предела в таких случаях называют раскрытием соответствующей неопределенности. Довольно часто справиться с этой проблемой помогает так
называемое правило Лопиталя, которое можно сформулировать в виде теоремы. |
|||||||||||||||||||||||
|
Теорема. Если |
функции |
|
f x |
и |
g x |
|
|
удовлетворяют |
следующим |
|||||||||||||
условиям: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1) |
lim f x lim |
g x 0 или |
lim f x lim |
g x ; |
|
|
|
||||||||||||||||
|
x x0 |
x x0 |
|
|
|
|
x x0 |
x x0 |
|
|
|
|
|
|
|
||||||||
2) |
f x |
и g x |
дифференцируемы |
в некоторой окрестности |
точки |
x0 , |
и |
||||||||||||||||
|
для любого |
x их этой окрестности (за исключением, |
может быть, |
||||||||||||||||||||
g |
x 0 |
||||||||||||||||||||||
самой точки x0 ); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|||
3) существует (конечный или бесконечный) |
lim |
x |
, то тогда |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
f x |
|
x x0 |
g x |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
lim |
|
lim |
|
f x |
. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
x x0 g x |
x x0 g x |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание 1. Если lim |
|
f x |
не существует, |
то нельзя ничего сказать об |
||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
x x0 |
|
g x |
|
|
|
|
|
|
|
|
|
|
|
||||||
исходном |
пределе, |
т.е. lim |
f x |
может |
существовать, а |
может |
и |
не |
|||||||||||||||
g x |
|
||||||||||||||||||||||
|
|
|
|
x x0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
существовать. В такой ситуации решать задачу вычисления предела надо без использования правила Лопиталя.
Замечание 2. Правилом Лопиталя можно пользоваться (в случае
выполнения условий теоремы) при раскрытии неопределенностей вида 0 или
0
|
|
не |
только |
при |
x x0 , |
но |
и |
при |
|
|
|||||||
|
|
|
|
|
|
|
|
|
x x0 0, x x0 0, x , x , x .
49

Замечание 3. Правило Лопиталя в некоторых задачах можно применять повторно.
Если необходимо раскрыть неопределенности иного вида, нежели 0 и0
,
то следует преобразовывать функцию, стоящую под знаком предела, приведя еѐ к виду, позволяющему применить правило Лопиталя.
|
Если при |
|
x x0 |
x 0 , а |
ψ x , то вычисление предела |
||||
lim |
x ψ x (неопределенность вида 0 ) может быть сведено к одному |
||||||||
x x0 |
|
|
|
|
|
|
|
|
|
из |
случаев |
0 |
|
или |
|
|
при помощи тождественных преобразований |
||
|
|
|
|
|
|||||
|
|||||||||
|
|
0 |
|
|
|
|
|
|
|
произведения в частное:
x ψ x |
x |
|
или x ψ x |
|
ψ x |
|
|
|
||||||||
1 ψ x |
1 x |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Если |
при |
x x0 |
x , |
а |
|
ψ x , то вычисление предела |
||||||||||
lim x ψ x (неопределенность |
вида |
) может |
быть сведено к |
|||||||||||||
x x0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||
раскрытию |
неопределенности |
путем |
тождественного |
преобразования |
||||||||||||
разности в произведение: |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
||
x |
ψ x x |
ψ x |
|
|
|
|
|
|
|
. |
|
|
||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
ψ x |
|
|
x |
|
|
||||||
Иногда удобно пользоваться и другими преобразованиями:
|
|
ψ x |
x |
|
||
x ψ x x 1 |
|
|
|
или x ψ x ψ x |
ψ x |
1 |
|
||||||
|
|
x |
|
|
||
При |
вычислении |
пределов |
x |
можно столкнуться с |
|||
вида lim x |
|||||||
|
|
|
|
|
|
x x0 |
|
неопределенностью 00 или 0 , или 10 . Раскрытие этих неопределенностей |
|||||||
производят с помощью следующего преобразования: |
|
||||||
|
x |
|
|
x |
|
x ln x |
|
|
e |
ln x |
|
||||
x |
|
|
e |
|
|
||
|
|
|
|
|
|
|
|
50
