
ГЛАВА-1-06.13
.pdf
Из соотношения ch2 y sh2 y 1 выразим ch2 y 1 sh2 y , а поскольку ch y 0
для всех y R , то получим ch y 
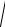 1 sh2 y , где sh y x .
1 sh2 y , где sh y x .
|
y 'x |
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
Таким образом, |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
ch y |
|
sh2 y |
|
x2 . |
|||||||||
|
|
1 |
1 |
||||||||||
Итак, формула производной функции, обратной к гиперболическому синусу, имеет вид:
|
|
|
|
|
(arsh x) ' |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||
Ответ: (arsh x) ' |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Примеры для самостоятельного решения |
|
|
|||||||||||||||||||||
Найти производную |
|
|
от функции y = y(x), заданной неявно уравнением: |
|||||||||||||||||||||
yx |
||||||||||||||||||||||||
6.1. x3 y3 |
3xy 0 |
|
|
|
|
|
6.5. x y yx |
|
|
|||||||||||||||
6.2. x6 y6 |
3x2 y2 |
6x 12y 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
y |
ey |
x 3 |
y |
|
|
0 |
||||||||||||||||
|
|
|
|
|
|
6.6. |
|
|
|
|
|
|||||||||||||
6.3. x3 ln y x2ey |
0 |
|
|
|
|
x |
|
|
|
|
x |
|
|
|||||||||||
6.4. xsin y y sin x 0 |
|
|
|
6.7. |
arctg |
y |
|
1 |
ln(x2 |
y2 ) |
||||||||||||||
|
|
|
x |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
6.8. Доказать, что функция y(x), заданная неявно уравнением xy ln y 1,
удовлетворяет также уравнению y2 (xy 1) y ' 0 . Продифференцировать функции, используя логарифмическую
производную:
|
|
arctg |
1 |
|
|
|
|
|
(x2 4)3 |
(x 2)3 |
|
|
|
||||
6.9. y (sin 3x) |
x |
6.13. y |
4 |
|
|
|
|||||||||||
|
|
|
|
(x 1)(x |
2 |
x 2) |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
6.10. |
y (cos 2x)tg5 x |
|
|
|
|
|
|
|
|
|
5 |
|
|
6 |
|||
|
|
|
|
|
x 3 (x 1) |
x |
|||||||||||
|
|
|
|
|
6.14. y |
|
|
|
|
|
|
||||||
|
y (x2 2)sh x |
|
|
||||||||||||||
6.11. |
|
(2 x)4 (x 5)2 (2x 1)3 |
|||||||||||||||
6.12. |
y (cth x)ch x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6.15. Составить уравнения касательной и нормали к графику функции y = y(x)
в точке M0 (1;1) , если функция задана уравнением x3 2x2 y2 5x y 5 0.
31

6.16. Составить уравнения касательной и нормали к графику функции y=y(x) в точке M0=(–2; 1), если функция задана уравнением
2x2 3xy3 5x 3y 1 0
Найти производные функций, обратных к заданным:
6.17. |
y ch x, x (0; ) |
6.20. |
y arccos 2x |
|
|
|
6.18. |
y cos x |
|
y 2x2 x, x ( |
1 |
|
; ) |
|
|
6.21. |
|
|||
6.19. |
y arcsin 3x |
2 |
|
|||
|
|
|
|
|||
6.22. Составить уравнения касательных к графику функции y x3 |
и к графику |
|||||
обратной к ней функции, проходящих через точку Mo(1; 1). Сделать чертѐж.
6.23. Составить уравнения касательных к графику функции |
y |
1 |
x2 |
и к |
||||||||||||||||||||||
2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
графику обратной к ней функции, проходящих через точку M0(2; 2). Сделать |
||||||||||||||||||||||||||
чертѐж. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответы |
|
|
|
|
|
|
|
|
|
|
||
6.1. y ' |
x |
2 |
y |
|
xy |
2 |
x |
5 |
1 |
|
|
(2xe |
y |
3x |
2 |
) y |
|
|
|
|
||||||
|
y ' |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
; 6.2. |
|
|
|
|
|
|
|
|
; 6.3. |
y ' |
|
|
; |
|
|
|
||||||
|
y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
x |
y |
5 |
x |
2 |
y 2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
1 x2 yey |
|
|
|
|||||||||||||||
6.4. y ' sin y y cos x ; 6.5. sin x x cos y
y ' |
y(x ln y y) |
; 6.6. |
y ' |
y |
; 6.7. |
y ' |
x y |
; |
|
x( y ln x x) |
x |
x y |
|||||||
|
|
|
|
|
|
|
|
arcctg |
1 |
ln sin 3x |
|
1 |
|
|
|
|
|
|
|||||
6.9. |
y ' (sin 3x) |
|
x |
|
|
3ctg 3x arcctg |
|
|
|
x2 1 |
|
||||||
|
|
|
|
|
x |
|
||
|
|
|
5 ln cos 2x |
|
|
|
|
6.10. |
y ' (cos 2x)tg 5 x |
|
2 tg 2x tg 5x |
||||
cos2 5x |
|||||||
|
|
|
|
|
|||
|
|
|
|
|
2x sh x |
||
6.11. |
y ' (x2 |
2)sh x ch x ln(x2 2) |
|
|
|||
x2 2 |
|||||||
|
|
|
|
|
|||
|
ch x |
|
1 |
|
6.12. y ' (cth x) |
|
sh x ln cht x |
|
|
|
|
|||
|
|
|
sh x |
|
6.13. |
y ' |
1 |
|
|
|
|
(x4 4)3 (x 2)5 |
|
|
|
6x |
|
|
|
5 |
|
|
|
|
1 |
|
|
|
|
2x 1 |
|
|
|
|
|||||||||||||||
|
4 |
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||
|
|
4 |
|
|
(x 1)(x |
|
|
x 2) |
|
x |
|
4 |
|
|
|
x 2 |
|
x 1 |
|
x |
|
x 2 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
x 3 (x 1)5 x6 |
|
|
|
1 |
|
|
|
|
5 |
|
|
|
6 |
|
|
|
4 |
|
|
|
2 |
|
|
6 |
|
||||||||||||
6.14. |
y ' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(2 x) |
4 |
(x 5) |
2 |
(2x 1) |
3 |
2(x 3) |
x 1 |
|
|
x |
|
x 5 |
2x 1 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
|||||||||||||||||||||||||||||||
32

6.15. |
4x 3y 1 0, |
|
|
3x 4 y 7 0 ; 6.16. |
2x 5y 9 0, |
|
5x 2 y 8 0 ; |
|||||||||||||||
6.17. |
(arch x) ' |
|
1 |
|
|
, x (1; ) ; 6.18. (arccos x) ' |
|
|
1 |
|
, x ( 1;1) ; |
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
x2 1 |
|
|
||||||||||||||||||||
|
|
x2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||
6.19. |
|
ctg x |
log3 e ctg x ; 6.20. |
tg x |
log |
2 e tg x ; 6.21. |
1 |
|
||||||||||||||
|
|
|
|
|||||||||||||||||||
|
ln 3 |
ln 2 |
|
|
|
|||||||||||||||||
|
|
|
|
|||||||||||||||||||
|
8x 1 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
6.22. |
|
y 3x 2, |
y |
1 |
x |
2 |
; 6.23. |
y 2x 2, |
y |
1 |
x 1 . |
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
3 |
3 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
§7. Дифференцирование функций, заданных параметрически
Зависимость между переменными x и y иногда удобно задавать двумя уравнениями
x (t) |
|
|
|
(1) |
|
y (t), |
||
|
где t – вспомогательная переменная (параметр). Такое задание функции y(x) называют параметрическим заданием. Особенно часто его используют в механике, где параметр t обычно обозначает время, а уравнения системы (1) представляют собой параметрические уравнения траектории движущейся точки M (x; y).
Исключив из уравнений (1) переменный параметр t , если это возможно, получают явное или неявное задание функции y=y(x).
Полезно знать параметрические уравнения следующих кривых:
x a cos t
1)окружности: y a sin t
x a cos t
2)эллипса: y bsin t
3)циклоиды:
4)астроиды:
x a (t sin t)y a (1 cos t)
x 4 cos3 t
y 4 sin3 t
33
Если функция y=y(x) задана параметрически системой уравнений
x (t) |
где функции (t) и |
(t) дифференцируемы и |
'(t) 0 , то производная |
||||
|
|||||||
y (t) |
|
|
|
|
|
|
|
этой функции может быть вычислена по формуле |
|
||||||
|
|
y 'x |
'(t) |
|
y 't |
. |
(2) |
|
|
'(t) |
|
||||
|
|
|
|
x ' |
|
||
|
|
|
|
|
t |
|
|
Примеры с решениями Пример 1. Определить вид кривой, заданной параметрически системой
уравнений:
x t 2
y 2t2 1 1.
Решение. Из первого уравнения системы выразим переменную t через x и подставим во второе уравнение t x 2 , получим функцию y, зависящую от x:
y 2 (x 2)2 (x 2) 1, y 2x2 8x 8 x 2 1
y 2x2 9x 11. Графиком полученной функции является парабола. Ответ: парабола y 2x2 9x 11.
Пример 2. Определить вид кривой, заданной параметрически системой
x 2 cos t
уравнений y 2sin t.
Решение. Возведѐм в квадрат обе части каждого уравнения системы, а затем сложим левые и правые части полученных уравнений.
x2 4 cos2 t
y2 4 sin 2 t
x2 y2 4 cos2 t 4 sin2 t x2 y2 4(cos2 t sin2 t)
x2 y2 4
Ответ: x2 y2 4 – уравнение окружности с центром в начале координат и радиусом R = 2.
34

Пример 3. Найти производную функции y = y(x), заданной параметрически
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x t |
|
|
|
|
|
|
|
|
|
|||
|
|
5 |
|
|
|
|
|
|
|
|
|
||
уравнениями |
|
|
|
|
|
|
|
|
|
|
|
|
|
y t7 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 't |
|
7t |
6 |
|
7 |
|
Решение. Воспользуемся формулой (2) |
y 'x |
|
|
|
|
t2 |
|||||||
x ' |
5t |
4 |
5 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
Ответ: |
y 'x |
|
7 |
t2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
Примеры для самостоятельного решения
Определить вид кривой, заданной параметрически системой уравнений, и нарисовать еѐ.
x 5t 3
7.1.y 4 3t
x t 4
7.2.y 7t 3
x 3cos t
7.3.y 5sin t
x 4cos t
7.4.y 4sin t
x 3t2 t 2
7.5.y 1 t
x 2t 4
7.6.y 3 t2
Найти производную функции y = y(x), заданной параметрически системой уравнений
|
|
|
|
|
|
|
x a ch t |
|||||
|
x a cos |
3 |
t |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
7.11. |
|
|
|
|
||
7.7. |
y a sin3 t |
|
y b sh t |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x a cos t |
|
|
|
2t t2 |
|||||||
|
|
|
x |
|
|
|
|
|||||
7.8. |
|
|
1 t |
3 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
|
y b sin t |
|
7.12. |
|
2t t |
2 |
|
|||||
|
|
|
|
|
|
|
|
y |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2t |
|
|
|
1 t |
|
|
||||
|
x 3 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
7.9. |
|
t 1 |
|
|
|
|
|
|
||||
|
y 5t 2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x 4 t3
y 3 2t 1
35
|
|
|
x t sin t |
|
|||||
7.13. Составить уравнения касательной и нормали к циклоиде |
|
|
|
|
, |
||||
|
|
|
y 1 |
cos t |
|
||||
проведенных в точке, для которой t = |
. |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
x |
|
2 cos |
|
t |
|
||
7.14. Составить уравнения касательной и нормали к астроиде |
y |
|
|
sin3 t , |
|
||||
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
проведенных в точке, для которой t = |
. |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
x 5cos t |
|
|
|
|
|||
7.15. Составить уравнения касательной и нормали к эллипсу |
|
7sin t |
, |
|
|
||||
|
|
y |
|
|
|
|
|||
проведенных в точке, для которой t = |
. Сделать чертѐж. |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
x 2cos t |
|
|
|
|
|||
7.16. Составить уравнения касательной и нормали к эллипсу |
|
|
|
|
, |
|
|
||
|
|
y |
4sin t |
|
|
|
|
||
проведенных в точке, для которой t = |
. Сделать чертѐж. |
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
7.17. Составить уравнения касательной и нормали к |
кривой, заданной |
||||||||
|
|
|
|
|
|
x t |
2 |
2 |
|
параметрически системой уравнений |
|
, |
||
|
y 2t 3 |
|
||
проведенных в точке М0 (–1;1) |
|
|
|
|
7.18. Составить уравнения касательной и |
нормали к кривой, заданной |
|||
x 3t 2
параметрически системой уравнений ,
y 1 t 2t2
проведенных в точке М0 (1;–2)
Ответы
7.1. 3x + 5y – 11= 0 – уравнение прямой; 7.2. y = 7x + 31 – уравнение прямой;
7.3. |
x2 |
|
y2 |
1 |
– уравнение эллипса; |
7.4. |
|
x2 y2 |
16 |
– уравнение |
||||
9 |
|
|||||||||||||
|
25 |
|
|
|
|
|
|
|
|
|
|
|
||
окружности; |
7.5. |
x 3y2 |
5y 4 – уравнение параболы; 7.6. |
y |
x2 |
2x 1 |
– |
|||||||
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
уравнение параболы; 7.7. |
y 'x tg t ; 7.8. |
y 'x |
b |
ctg t ; |
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 'x |
|
2 |
|
|
|
|
b |
|
|
||||||||
|
y 'x (1 10t) 3 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
7.9. |
; 7.10. |
9t2 |
3 2t 1 2 |
; 7.11. |
|
y 'x |
a cth t |
; |
|||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
7.12. |
y ' |
|
|
t 4 4t3 2t 2 |
; 7.13. y x 2 |
, |
y x |
; 7.14. y = x+1, y = x; |
|||||||||||||||||||
x |
t 4 4t3 2t 2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
7.15. 7x+5y 35 2 0 , 5x |
7y+12 |
|
2 0 ; 7.16. 2 |
3 x+y–8=0, |
3 x |
6y+9=0; |
|
||||||||||||||||||||
7.17. y = |
x, y = x + 2; 7.18. 5x+3y+1=0, 3x |
5y |
13=0. |
|
|
|
|
|
|
|
|
||||||||||||||||
§8. Дифференциал функции
Функция y = f(x) называется дифференцируемой в точке х0 , если еѐ приращение в этой точке, соответствующее приращению аргумента ∆х, может быть представлено в виде
∆y = A·∆x+α(∆x)· ∆x,
(1)
где А – число, не зависящее от ∆x (А зависит от х0 ), α(∆x) – бесконечно малая функция при ∆x→0.
Дифференциалом этой функции в точке х0 называется главная часть еѐ приращения функции А·∆x (линейная относительно приращения аргумента). Для того чтобы функция y = f(x) была дифференцируемой в точке х0, необходимо и достаточно, чтобы существовала конечная производная f (x0 ) ;
при этом справедливо равенство A f (x0 ) . Этот факт позволяет называть дифференцируемой всякую функцию, имеющую конечную производную.
Выражение для дифференциала функции y = f(x) в точке х0 имеет вид |
|
dy(х0) = f '(х0)· ∆x. |
(2) |
Для независимой переменной х еѐ приращения совпадает |
с еѐ |
дифференциалом: ∆x = dx. Таким образом, для вычисления дифференциала
функции используют формулу |
|
dy= f '(х)· dx. |
(3) |
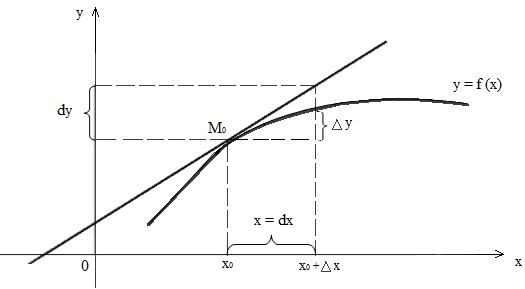
Геометрически дифференциал функции y = f(x) в точке х0 |
равен |
приращению ординаты касательной к графику этой функции в |
точке |
М0(х0; f(х0)) при приращении аргумента ∆x. |
|
37
Основные свойства дифференциала
Если с const , u = u(x) и v = v(x) – дифференцируемые функции, то:
1.dc 0
2.d(u ± v) du dv
3.d(c u) c du
4.d(u v) u dv v du
|
u |
|
v du u dv |
,(v 0) |
|||
5. |
d |
|
|
|
|
||
|
v |
2 |
|||||
|
v |
|
|
|
|||
6. Cвойство инвариантности: дифференциал функции равен произведению производной этой функции на дифференциал аргумента, при этом безразлично, будет ли аргумент независимой переменной или дифференцируемой функцией от другой независимой переменной, т.е. если u = u(x) – функция, дифференцируемая в точке x, а y = f(u) – функция, дифференцируемая в соответствующей точке u, то
dy f '(u) du f (u(x)) ' dx
Таблица дифференциалов некоторых элементарных функций
|
Пусть u = u(x) – дифференцируемая функция, тогда |
|
||
1. |
d(uα)=α·uα-1·du |
3. |
d(eu)=eu · du |
|
2. |
d(au)=au · ln a·du |
4. |
d (loga u) |
du |
|
|
u ln a |
||
|
|
|
|
|
38

5. d(ln u) duu
6. d (sin u) cosu du
7. d (cosu) sin u du
8. |
d (tgu) |
du |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||
cos2 u |
|
|
|
|
|
||||||||
9. |
d(ctgu) |
|
du |
|
|
|
|
|
|||||
sin2 u |
|
|
|||||||||||
|
|
|
|
|
|||||||||
10. d (arcsin u) |
|
|
|
du |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
1 |
u2 |
||||||||||||
|
|
|
|
||||||||||
11. d (arccos u) |
|
|
|
du |
|||||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
||||||||
1 |
u2 |
||||||||||||
|
|
|
|
|
|
|
|
||||||
12. d (arctg u) |
|
|
du |
|||||
|
|
|
|
|
|
|||
|
|
u2 |
||||||
|
|
1 |
||||||
13. d (arcctg u) |
|
du |
||||||
|
u2 |
|||||||
|
|
|
|
|
1 |
|||
14.d(sh u) = ch u · du |
||||||||
15.d(ch u ) = sh u · du |
||||||||
16. d (thu) |
du |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2 |
u |
|
|
|
|
|||
|
ch |
|
|
|
|
|||
17. d(cthu) du sh2u
Если приращение аргумента ∆х мало по абсолютной величине, то ∆y ≈ dy, т.е. f (x0+∆x) – f (x0) ≈ f '(x0 )·∆x, откуда получаем формулу для приближѐнных
вычислений значения функции в точке: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x0+∆x) ≈ f (x0) + f '(x0 )·∆x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Примеры с решениями |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2ctg |
2 |
|
|||||||
|
Пример 1. Найти дифференциал функции y 4 |
|
x3 |
|
|
log52 arccos |
|
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Решение. Воспользуемся формулой (3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
dy |
f '(x)dx |
|
3 |
x |
|
|
log52 arccos |
x |
|
|
4 |
|
|
5arccos |
x |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|||||||||||||||||||||||||
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
arccos |
|
ln 2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ctg |
2 |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
2 |
|
x ln 2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
sin2 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
54 |
|
|
x2 log42 arccos |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ctg |
|
ln 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
dy |
|
|
log52 arccos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
4 4 x |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln 2 |
4 x |
2 |
arccos |
|
x |
2 |
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
39

Пример 2. Вычислить приближѐнно 1,986.
Решение. Рассмотрим число 1,986 как конкретное значение функции y = x6 в точке х0+∆х=1,98. Возьмѐм х0=2, тогда ∆х=–0,02. Вычислим f(x0) = f(2) = 26=64. Найдем f '(x) = (x6 )'=6x5 и вычислим f '(x0) = f '(2)=6·25=6·32=192. Поставим полученные значения в формулу (4):
1,986 ≈ f(x0)+f '(x0)·∆x=64+192·(–0,02)=64–3,84=60,16. Ответ: 1,986 ≈ 60,16.
Пример 3. Найти приближенно значение объѐма V шара радиусом r =1,02 м.
Решение. Поскольку V(r) = 43 r3 , то, полагая r0 = 1, ∆r = 0,02 и используя формулу (4), получаем:
V(1,02) ≈ V(r0)+V '(r0)·∆r = V(1)+V '(1)·0,02 = 43 +4π·0,02≈4,44.
Ответ: 4,44 м 3.
Примеры для самостоятельного решения
8.1.Найти приращение ∆y и дифференциал dy функции y = x2 – 3x + 2, соответствующие значению аргумента x0=2 и двум различным приращениям аргумента (∆x)1 =0,1 и (∆x)2=0,01.
8.2.Найти приращение ∆y и дифференциал dy функции y = x3 – 2x –5, соответствующие значению аргумента х0 = –3 и приращениям аргумента
(∆x)1=0,1 и (∆x)2 =0,01.
8.3.Доказать, что для линейной функции y = kx + b приращение ∆y и дифференциал dy совпадают.
8.4.Вычислить приближѐнное значение площади круга, радиус которого равен
3,02 м.
8.5.Вычислить приближѐнное значение arcsin 0,51.
8.6.Вычислить приближѐнное значение arctg 0,98.
8.7.Вычислить приближѐнное значение 3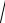 1, 02 .
1, 02 .
8.8.Вычислить приближѐнное значение 4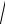 15, 968 .
15, 968 .
|
|
|
1 |
ln |
x 4 |
|
|
|
8.9. y(x) ln(x |
x2 4) |
, |
dy ? |
|||||
|
|
|||||||
|
|
|
8 x 4 |
|
|
|||
40
