
кванты лекции
.pdf1.ОСНОВЫ КЛАССИЧЕСКОЙ ТЕОРИИ ХИМИЧЕСКОГО СТРОЕНИЯ
1.1.Молекулы, ионы, свободные радикалы
Атомы элементов могут образовать три вида частиц, участвующих в химических процессах – молекулы, ионы и свободные радикалы.
Молекулой называется наименьшая нейтральная частица данного вещества, обладающая его химическими свойствами и способная к самостоятельному существованию. Различают одноатомные, двух-, трех- и т.д., в общем многоатомные молекулы. В обычных условиях из одноатомных молекул состоят благородные газы; молекулы высокомолекулярных соединений содержат многие тысячи атомов.
Ион – заряженная частица, представляющая собой атом или группу химически связанных атомов с избытком (анионы) или недостатком (катионы) электронов. В веществе положительные ионы всегда существуют вместе с отрицательными.
Свободным радикалом называется частица, обладающая ненасыщенными валентностями. Такими частицами являются, например, CH3 и NH2. В обычных условиях свободные радикалы, как правило, не могут существовать длительное время. Эти частицы играют чрезвычайно важную роль в химических процессах. Известны радикалы сложного строения (например, трифенилметил), которые являются сравнительно стабильными и могут существовать при обычных условиях.
1.2. Основные положения классической теории химического строения
Теория химического строения – теория, описывающая строение соединений (преимущественно органических), т. е. последовательность (порядок) расположения атомов и связей в молекуле, взаимное влияние атомов, а также связь строения с физическими и химическими свойствами веществ. Впервые основные положения теории химического строения были высказаны А. М. Бутлеровым в 1861 г.
Предпосылки создания теории химического строения: начало 19 в. – гравитационная теория Бергмана и Бертолле; 1810 г. – электрохимическая теория Берцелиуса; 1840-е гг. – теория типов Дюма – Жерара; 1852 г. – введено понятие валентности (Франкленд);
1857 – 58 гг. – постулирование Кекуле и Купером четырёхвалентности углерода; 1858 г. – Купером предложены графические формулы органических соединений, близкие
формулам, вытекающим из теории химического строения; 1860 г. – 1- й Международный конгресс химиков в городе Карлсруэ, установление понятий
атом и молекула (Канниццаро).
Основные положения теории химического строения заключаются в следующем:
1)в органических молекулах атомы соединяются между собой в определённом порядке согласно их валентности, что определяет химическое строение молекул;
2)химические и физические свойства органических соединений зависят как от природы и числа входящих в их состав атомов, так и от химического строения молекул;
3)для каждой эмпирической формулы можно вывести определённое число теоретически возможных структур (изомеров);
4)каждое органическое соединение имеет одну формулу химического строения, которая даёт представление о свойствах этого соединения;
5)в молекулах существует взаимное влияние атомов как связанных, так и непосредственно не связанных друг с другом. Последнее положение теории было развито учеником Бутлерова В. В. Марковниковым (правило Марковникова) и в дальнейшем – многими другими учёными.
Правильность своей теории Бутлеров подтвердил синтезом ряда органических соединений. Теория химического строения обладала огромной предсказательной способностью в направлении синтеза органических соединений и установлении строения уже известных веществ. Поэтому теория Бутлерова способствовала бурному развитию химической науки, в том числе синтетической органической химии, и химической промышленности.
Дальнейшее развитие теории химического строения обогатило органическую химию новыми представлениями, например о циклическом строении бензола (Кекуле, 1865) и осцилляции (перемещении) двойных связей в его молекуле (1872), об особых свойствах соединений с сопряжёнными связями (теория парциальных валентностей, Ф. К. И. Тиле, 1899). Развитие стереохимии привело к созданию теории напряжения (А. Байер, 1885), объясняющей различную устойчивость циклов в зависимости от их размера, и в дальнейшем – к конформационному анализу (Г. Заксе, 1890, и Э. Мор, 1918). Основные положения теории химического получили подтверждение при изучении органических соединений химическими, физическими и расчётными методами.
Фундаментальное значение в теории химического строения имеют представления о взаимном влиянии атомов в молекулах органических соединений. Однако теория химического строения не могла объяснить природу этого влияния, его внутренний механизм. Это стало возможным благодаря успехам физики, позволившим раскрыть сущность понятий «валентность»
и«химическая связь». С начала 20 в. возникают электронные представления в органической химии, в основе которых лежат электронные трактовки природы ионов (Дж. Дж. Томсон), ионной связи (В. Коссель) и ковалентной связи (И. Штарк, Г. Н. Льюис). Электронные представления позволили объяснить причину взаимного влияния атомов (статическим и динамическим смещением электронной плотности в молекуле) и предсказывать направленность реакций в зависимости от химического строения реагентов. С конца 20-х гг. 20 в. химическую связь стали трактовать с позиций квантовой химии.
Теория Бутлерова лежит в основе номенклатуры и систематики органических соединений, а применение его структурных формул помогает как определению путей синтеза новых веществ, так
иустановлению строения сложных (в т. ч. и природных) соединений.
1.3. Величины, определяющие геометрическую конфигурацию молекулы
Характеристиками геометрического строения молекул являются: длины связей, валентные углы, торсионные, или диэдральные углы. Как правило, геометрический аспект включает информацию о валентности входящих в молекулу атомов, последовательности и кратности химических связей между ними, возможных конформациях, изомерах и т.д. На основе классической теории такое представление о структуре молекул позволяет классифицировать близкие по строению структурные фрагменты по типам, проводить корреляцию свойств молекул с числами имеющихся в них структурных фрагментов определенных типов и сопоставлять свойства молекул, построенных из однотипных наборов структурных фрагментов. Наглядно при таком подходе молекулу в каждом состоянии можно изобразить либо системой (колеблющихся) материальных точек, либо в общем случае системой перекрывающихся сфер, радиусы которых задаются по определенным правилам.
1.3.1. Длина химической связи
Длина химической связи – расстояние между ядрами химически связанных атомов. Длина химической связи – важная физическая величина, определяющая геометрические размеры химической связи, её протяжённость в пространстве. Для определения длины химической связи используют различные методы. Газовую электронографию, микроволновую спектроскопию, спектры комбинационного рассеяния и ИК-спектры высокого разрешения применяют для оценки длины химических связей изолированных молекул в паровой (газовой) фазе. Межъядерные расстояния в кристаллах определяют с помощью рентгеноструктурного анализа, нейтронографии и электронографии.
Приближенно длина химической связи является аддитивной величиной, определяемой суммой ковалентных радиусов атомов, составляющих химическую связь. Однако, длина химической связи (dAB) между электроотрицательным и электроположительным атомами несколько короче, чем длина, полученная сложением ковалентных радиусов элементов (rA и rB),
2
составляющих молекулу. Поправка на отклонение от принципа аддитивности ковалентных радиусов учитывается уравнением Шомакера – Стивенсона:
dAB = rA + rB − 0,09(χA − χB ) |
(1) |
и составляет величину k = 0,09 χ, где χ – разность значений электроотрицательностей атомов χA и χB.
1.3.2. Валентный угол
Валентный угол – угол, образованный направлениями химических связей, исходящими из одного атома. Валентные углы зависят как от индивидуальных особенностей присоединенных атомов, так и от гибридизации атомных орбиталей центрального атома. Для простых молекул валентный угол, как и другие геометрические параметры молекулы, можно рассчитать методами квантовой химии. Экспериментально их определяют из значений моментов инерции молекул, полученных путем анализа их вращательных спектров. Валентный угол сложных молекул определяют методами дифракционного структурного анализа.
Очень простой способ предсказания валентных углов был разработан Гиллеспи. В его основе лежит модель отталкивания локализованных электронных пар.
Предполагается, что каждая пара электронов, окружающих данный атом, обозначаемая в льюисовских формулах двумя точками, образует электронное облако, причем вследствие отталкивания облака располагаются так, чтобы быть возможно дальше друг от друга. В первом приближении можно считать отталкивание всех облаков одинаковыми, тогда в зависимости от их числа они будут располагаться следующим образом.
Число и расположение электронных облаков
2линейное (BeCl2)
3треугольник (BCl3)
4тетраэдр (P4)
5тригональная бипирамида (PCl5)
6октаэдр (SF6)
7семивершинник (IF7)
Расположение атомов будет иметь иную конфигурацию, если в молекуле имеются электронные пары, не образующие связь, – неподеленные пары. Так, при тетраэдрическом расположении четырех электронных пар вокруг атома азота в молекуле аммиака эта молекула имеет пирамидальное строение, т.к. одна вершина в тетраэдре занята не атомом, а неподеленной парой.
Описанная модель может быть уточнена тремя дополнениями: 1) электронное облако двойной связи занимает большее пространство, чем облако одинарной связи; 2) электронное облако неподеленной пары занимает большее пространство, чем облако связующей пары (т.к. последнее в значительной степени сосредоточено между атомами); 3) чем более электроотрицателен атом-партнер, тем меньшее пространство вблизи последнего требуется для электронной пары (т.к. она оттянута к атому-соседу).
1.3.3. Торсионный угол
Торсионный угол – двугранный угол между двумя плоскостями, проходящими через какие- либо выделенные ядра. В четырехатомных молекулах атомы могут располагаться по прямой (как, например, в случае ацетилена), в одной плоскости (как в случае формальдегида или трифторида бора) или в трехмерном пространстве (как в случае молекулы аммиака). Различными по своему характеру (также линейными или с наличием разветвлений) могут быть и структурные отношения между атомами. При этом для описания линейных четырехатомных индивидуальных молекул (или четырехатомных фрагментов А– В– С–D, входящих в состав более сложных цепных систем) и
3
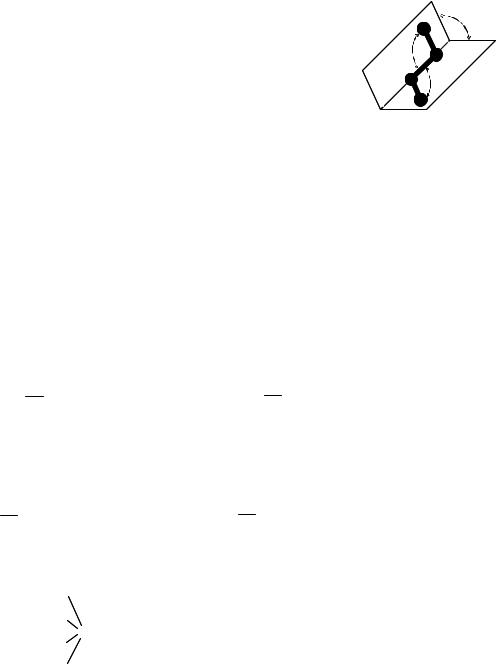
применяют торсионный угол τ (рис. 1). Этот угол фактически отражает характер взаимного расположения двух трехъядерных фрагментов (А– В– С и В– С–D) четырехатомной молекулы, которые характеризуются своими собственными величинами валентных углов θ1 и θ2. Наиболее наглядно двугранные углы изображаются в ньюменовских проекциях, при построении которых молекула рассматривается вдоль направления связи В– С, через которую проведен воображаемый диск (ближняя связь А– В при этом видна со стороны наблюдателя, а дальняя связь С–D проглядывается из-за этого диска).
1.4. Структурная формула и граф молекулы
|
D |
τ |
|
θ2 |
|
C |
|
B |
θ1 |
||
|
|||
|
|
||
A |
|
|
Рис. 1. К определению торсионного угла.
Структурная формула – это разновидность химической формулы, графически описывающая расположение и порядок связи атомов в соединении, выраженное на плоскости. Связи в структурных формулах обозначаются валентными черточками. Эмпирические формулы, в отличие от структурных, показывают только, какое число атомов каждого элемента входит в молекулу.
Обычно для изображения строения молекул применяют упрощенные структурные формулы, в которых связи с атомами водорода не показывают валентными черточками. Таким образом, строение двух изомерных веществ эмпирической формулы С4Н10 может быть сокращенно выражено следующими формулами:
CH3 |
CH2 |
|
CH2 |
|
CH3 |
CH3 |
CH |
|
CH3 |
|
|
|
|||||||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
CH3
При выводе возможных структурных формул следует иметь в виду, что эти формулы изображают только порядок связи атомов, а не пространственное их расположение и что поэтому формулы
CH3 |
|
CH |
|
CH2 |
|
CH3 |
CH3 |
CH2 |
|
|
CH |
|
CH3 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
||||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||
|
|
CH3 |
|
|
|
CH3 |
|||||||
выражают одно и то же строение вещества. Изображения
CH3 |
|
|
|
|
|
CH3 |
||
CH3 |
C |
|
CH |
|
|
|
|
CH |
и |
|
C |
|
|||||
|
|
|
||||||
CH3 |
|
|
3 |
|
3 |
|||
|
|
|
|
|
|
|
|
|
CH |
|
|
|
|
|
CH3 |
||
3 |
|
|
|
|
|
|
|
|
выражают также одно и то же вещество с одним и тем же химическим строением.
С помощью разных типов условных обозначений, используемых в структурных формулах, указываются также координационные связи, водородные связи, стереохимия молекул, делокализованные связи, локализация зарядов и т. д.
Скелетная формула органических соединений – формула, изображающая структурную формулу органического соединения в «свёрнутом» виде, не отображающим связи углерод-водород, а также атомы водорода и углерода. На атом углерода указывает излом цепи или ее окончание, если к нему не присоединена какая-либо не углеводородная группа. Скелетные формулы органических соединений являются сокращенным представлением молекулярной структуры, они широко распространены в органической химии, поскольку они чётко показывают сложные структуры органических соединений.
Для обозначения направленности связей в пространстве для них используют следующие обозначения:
1)прямые линии – связи, лежащие в одной плоскости;
2)клинообразные линии – связи, направленные вверх относительно плоскости, т.е. к наблюдателю;
4
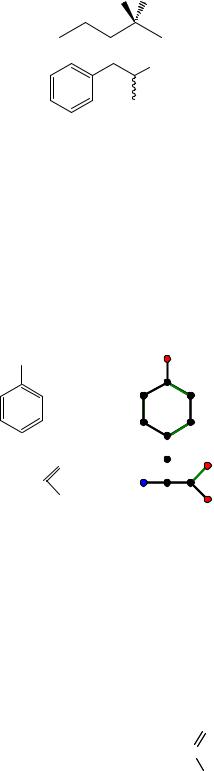
3)пунктирные клинообразные линии – связи, направленные вниз относительно плоскости, т.е. от наблюдателя;
4)волнообразные линии обозначают или неизвестную стереохимию или эквимолярную смесь пары энантиомеров (оптических изомеров).
Примерами могут служить скелетные формулы 2-фтор-2-хлорпентана
F Cl
и амфетамина, который является рацематом
NH2
Молекулярный граф – связный неориентированный граф, находящийся во взаимно- однозначном соответствии со структурной формулой химического соединения таким образом, что вершинам графа соответствуют атомы молекулы, а рёбрам графа – химические связи между этими атомами. Это абстрактная модель, отображающая топологию молекулы. Понятие «молекулярный граф» является базовым для компьютерной химии и хемоинформатики. Как и структурная формула, молекулярный граф является моделью молекулы, и как всякая модель, он отражает далеко не все свойства прототипа. В отличие от структурной формулы, где всегда указывается, к какому химическому элементу относится данный атом, вершины молекулярного графа могут быть непомеченными – в этом случае молекулярный граф будет отражать только структуру, но не состав молекулы. Точно так же рёбра молекулярного графа могут быть непомеченными – в таком случае не будет делаться различие между ординарными и кратными химическими связями. В некоторых случаях может использоваться молекулярный граф, отражающий только углеродный скелет молекулы органического соединения.
OH
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
CH2 |
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H2N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
H |
|
OH |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Базовые определения теории графов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1) Степень вершины – количество инцидентных ей ребер; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2) Вершина называется изолированной, если она не является концом ни для одного ребра; |
|||||||||||||||||||||||||||||||
|
или листом, если она является концом ровно одного ребра; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
3) |
Путь (или цепь) в графе |
– конечная последовательность |
вершин, |
в |
которой |
каждая |
|||||||||||||||||||||||||
|
вершина (кроме последней) соединена со следующей в последовательности вершин |
||||||||||||||||||||||||||||||
|
ребром; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) Цикл – |
путь, в котором первая и последняя вершины совпадают. Длина пути (или цикла) – |
||||||||||||||||||||||||||||||
|
число составляющих его ребер; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
5) |
Дерево – связный граф, |
не содержащий |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
3 |
4 |
5 |
|
6 |
|
7 |
|
|||||||||||
|
простых циклов; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
1 |
|
0 |
1 |
1 |
|
1 |
|
0 |
|
||
6) |
Подграф – граф, содержащий поднабор |
|
|
|
|
4 |
3 |
|
|
|
|
|
|
||||||||||||||||||
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
вершин и ребер другого графа. |
|
|
|
|
|
|
O |
|
2 |
1 |
|
0 |
|
1 |
0 |
0 |
|
0 |
|
1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
5 |
|
|
1 |
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
0 |
0 |
0 |
|
0 |
|
0 |
|
|||||||
Уровень |
абстрагирования |
теории |
|
графов |
H |
|
C |
|
|
C |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||
удобен для вычислительного решения широкого |
|
|
|
|
6 |
|
H 7 |
|
4 |
1 |
|
0 |
|
0 |
0 |
0 |
|
0 |
|
0 |
|
||||||||||
круга |
химических |
задач. |
|
Естественным |
|
|
H |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
1 |
|
0 |
|
0 |
0 |
0 |
|
0 |
|
0 |
|
|||||||||||||
|
|
|
n = 7 |
|
|
|
|
|
|
||||||||||||||||||||||
расширением |
молекулярного |
графа |
является |
|
|
|
6 |
1 |
|
0 |
|
0 |
0 |
0 |
|
0 |
|
0 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
реакционный граф, рёбра которого соответствуют |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
0 |
|
1 |
|
0 |
0 |
0 |
|
0 |
|
0 |
|
||||||||||||
образованию, разрыву и изменению порядка |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
связей между атомами. |
Для решения различных |
Рис. 2. Матрица смежности для графа молекулы |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ацетальдегида. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
5
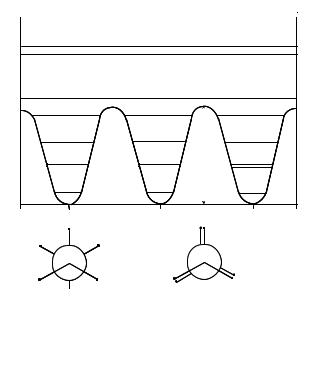
задач методами компьютерной химии молекулярный граф представляют в виде матрицы. Одним из способов является построение матрицы смежности. В качестве примера на рис. 2 изображена матрица смежности для графа молекулы ацетальдегида.
Для молекулы, состоящей из n атомов, составляется матрица размерности n × n . При этом атомы нумеруются произвольно. Элементами матрицы являются aij = 1, если между атомами i и j имеется химическая связь, и aij = 0, если между атомами i и j нет химической связи. Применяют и другие матричные формы представления молекулярных графов. Элементами матриц могут служить длины связей и топологические расстояния (число связей по кратчайшему пути).
1.5. Внутреннее вращение и конформации молекул
Внутреннее вращение молекулы – вращение фрагментов молекулы относительно друг друга вокруг соединяющей их химической связи. Обусловливает возникновение различных конформаций молекулы, характеризуемых определенными значениями потенциальной энергии. Последняя меняется периодически при изменении угла относительного поворота τ фрагментов молекулы (волчков) и описывается потенциальной функцией внутреннего вращения U(τ). Максимумы потенциальных кривых (см. рис. 3) соответствуют нестабильным конформациям, минимумы – стабильным. Высота максимума по отношению к соседнему минимуму называется потенциальным барьером внутреннего вращения U0. В зависимости от соотношения значений U0 и тепловой энергии молекул, равной kT (k – постоянная Больцмана, Т – абсолютная температура), различают свободное внутреннее вращение, когда U0 << kТ (например, вращение метильных групп в СН3С≡ССН3), и заторможенное внутреннее вращение, когда U0 ≈ kT (например, в С2Н6, для которого U0 = 12,5 кДж/моль). При U0 >> kT внутреннее вращение отсутствует, как, например, в молекуле СН2=СН2 при обычных температурах. При свободном внутреннем вращении любые относительные ориентации вращающихся групп (т.е. все конформации) практически равновероятны. При заторможенном внутреннем вращении и его отсутствии существуют преимущественно стабильные конформации, причем в первом случае между ними осуществляются конформационные переходы, а во втором нет. Появление потенциального барьера внутреннего вращения вокруг одинарной связи приближенно можно объяснить невалентными взаимодействиями атомов вращающихся фрагментов, природа которых та же, что и у межмолекулярного взаимодействия.
|
|
|
|
|
Число максимумов (и минимумов) |
|||||||||
|
|
|
|
|
потенциальной |
функции |
|
внутреннего |
||||||
|
|
|
|
A |
вращения для τ в пределах от 0 |
до 2π (т.е. |
||||||||
|
|
|
|
кратность |
барьера |
n |
= 2π/l, |
где |
l – |
период |
||||
|
|
|
5 |
A |
||||||||||
|
|
|
E |
функции) зависит от природы атомов, |
||||||||||
|
|
|
|
|||||||||||
U(τ) |
|
|
4 AE |
связывающих |
вращающиеся |
фрагменты |
||||||||
|
|
|
A |
молекулы, |
числа |
и |
кратности |
образуемых |
||||||
|
|
|
3 E |
каждым из этих атомов связей и от валентных |
||||||||||
|
|
|
2 AE |
|||||||||||
|
|
U0 |
углов. Так, для молекулы Н2О2 барьер |
|||||||||||
|
|
1 |
A |
двукратный, |
для |
С2Н6 – |
трехкратный, |
для |
||||||
|
|
|
|
E |
CH3BF2 – шестикратный. Чем выше порядок |
|||||||||
|
|
|
τ0 |
E |
||||||||||
|
|
|
связи, вокруг которой происходит вращение, |
|||||||||||
– π |
0 |
+π |
A |
|||||||||||
|
|
тем больше величина U0. Общее выражение |
||||||||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
U(τ) можно представить рядом Фурье: |
|
|
|||||||
|
|
|
|
|
U (τ ) = a0 + ∑amcosnmτ , |
|
|
(2) |
||||||
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
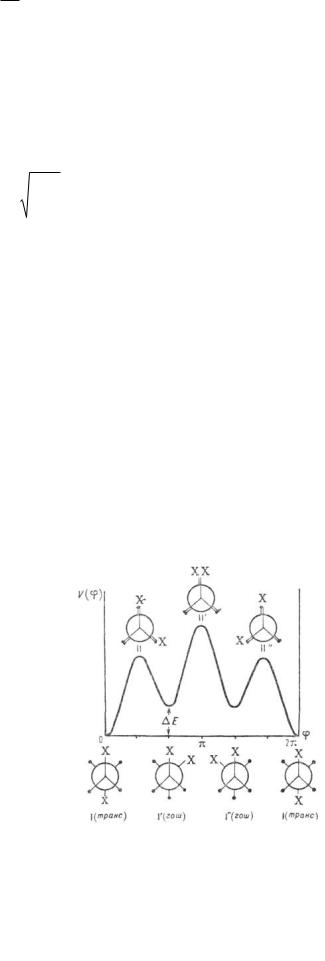
Рис. 3. Потенциальная функция и уровни энергии |
|
|
где а0, am – |
коэффициенты, m = 1,2,3... В случае |
||||||||||
|
|
симметричного |
трехкратного |
|
барьера |
|||||||||
заторможенного внутреннего вращения для молекул, |
|
|
||||||||||||
I |
|
II |
|
|
(например, |
когда |
волчок |
– |
группа |
СН3, |
||||
подобных этану. I – |
стабильные заторможенные |
|
|
|||||||||||
(шахматные) конформации, II – |
заслоненные |
|
|
имеющая поворотную ось симметрии 3-го |
||||||||||
нестабильные конформации. |
|
|
|
порядка С3) n = 3, и при |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
m = 1U (τ ) = U0 (1 − cos3τ ) , 2
т.е. U(τ) описывает положение минимумов (U = 0) и максимумов (U = U0) потенциальной кривой; последующие члены ряда будут уточнять лишь ее форму (крутизну). Решение соответствующей квантовомеханической задачи при заданном виде U(τ) в принципе позволяет найти набор энергетических уровней для заторможенного внутреннего вращения (рис. 3).
Термин «вращение» не является строгим и исчерпывающим. При высоких барьерах в нижней части потенциальных ям система уровней энергии больше соответствует колебательному характеру движения и может быть описана даже в приближении гармонического осциллятора. Частота крутильного колебания связана с U0 приближенной формулой:
ν = |
n |
|
U0 |
, |
(3) |
|
2π 2Iпр |
||||||
кр |
|
|
||||
|
|
|
||||
где Iпр = (I1I2)/(I1 + I2) – приведенный момент инерции (I1 и I2 – |
моменты инерции групп атомов, |
|||||
вращающихся одна относительно другой). Более строгое решение приводит к появлению полносимметричного А и вырожденного E подуровней, относящихся к данному значению колебательного квантового числа N, причем расщепление, показанное на рис. 3 заштрихованными областями, отражает вращательный характер внутримолекулярного движения. При больших U0 и малых N расщепление А-Е пренебрежимо мало, но по мере приближения к вершине барьера (увеличении N) это расщепление (или роль вращения) возрастает. Выше барьера расстояния между подуровнями А и Е с одним и тем же значением N становятся даже намного больше, чем между заштрихованными областями решений с разными N, т.е. полностью преобладает вращение. При U0 ≈ 0 квантовомеханическая задача решается так же, как для свободного ротатора:
Eвр = |
h2 |
|
J (J + 1) , |
(4) |
8π 2 I |
|
|||
|
|
пр |
|
|
где J – вращательное квантовое число.
При отсутствии осевой симметрии волчков, например в молекулах 1,2-дизамещенных этана, заторможенное внутреннее вращение приводит к явлению поворотной изомерии, представляющей собой частный случай конформационной изомерии, когда устойчивым конформациям соответствуют разные по глубине минимумы потенциальной энергии, т. е. возникают
различающиеся по форме и свойствам поворотные |
|
|||||||
изомеры (конформеры). В частности, у молекул типа 1,2- |
|
|||||||
дизамещенных этана имеются три стабильных |
|
|||||||
конформации – |
одна транс- (или анти-) и две гош- |
|
||||||
конформации (см. рис. 4). Относительная стабильность |
|
|||||||
поворотных изомеров определяется разностью их |
|
|||||||
энергий |
E, |
т.е. разностью значений энергии в |
|
|||||
минимумах потенциальной кривой. Например, транс- |
|
|||||||
изомер 1,2-дихлорэтана более устойчив, чем гош-изомер, |
|
|||||||
т.к. его энергия (в газовой фазе) ниже на ~ 5,6 кДж/моль. |
|
|||||||
При достаточно низких |
потенциальных барьерах |
|
||||||
(несколько десятков кДж/моль) поворотные изомеры |
|
|||||||
находятся в термодинамическом равновесии, положение |
|
|||||||
которого зависит от температуры, давления и природы |
|
|||||||
среды. |
|
|
|
|
|
|
|
|
Внутреннее вращение молекул возможно в газовой |
Рис. 4. Потенциальная функция |
|||||||
и жидкой фазах, параметры U(τ) зависят от характера |
||||||||
внутреннего вращения молекул типа |
||||||||
среды и электронного состояния молекулы. В кристаллах |
1,2-дизамешенного этана. I – I'' – |
|||||||
внутреннее вращение, |
как |
правило, отсутствует |
и |
поворотные изомеры (конформеры), |
||||
стабилен |
лишь |
один |
конформер; иногда |
существуют |
или стабильные заторможенные |
|||
конформации, II – II" – нестабильные |
||||||||
твердые |
фазы |
(например, |
у некоторых |
фреонов), |
в |
|||
заслоненные конформации. |
||||||||
которых стабильны разные конформеры и между ними
7
осуществляются переходы.
Явления заторможенного внутреннего вращения и поворотной изомерии молекул оказывают влияние на термодинамические, электрические, оптические и др. свойства веществ. Внутреннее вращение необходимо учитывать при расчете термодинамических функций методами статистической термодинамики. Например, для CH3SH опытное значение энтропии составляет 251,7 Дж/(моль·К), а расчетное (без учета внутреннего вращения) на 8,4 Дж/(моль·К) меньше. С другой стороны, если исходить из предположения о свободном внутреннем вращении, расчетная величина энтропии превышает опытную на 2,0 Дж/(моль·К); следовательно, в молекуле CH3SH существует заторможенное внутреннее вращение вокруг связи С–S.
В случае поворотной изомерии свойства вещества определяются как свойства равновесной смеси изомеров и зависят от внешних условий, влияющих на положение равновесия. Например, эффективный дипольный момент μ зависит от температуры. Если μ поворотных изомеров различны, как, например, у транс- (μ = 0) и гош- (μ ¹ 0) конформеров 1,2-дихлорэтана, то при изменении температуры значение измеряемого μ будет приближаться к значению, характерному для изомера, концентрация которого будет при этом возрастать. В жидкой фазе и в среде полярных растворителей повышается устойчивость более полярного гош-изомера в результате взаимодействия молекул растворителя и растворенного вещества. Поворотные изомеры, имея различные равновесные конфигурации, различаются своими колебательными и вращательными спектрами. При увеличении числа осей внутреннего вращения в молекуле возрастает и число ее возможных конформаций.
Представления, связанные с внутренним вращением и поворотной изомерией молекул, применяют в теории строения как низкомолекулярных, так и высокомолекулярных соединений. Разработаны методы и схемы конформационных расчетов достаточно сложных молекулярных систем на основе механических моделей, получили также развитие полуэмпирические и неэмпирические квантовомеханические расчеты потенциальных функций внутреннего вращения молекул. Для изучения явлений внутреннего вращения и поворотной изомерии молекул используют методы спектроскопии: ИК, КР, микроволновой, УФ, ЯМР, ЭПР, а также методы газовой электронографии, поглощения ультразвука, некогерентного, неупругого рассеяния нейтронов, измерения дипольных моментов, диэлектрических потерь и др.
8
2.МЕХАНИЧЕСКАЯ МОДЕЛЬ МОЛЕКУЛЫ
Вклассической теории молекула представляется в виде изолированной системы, состоящей из набора атомов, совершающих колебания относительно положений равновесия. Атомы аппроксимируют материальными точками определенной массы (т.е. электронно-ядерное строение атома игнорируется), которые несут некоторые электрические заряды и удерживаются вместе валентными и невалентными взаимодействиями. Силы, действующие в молекуле, для валентных взаимодействий (химических связей) имитируются пружинками, жесткость которых зависит от сорта атомов, которые они соединяют, а для остальных пар атомов – различными потенциалами взаимодействия. Принимают, что энергии парных атомных взаимодействий переносимы из одной молекулы в другую и аддитивны. Перечисленные приближения лежат в основе механической модели молекулы.
2.1. Поверхность потенциальной энергии
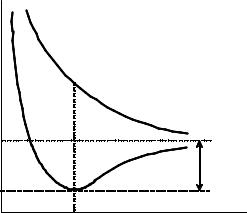
Пространственная структура молекулы определяется числом входящих в нее N атомов и их декартовыми координатами q1, q2,…, qi. Потенциальная энергия молекулы U(q1, q2,…, qi) является многомерной функцией этих координат, каждой точке которой отвечает определенная пространственная геометрическая конфигурация ядер; эту функцию называют поверхностью потенциальной энергии (ППЭ). В простейшем случае двухатомной молекулы (N = 2, молекула линейна, 3N – 5 = 1) единственной координатой является межатомное расстояние. ППЭ в данном
случае представляет собой просто одномерную |
|
|
|
|
кривую. Эта кривая, изображенная на рис. 5, может |
U |
|
|
|
быть двух основных типов: а) кривая с минимумом; |
|
|
|
|
б) кривая без минимума. В первом случае, в |
|
|
|
|
интервале r0 < r < ∞ энергетическая кривая имеет |
|
|
|
|
так называемый аттрактивный характер (энергия |
|
б |
|
|
уменьшается при сближении частиц), т.е. описывает |
|
|
|
|
притяжение. Точке r0 соответствует минимум |
|
|
|
|
энергии, и эта точка отвечает устойчивой |
|
|
|
|
геометрической конфигурации. На участке 0 < r < |
|
a |
DAB |
|
r0 |
кривая имеет репульсивный характер, энергия |
|
|
|
|
|
|
||
возрастает при сближении частиц. |
|
|
|
|
|
Кривая типа б) имеет репульсивный характер |
r0 |
|
rAB |
во |
всей области изменения r. Она не имеет |
|
||
|
|
|||
минимума, т.е. для данного состояния двух частиц |
Рис. 5. |
Примеры потенциальных кривых. |
|
не существует их устойчивого соединения. Кривая |
|||
|
|
б) реализуется, например, для взаимодействия двух одинаково заряженных ионов. Такой же тип энергетической кривой может реализовываться и для устойчивой молекулы при переходе в одно из ее высших электронных состояний. Состояния, описываемые кривой б), часто называют диссоциативными.
Четырехмерную ППЭ трехатомной системы уже нельзя представить графически, ее расчет и представление ведут обычно методом сечений. Основная проблема построения ППЭ многоатомной системы заключается в том, что для сколько-нибудь полного ее представления необходимо провести огромное количество расчетов. Если по каждой координате осуществлять m расчетов, то общее их количество будет m3N-6. Никакие суперсовременные компьютеры не смогут проделать такие расчеты даже для сравнительно небольших (~10) m и N. К счастью, для большинства практических целей нет необходимости знать функцию U(q1, q2,…, q3N-6) в полном объеме. Достаточно располагать сведениями лишь об определенных участках ППЭ, прежде всего соответствующих особым точкам, а именно максимумам и седловым точкам.
ППЭ молекулы обладает следующими свойствами: 1) ППЭ непрерывна и дважды дифференцируема.
9
2) На ППЭ обязательно имеется стационарная точка глобального (наиболее глубокого) минимума, отвечающая минимальной по энергии равновесной пространственной атомной конфигурации молекулы. Кроме этого на ППЭ могут также быть локальные минимумы, соответствующие другим стабильным конфигурациям с более высокими энергиями. В стационарных точках ППЭ
∂U = ∂U = K= |
∂U |
|
= 0. |
(5) |
||
∂q |
|
|||||
∂q |
∂q |
2 |
−6 |
|
||
1 |
|
3N |
|
|||
3) Кратчайшие пути переходов между локальными минимумами проходят через |
||||||
стационарные седловые точки ППЭ, играющие роль энергетических барьеров. |
|
|||||
Стационарной точкой некоторой |
скалярной |
функции называется точка, |
в которой |
|||
производная этой функции по рассматриваемым переменным обращается в ноль. Тип стационарной точки (максимум, минимум или седловая точка) определяется матрицей вторых производных функции, которая называется матрицей Гессе или гессианом:
|
|
|
|
|
|
|
∂2U |
|
|
|
∂2U |
|
|
|
L |
|
∂2U |
|
|
||||||
|
|
|
|
|
|
|
∂q2 |
|
|
|
∂q ∂q |
2 |
|
|
∂q ∂q |
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
1 3N −6 |
|
|
||||
H ( f ) = |
|
∂2U |
|
= |
|
∂2U |
|
|
|
∂2U |
|
|
|
L |
|
|
∂2U |
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
∂q2∂q1 |
|
|
|
∂q22 |
|
|
|
∂q2∂q3N −6 |
. |
(6) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
∂qi∂q j |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
M |
|
|
|
|
M |
|
|
|
|
O |
|
M |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
∂2U |
|
|
|
∂2U |
|
|
|
L |
|
∂2U |
|
|
|
|||||
|
|
|
|
|
|
∂q |
|
∂q ∂q |
∂q |
2 |
|
∂q2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
3N −6 |
|
1 |
|
|
3N −6 |
|
|
|
|
|
|
3N −6 |
|
|
||||
Элементы матрицы есть вторые производные энергии U по координатам ядер атомов. Всегда |
|||||||||||||||||||||||||
возможно эквивалентное преобразование этой матрицы к диагональному виду |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
f1 |
|
0 |
L |
|
0 |
|
|
|
|
|
|
|
|
|
|||
|
|
H ( f ) = |
0 |
|
f2 |
L |
|
0 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
M |
|
M |
O |
|
M . |
|
|
|
|
|
(7) |
||||||||||||
0 0 L f3N −6
По физическому смыслу гессиан представляет собой матрицу силовых постоянных молекулы, которая в гармоническом приближении определяет энергии и частоты нормальных колебаний ядер. В минимуме ППЭ все элементы матрицы Гессе, приведенной к диагональному виду, положительны, а в седловых точках имеется один или несколько отрицательных элементов. Это выглядит так, как будто энергии некоторых колебаний отрицательны, а соответствующие колебательные частоты являются мнимыми. Число мнимых частот определяет вид стационарной точки, с которой соотносится данная молекулярная структура; точка, имеющая n мнимых частот, является седловой точкой n-го порядка. Энергетическим барьерам ППЭ отвечают седловые точки первого порядка: они имеют отрицательную кривизну вдоль кратчайших путей
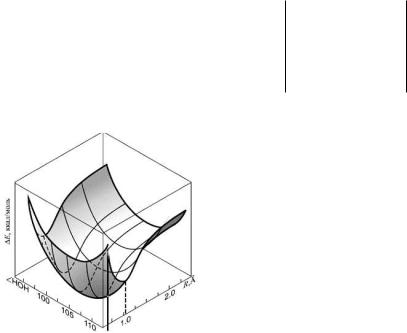
Рис. 6. ППЭ молекулы воды. перехода между локальными минимумами и положительные значения кривизны вдоль направлений, перпендикулярных
этим путям. В качестве примера на рис. 6 изображена ППЭ молекулы воды.
2.2. Основные составляющие потенциальной энергии молекулы
Изменение положений атомов приводит к различным пространственным структурам молекулы. Если при этом система валентных связей сохраняется, все эти структуры составляют множество конформаций молекулы. Исследование множества стабильных пространственных структур молекулы и путей переходов между ними составляют предмет конформационного анализа. Выборочным методом находят конформации молекулы, приблизительно отвечающие
10
