
кванты лекции
.pdf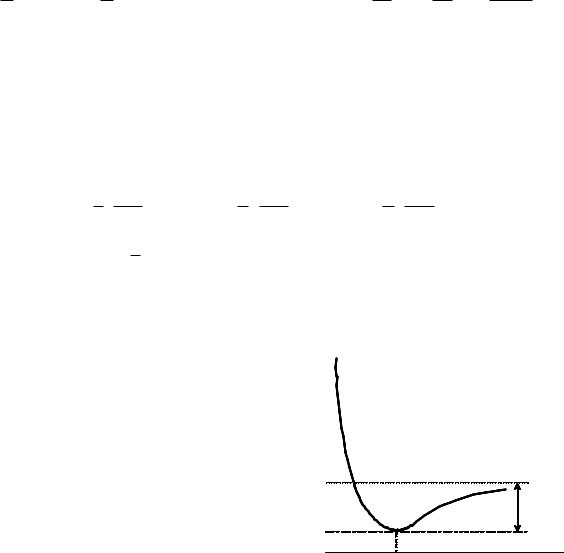
локальным минимумам, а затем, минимизируя энергию молекулы путем изменения координат |
||||||||||||||||||||||||||||||||||||||||||||||||||
атомов, находят энергетически предпочтительные стабильные атомные геометрии. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
Для механической модели молекулы данная задача решается следующим образом. Прежде |
|||||||||||||||||||||||||||||||||||||||||||||||||
всего, от декартовых координат переходят к так называемым внутренним координатам молекулы, |
||||||||||||||||||||||||||||||||||||||||||||||||||
в которых каждый атом описывается по отношению к другим атомам. Внутренние координаты |
||||||||||||||||||||||||||||||||||||||||||||||||||
представляют собой набор всех длин связей, углов между векторами (валентных углов) и |
||||||||||||||||||||||||||||||||||||||||||||||||||
торсионных углов. Преимущество внутренних координат, число которых равно 3N–6, |
в том, что в |
|||||||||||||||||||||||||||||||||||||||||||||||||
них хорошо видно, что колебательное движение атомов сохраняет атомную пространственную |
||||||||||||||||||||||||||||||||||||||||||||||||||
структуру молекулы. Потенциальная энергия молекулы записывается как параметрическая |
||||||||||||||||||||||||||||||||||||||||||||||||||
функция внутренних координат атомов следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U = Uсв + Uугл + Uторс + Uневал |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(8) |
|||||||||||||
Здесь Uсв, |
Uугл и Uторс – вклады в потенциальную энергию, связанные с изменением межъядерных |
|||||||||||||||||||||||||||||||||||||||||||||||||
расстояний для пар атомов, образующих валентные химические связи, при их растяжении и |
||||||||||||||||||||||||||||||||||||||||||||||||||
сжатии, и при деформации валентных и торсионных углов, соответственно; Uневал объединяет |
||||||||||||||||||||||||||||||||||||||||||||||||||
вклады в потенциальную энергию, связанные с различными невалентными взаимодействиями. |
||||||||||||||||||||||||||||||||||||||||||||||||||
Простейшее уравнение для потенциальной энергии молекулы (уравнение силового поля) имеет |
||||||||||||||||||||||||||||||||||||||||||||||||||
вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ ij |
|
12 |
|
|
σ ij |
|
6 |
|
|
|
|
|
|
|
|||
|
U = |
|
|
k |
|
|
2 |
|
|
k |
|
(θ |
|
− θ |
|
|
2 |
a cosnmτ + |
|
N |
N |
|
|
|
|
|
− |
|
|
|
+ |
qi q j |
|
|
(9) |
|||||||||||||||
|
∑ |
|
i |
(r − r ) |
+ |
∑ |
|
|
i |
i |
0 |
) + |
∑∑ |
4ε |
ij |
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||||||||
|
|
2 |
i |
0 |
|
|
2 |
|
|
|
|
|
∑ i |
|
|
|
|
|
|
|
r |
|
|
|
|
r |
|
|
|
4πε |
r |
|
|
|
||||||||||||||||
|
|
св |
|
|
|
угл |
|
|
|
|
|
|
|
|
торс |
|
|
|
|
i =1 j =i +1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ij |
|
|
|
|
ij |
|
|
|
|
|
0 ij |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Рассмотрим компоненты потенциальной энергии более детально. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
2.2.1. Потенциальная энергия растяжения и сжатия связей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
В силу принятого приближения аддитивности парных атомных взаимодействий, представим |
|||||||||||||||||||||||||||||||||||||||||||||||||
энергию растяжения и сжатия связи между парой атомов А и В в виде разложения потенциальной |
||||||||||||||||||||||||||||||||||||||||||||||||||
энергии двухатомной молекулы АВ Uсв(rAB) в ряд Тейлора относительно точки равновесия, |
||||||||||||||||||||||||||||||||||||||||||||||||||
отвечающей минимуму потенциальной энергии: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
(rAB |
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
1 |
|
4 |
|
|
(rAB |
|
|
|
|
|
|
||||||||
|
Uсв (rAB ) = U (r0 ) + |
d U |
|
2 |
+ |
d U |
|
|
|
|
|
3 |
|
d U |
|
4 |
+ |
K |
= |
|
||||||||||||||||||||||||||||||
|
2 |
|
dr |
2 |
|
− r0 ) |
3! |
|
dr |
3 |
|
(rAB − r0 ) |
|
+ |
|
|
|
dr |
4 |
− r0 ) |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
4! |
|
r |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= U (r ) + 1 k |
|
|
|
(r |
− r )2 |
+ β |
|
(r |
|
− r )3 |
+ γ |
|
|
|
(r |
|
− r )4 |
+ K |
|
|
|
|
|
|
|
(10) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
2 |
AB |
AB |
0 |
|
|
AB |
AB |
|
0 |
|
AB |
|
|
AB |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
(rAB – |
межъядерное расстояние в произвольный момент времени). Здесь учитывается, что в точке |
|||||||||||||||||||||||||||||||||||||||||||||||||
минимума первая производная потенциальной энергии по смещению равна нулю. Выбором |
||||||||||||||||||||||||||||||||||||||||||||||||||
постоянной можно регулировать начало отсчета энергии. Параметры kAB, βAB и γAB характеризуют |
||||||||||||||||||||||||||||||||||||||||||||||||||
взаимодействие атомов А и В; они называются |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
силовыми постоянными. Параметр kAB = 400 – 900 |
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
ккал/моль описывает жесткость связи АВ так, как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
будто эти атомы соединены упругой пружиной и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
колеблются гармонически. Обычно смещения атомов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
составляют |
~ |
|
0,1 |
Å |
и |
гармоническое |
приближение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
оправдано. К сожалению, при больших отклонениях |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
от |
равновесия |
энергия |
|
|
растяжения |
|
связи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
нереалистично возрастает; поэтому в ряде случаев |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
необходимо |
|
учитывать |
|
ангармонический |
характер |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DAB |
|
|||||||||||||||||||||||
колебаний и вводить ангармонические силовые |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
постоянные βAB < 0 и γAB > 0. |
|
|
функция, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Имеется |
|
|
аналитическая |
|
хорошо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rAB |
|||||||||||||||||||||||
аппроксимирующая кривую в двухатомных молекулах |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
Рис. 7. Зависимость между потенциальной |
|
||||||||||||||||||||||||||||||||||||||||||||||||
и позволяющая получить точное решение квантово- |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
энергией связи и расстоянием, описанная с |
|
||||||||||||||||||||||||||||||||||||||||||||||||
механического |
|
|
уравнения |
|
|
Шредингера |
|
для |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
помощью функции Морзе. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
11
колебательного движения. Речь идет о потенциале Морзе:
U (r |
− r ) = D |
[e−2α AB ( rAB − r0 ) − 2e−aAB ( rAB −r0 ) ]. |
(11) |
|
AB |
0 |
AB |
|
|
Здесь DAB – энергия диссоциации молекулы, αAB – параметр связи АВ, характеризующий крутизну |
||||
склонов потенциальной ямы (см. рис. 7). |
|
|
||
Раскладывая U в ряд Тейлора |
относительно точки равновесия |
и сравнивая результат с |
||
предыдущим выражением, можно убедиться, что гармоническая силовая постоянная связи простым образом связана с энергией диссоциации связи:
k |
AB |
= 2α 2 |
D . |
(12) |
|
AB |
AB |
|
Потенциал Uсв при малых смещениях атомов от равновесного положения, равных ± 0,1 Å, является хорошим приближением для описания растяжения или сжатия связей. Если один из атомов поместить в начало координат, то r0 совпадает с межъядерным расстоянием; обычно эту величину называют длиной связи.
2.2.2. Потенциальная энергия деформации валентных и торсионных углов
Для описания деформации валентных углов можно также использовать разложение в ряд Тейлора. Если ограничиться квадратичным членом, то
U угл |
(θABC ) = |
1 |
kABC (θABC − θ0, ABC )2 , |
(13) |
|
||||
|
2 |
|
|
|
где kABC = 50 – 100 ккал/(моль·рад2) – деформационная силовая постоянная угла АВС, которую находят из колебательных спектров молекул. В большинстве случаев деформация валентных углов не превышает 3 – 5° и гармоническое приближение вполне удовлетворительно.
Торсионные углы описывают внутреннее вращение молекул вокруг связей, а потому являются периодическими функциями. Соответственно, потенциальная энергия является периодической функцией торсионных углов τ ABCD, и для каждого угла τ ABCD удобно представить в виде разложения в ряд Фурье (см. уравнение (2)):
U (τ ) = a0 + ∑amcosnmτ , |
(2a) |
m |
|
При n = 1 период вращения равен 360°, при n = 2 − 180°, при n = 3 − 120°, |
и т. д. |
2.2.3. Потенциальная энергия невалентных взаимодействий |
|
Потенциальная энергия Uневал может быть записана в виде суммы |
|
Uневал = Uэлектрост + UВдВ + UН-св + Uдоп, |
(14) |
где последовательно перечислены ее составляющие, связанные с электростатическим взаимодействием атомов, силами Ван-дер-Ваальса и отталкиванием на малых расстояниях, водородными связями, а также различные дополнительные взаимодействия, учитываемые в частных случаях. Рассмотрим все эти вклады более детально.
Распределение заряда в молекуле, состоящей из электронов и ядер, неоднородно. Проанализируем вначале постоянное электрическое поле, создаваемое молекулой, поместив центр масс двухатомной молекулы АВ с зарядами qA и qB, сосредоточенными на атомах в точках – zA и zB, в начало координат. Электростатический потенциал, создаваемый молекулой в некоторой точке P, равен
|
1 |
|
|
|
|
|
qB |
|
1 |
|
|
|
|
qA |
|
|
|
|
qB |
|
|
|
|
|||||||
|
|
|
qA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ϕ(r) = |
|
|
|
|
|
|
|
|
+ |
|
= |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
= |
||
|
4πε0 rA |
|
|
rB |
|
|
4πε |
0 |
(r 2 |
+ z2 |
+ 2rz |
A |
cosλ ) |
(r 2 + z2 |
− 2rz |
B |
cosλ ) |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
B |
|
|
|
|
||
= |
1 |
|
|
|
|
1 |
|
|
|
|
|
qA |
|
|
|
+ |
|
|
qB |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
(15) |
|||
|
4πε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 / 2 |
|
|
|
|
|
1 / 2 |
||||||
|
|
0 |
|
|
r |
(1 + [zA / r |
] + 2[zA / r]cosλ ) |
|
(1 + [zB/ r] |
− 2[zB/ r]cosλ ) |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||
где ε0 – электрическая постоянная. При zA << r |
и zB << r это выражение можно разложить в |
|||||||||||||||||||||||||||||
степенной ряд Тейлора по обратным расстояниям: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
12
|
1 |
|
q |
A |
+ q |
B |
|
|
q |
A |
z |
A |
− q |
B |
z |
B |
|
q |
A |
z2 |
+ q |
B |
z2 |
|
|
|
ϕ(r) ≈ |
|
|
|
|
|
|
− |
|
|
|
|
cosλ + |
|
A |
|
B |
(3cosλ − 1)+ K . |
(16) |
||||||||
4πε |
|
|
|
|
|
|
|
|
|
r 2 |
|
|
|
|
|
2r3 |
|
|
||||||||
|
0 |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Из этого выражения следует, что электростатический потенциал в точке Р, расстояние до которой больше, чем размер молекулы, может быть представлен в виде вкладов, связанных с электрическими моментами молекулы, или мультиполями (q = qА + qВ есть полный заряд молекулы)
μ = qA zi, A + qB zi, B , |
(17) |
Θij = qA zij2,A + qB zij2,B . |
(18) |
Данные величины называются дипольным и квадрупольным моментами молекулы соответственно. Электрические моменты – тензорные величины, поэтому они записаны через компоненты i, j.
Мультиполи можно определить для произвольного распределения заряда, как непрерывного, так и дискретного. В любом случае каждый из мультиполей можно эффективно представить определенным расположением зарядов: диполь представляется двумя зарядами разного знака, расположенными на некотором расстоянии друг от друга; квадруполь – четырьмя зарядами с попарно разными знаками, расположенными в вершинах квадрата; октуполь – четырьмя положительными и четырьмя отрицательными зарядами, расположенными в вершинах куба, и т.д. То, какие мультипольные моменты отличны от нуля, определяется симметрией системы.
Энергия электростатического взаимодействия пары двухатомных молекул рассчитывается как сумма произведений атомных зарядов на потенциал в точках их расположения. Результат дается формулой
|
U |
(q, q |
′ |
) = |
1 |
qq′ |
+ |
1 |
′ |
|
′ |
′ |
)+ |
μμ′ |
(2cosθcosθ |
′ |
′ |
|
|||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
4πε0 |
r 2 |
(qμ cosθ + q μcosθ |
r3 |
|
+ sinθsinθ cosζ )+ |
|
|||||||||||||
|
|
электрост |
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|||||
+ |
1 |
[qΘ′(3cos2 |
θ ′ − 1)+ q′Θ(3cos2 θ − 1)]+ |
3 |
[μΘ′{cosθ (3cos2 θ ′ − 1)+ 2sinθ sinθ ′cosθ ′cosζ }+ |
||||||||||||||||
2r3 |
2r 4 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
+ μ′Θ{cosθ ′(3cos2 θ − 1)+ 2sinθ ′sinθ cosθ cosζ }]+ |
3ΘΘ′ |
[1 − 5cos2θ − 5cos2 θ ′ + 17 cos2 θ cos2 |
θ ′ + |
||||||||||||||||||
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4r5 |
|
|
|
|
|
|||
|
|
|
|
+ 2sin2 θ sin2 θ ′cos2 ζ + 16sinθ sinθ ′cosθ cosθ ′cosζ ]+ K}. |
(19) |
||||||||||||||||
Вмультипольном приближении энергия Uэлектрост представляется в виде бесконечного ряда, включающего парные взаимодействия: заряд-заряд, заряд-диполь, диполь-диполь, заряд- квадруполь, диполь-квадруполь, квадруполь-квадруполь, и т.д. Все члены ряда зависят от различных степеней обратного расстояния между молекулами, причем показатель степени возрастает при увеличении ранга мультиполя. Основной вклад в энергию электростатического взаимодействия дает «монополь-монопольный» член, связанный с зарядами молекул. В
нейтральных молекулах эти заряды равны нулю, и основной вклад во взаимодействие дает диполь-дипольный член, пропорциональный r-3, величина которого уменьшается с ростом расстояния между молекулами значительно быстрее, чем в случае взаимодействия «заряд-заряд».
Вцелом, энергия взаимодействия двух мультиполей m и n уменьшается с ростом расстояния как r – ( n + m + 1).
Электростатический потенциал удобно представить в виде суммы вкладов, связанных с электрическими моментами атомов (атом-атомное приближение). Воспользуемся приближением парной аддитивности и ограничимся учетом наиболее значимого по величине взаимодействия «заряд-заряд». Тогда энергия электростатического взаимодействия описывается законом Кулона:
Uэлектрост |
(r) = |
qA qB |
(20) |
||
4πε |
0rAB |
||||
|
|
|
|||
Атомы в этом выражении полагаются точечными. Это наиболее часто применяемое приближение в механической модели молекулы.
Распределение электронной плотности в свободных атомах сферически симметрично, а, следовательно, все электрические моменты таких атомов равны нулю. В молекулах происходит перераспределение электронов по сравнению с совокупностью свободных атомов (такая система
13
называется промолекулой), поэтому атомные мультипольные моменты – характеристика связанных атомов.
Для более точного описания распределения неоднородного и анизотропного заряда в молекулах иногда применяется модель распределенных мультиполей: центры мультиполей помещают не только в положения атомов, но и на середины межъядерных векторов, а также в места наиболее вероятной локализации неподеленных электронных пар. Параметры модели распределенных мультиполей определяются подгонкой под электростатический потенциал, рассчитанный квантово-химическими методами. Метод имеет эмпирическую основу: универсального и единственного способа определить набор распределенных мультиполей не существует.
При взаимодействии полярных молекул необходимо учитывать эффект их взаимной поляризации. В атом-атомном приближении это достигается путем введения наведенных или индуцированных атомных диполей, величина которых определяется поляризуемостями атомов.
Энергия Ван-дер-Ваальса UВдВ (~ 0,1 – 0,2 ккал/моль) описывает неэлектростатическую часть невалентного взаимодействия между атомами и молекулами, которое имеет характер притяжения на расстояниях между частицами, превышающих 3 Å, и отталкивания, когда это расстояние меньше 2 Å. Природа обоих эффектов физически различна и состоит в следующем. При достаточно большом расстоянии между двумя нейтральными частицами мгновенная корреляция в движении электронов в этих частицах искажает распределение электронов в пространстве, что можно описать как появление у частиц мгновенных наведенных мультипольных моментов. Взаимодействие этих моментов называется дисперсионным, а возникающие силы – силами Лондона. По величине наиболее значимо диполь-дипольное взаимодействие; его среднее по ориентациям диполей значение зависит от расстояния между частицами как rAB−6 .
При бесконечном расстоянии между частицами энергия их взаимодействия равна нулю; при сближении частиц эта энергия достигает минимального (отрицательного) значения, а затем начинает возрастать, становясь положительной примерно при 2 Å. Это связано с тем, что по мере сближения частиц происходит обобществление принадлежащих им электронов, имеющее характер их интерференции (поскольку электрон обладает волновыми свойствами). Когда расстояние между частицами становится меньше равновесного, электронная плотность между ядрами уменьшается, и ядерное отталкивание более не компенсируется в полной мере электронным облаком. Кулоновский потенциал ядра с зарядом Z, частично экранированного электронами, имеет вид
ϕ(r) = |
1 |
|
Z |
exp(− ξr ), |
(21) |
4πε 0 |
|
||||
|
|
r |
|
||
где ξ − параметр экранирования, зависящий от расстояния до ядра r, то есть, от того, какая часть электронного облака эффективно уменьшает заряд ядра для рассматриваемого электрона. Поэтому можно ожидать, что потенциал отталкивания будет иметь экспоненциальный вид, причем он должен приближаться к нулю быстрее, чем r-6, так как энергия взаимодействия с ростом расстояния приближается к нулю со стороны отрицательных значений. К сожалению, использование экспоненциальной функции приводит к тому, что полный потенциал
U |
ВдВ |
(r |
) = − A r −6 |
+ B exp(−α |
r ) , |
(22) |
|
AB |
AB AB |
AB |
AB AB |
|
который в этом случае называется потенциалом Бэкингема – Хилла (потенциалом «6-exp»), при малых расстояниях становится отрицательным и даже стремится к – ∞ при r → 0. Кроме того, расчеты энергии молекул с экспоненциальными функциями требуют больших вычислительных затрат. Поэтому отталкивающая часть энергии Ван-дер-Ваальса чаще всего описывается эмпирическим членом, пропорциональным r-12; соответствующий потенциал, предложенный Леннард-Джонсом, имеет вид (потенциал «6-12»)
|
|
12 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
||
UВдВ (rAB ) = 4ε |
|
σ AB |
|
σ AB |
|
. |
(23) |
|
|
|
− |
|
|
|
|||
|
|
rAB |
|
rAB |
|
|
|
|
|
|
|
|
|
|
|
|
|
Параметр σ характеризует расстояние, при котором энергия взаимодействия Леннард-Джонса равна нулю (σ равно сумме вандерваальсовых атомных радиусов), а ε задает глубину
14
потенциальной ямы. Оба параметра зависят от пары взаимодействующих атомов и определяются из соображений воспроизводимости различных экспериментальных данных по свойствам реальных газов, жидкостей и твердых тел, а также в экспериментах по рассеянию атомов и молекул. Получаемые при этом потенциалы носят эффективный характер, так как включают в себя не только парные, но и игнорируемые моделью многоцентровые атомные взаимодействия, а также вклады в энергию, описываемые отброшенными индуцированными электрическими моментами высоких порядков. Параметры потенциала могут быть также рассчитаны методами квантовой химии.
Энергия слабых и промежуточных водородных связей X−H…Y UН-св, величина которой составляет обычно 1 – 5 ккал/моль на связь, имеет как электростатическую, так и дисперсионную компоненты. Расстояние H…Y существенно короче невалентного контакта, а потенциал водородной связи более глубокий. Наиболее часто для описания водородных связей применяется потенциал вида
U |
Н −св |
(r |
) = |
AHY |
− |
CHY |
, |
(24) |
r12 |
|
|||||||
|
HY |
|
|
r10 |
|
|||
|
|
|
|
HY |
|
HY |
|
|
в котором АHY и СHY являются эмпирическими параметрами. Для точного описания энергетики водородной связи вносят поправки, учитывающие геометрию водородной связи (рис. 8):
|
|
UН −св (rHY ) = |
C |
HY |
− |
D |
|
|
m |
|
|
|||
|
|
|
|
|
HY |
|
|
|
||||||
X |
θ |
|
rHY6 |
rHY4 |
cos |
θ , |
|
(25) |
||||||
|
|
UН−св (rHY ) = |
|
A |
− |
C |
|
|
2 |
4 |
|
|||
H |
|
|
HY |
|
HY |
(26) |
||||||||
|
|
12 |
10 |
cos |
θcos ω . |
|||||||||
ω |
Y |
|
|
rHY |
|
rHY |
|
|
|
|
|
|||
Cильные водородные связи, энергия которых достигает 60 |
||||||||||||||
|
|
|||||||||||||
Рис. 8. Геометрия водородной связи. |
ккал/моль, |
|
требуют |
|
учета |
валентной |
составляющей |
|||||||
|
|
взаимодействия H…Y. |
|
|
|
|
|
|||||||
Следует отметить, что парные потенциалы Леннард-Джонса не полностью описывают дисперсионные взаимодействия. Кроме того, все взаимодействия в системе взаимно связаны и влияют друг на друга. В отдельных случаях все эти факторы приходится учитывать, для чего вводится дополнительный член Uдоп, имеющий эмпирическую природу; конкретный вид Uдоп зависит от специфики решаемой задачи.
Приведенные уравнения и входящие в них параметры определяют силы, действующие в молекулах. Поэтому механическую модель молекулы часто называют моделью силового поля. Параметры силовых полей подгоняют таким образом, чтобы они были применимы к как можно более широкому кругу соединений, то есть, чтобы они были переносимыми от одной системы к другой. К сожалению, такая переносимость оправдана лишь в рядах сходных соединения; разные задачи и разные системы требуют разных характеристик. Поэтому существует множество силовых полей, полный анализ и область применимости которых можно найти в литературе.
Приведенные выражения связывают минимальную энергию молекулы с равновесными значениям длин связей, валентных и торсионных углов и невалентных контактов. Это означает, что для каждой пары атомов одного или разного сорта, а также для троек и четверок различных атомов должны быть определены «идеальные» равновесные значения межатомных расстояний и валентных и торсионных углов. Отклонения этих величин от идеальных значений («напряжения» структуры молекулы) требуют затрат энергии. Поиск стабильных конформаций, отвечающих локальным минимумам ППЭ, в рамках механической модели молекулы основан на минимизации энергии этого напряжения. Это достигается путем изменения координат атомов. Энергетически неблагоприятные взаимодействия, повышающие энергию молекулы, называются стерическими эффектами.
Рассмотренная модель не дает абсолютных значений энергий напряжения молекул, т.к. отсчитывать их приходится от разных начальных уровней. Поэтому физический смысл имеют лишь относительные энергии различных конформаций и сравнивать энергии даже близких по строению молекул нельзя. Это ограничивает применимость механической модели молекулы
15
кругом задач, связанных с конформационным анализом. При этом силовые поля можно разделить на две группы. Первая из них, так называемые силовые поля класса I, приспособлена для изучения структуры больших биомолекул: используемые аппроксимации для компонент потенциальной энергии здесь максимально упрощены. Вторая группа, образующая силовые поля класса II, ориентирована на исследование геометрии и колебательных характеристик малых и среднеразмерных молекул: формулы, описывающие энергию в этой группе, используются с меньшим числом приближений и учитывают довольно много факторов, влияющих на структуру. Предложено множество различных вариантов силовых полей, параметры которых ориентированы на исследование специфических молекулярных систем.
2.3. Ограничения механической модели
Точность описания структуры в рамках механической модели молекулы может быть оценена сравнением с экспериментальными данными, полученными, например, с помощью электронографии молекул в газовой фазе, или с данными неэмпирических квантово-химических расчетов высокого уровня. Для малых молекул при хорошо подобранных параметрах потенциалов ошибки воспроизведения длин связей обычно составляют ~ 0,01 Å, валентных углов ~ 1° , частот колебаний ~ 102 ГГц или 3,3 см-1 (то есть, ~ 10 %), барьеров внутреннего вращения ~ 0,4 ккал/моль.
Основные источники погрешности силовых полей связаны с неполным или некорректным учетом неаддитивных и трехчастичных взаимодействий и эффектов поляризации атомов, использованием комбинационных правил для описания неизвестных параметров и ограниченностью монопольной аппроксимации электростатических взаимодействий. Каждый из этих факторов может вносить погрешности до 10 % , а их одновременное действие может исказить результат существенным образом.
Существуют, однако, более глубокие причины, ограничивающие применимость классической механики в теории строения молекул. Среди принципиальных причин, прежде всего, следует упомянуть теорему Ирншоу, утверждающую, что устойчивое равновесие системы неподвижных зарядов, взаимодействующих по закону обратных квадратов, невозможно. Следовательно, учет электростатического взаимодействия по закону Кулона в молекуле, представляемой в виде набора точечных атомов с нулевой кинетической энергией, в рамках классической механики не может обеспечить ее устойчивости. Кроме того, в силу квантово- механического принципа неопределенности, атомным ядрам нельзя приписать строго определенных положений в пространстве. Даже при нулевой температуре по Кельвину ядра совершают нулевые колебания; следовательно, они распределены в пространстве вокруг точек равновесия и имеет смысл говорить лишь об их средних значениях.
16

3. КВАНТОВО-МЕХАНИЧЕСКИЕ ПРИНЦИПЫ ОПИСАНИЯ МОЛЕКУЛЯРНЫХ СИСТЕМ
В начале XX в. было экспериментально установлено, что для частиц атомно-молекулярных размеров наряду с корпускулярными свойствами характерно также наличие волновых свойств. Этот дуализм (двойственность) свойств микрочастиц создавал трудности в описании их поведения с помощью понятий классической механики. Созданная квантовая механика стала физической основой теории строения и свойств атомов и молекул.
Дуализм свойств микрочастиц выражается соотношением де Бройля:
λ = |
h |
, |
(27) |
|
|||
|
p |
|
|
где λ – длина волны; h – постоянная Планка; p = mv – импульс частицы. Хотя дуализм – общее свойство материи, ожидать его проявления можно только для микрообъектов.
Волновые свойства микрочастиц приводят к ограниченному применению к ним некоторых понятий, которыми характеризуется частица в классической механике. Если для макрочастицы в классической механике принципиально возможно одновременно точно определить и координату (x, y, z) и составляющие вектора импульса относительно координат (px, py, pz), то для микрочастицы в квантовой механике это невозможно. Для микрочастиц всегда имеется неопределенность в координате x ( y, z) или импульсе px ( py, pz) а также для таких динамических переменных, как время и энергия. Принцип неопределенности, открытый Гейзенбергом, математически выражается следующими соотношениями:
|
x |
px ≥ |
H |
, |
|
(28) |
||
|
|
|
|
|||||
|
|
2 |
|
|
|
|||
|
t |
E ≥ |
H |
, |
|
(29) |
||
|
|
|
||||||
|
|
2 |
|
|
|
|
||
где x и px, |
t и E – неопределенности |
координаты и |
импульса, времени и |
энергии |
||||
соответственно; ħ = h/2π – постоянная Дирака. |
|
|
|
|
|
|
|
|
Принцип |
неопределенности показывает, |
что движение |
микрочастицы нельзя |
описать |
||||
определенной траекторией. Можно лишь говорить о вероятности нахождения микрочастицы в данном элементарном объеме.
3.1. Постулаты квантовой механики
Вся квантовая механика строится на нескольких основных постулатах.
1.О волновой функции. Любое состояние системы полностью описывается некоторой функцией Ψ(q1, q2, …, qn, t) от координат всех образующих систему частиц и времени, называемой функцией состояния системы или ее волновой функцией. Волновая функция не имеет аналога в классической физике и сама по себе не имеет физического смысла.
2.О способе описания физических величин. Каждой динамической переменной
(координата, импульс, энергия и т.д.) в классической физике ставится в соответствие линейный самосопряженный оператор в квантовой механике. Все функциональные отношения между
величинами классической механики в квантовой механике заменяются отношениями между операторами * . В квантовой механике вид оператора постулируется. Операторы некоторых физических величин (A → Â) представлены в табл. 1.
Операторы должны удовлетворять условию
(xˆpˆx − pˆx xˆ)Ψ = iHΨ , |
(30) |
т.е. коммутатор от xˆ и pˆ должен быть равен iħΨ. В соответствии с принципом неопределенности, невозможно определить одновременно переменные из этих двух групп с заданной точностью. Соотношение (30) является другой математической формой принципа неопределенности.
* Сведения об операторах приведены в Приложении А.

Таблица 1. Операторы некоторых физических величин
Физическая величина |
|
|
|
|
|
|
|
|
|
|
Оператор |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Координата x → xˆ |
x |
|
|
|
|
|
|
|
|
|
|
|
|
Функция от координаты f (x) → fˆ(x) |
f(x) |
|
|
|
|
|
|
|
|
||||
Составляющая импульса Px → pˆx |
|
|
∂ |
|
|
|
|
|
|
|
|||
iH |
|
|
(i = |
− 1 – мнимая единица) |
|||||||||
|
|
||||||||||||
|
|
|
∂x |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
∂ |
|
|
∂ |
|
∂ |
|
||
Вектор импульса P → pˆ |
− iH i |
+ j |
|
+ k |
≡ −iH |
||||||||
|
|
|
|
||||||||||
|
|
|
|
|
∂x |
|
∂y |
|
|
|
|||
|
|
|
|
|
|
|
∂z |
||||||
ˆ |
f ( p) |
|
|
|
|
|
|
|
|
||||
Функция от вектора импульса f ( p) → f ( p) |
|
|
|
|
|
|
|
|
|||||
|
|
ˆ |
|
|
|
|
|
|
|
|
|||
Оператор кинетической энергии Tˆ |
− |
|
H2 |
2 (m – масса частицы) |
|||||||||
2m |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значения физических величин, определяемые по собственным значениям операторов этих величин, должны быть всегда действительными, т.е. не содержащими мнимой части. Эрмитовы операторы обладают замечательным свойством: их собственные значения всегда действительны. Поэтому операторы физических величин квантовой механики представляют собой линейные самосопряженные операторы, по собственным значениям которых с помощью волновой функции возможно полное описание квантовой системы.
3. Об основном уравнении квантовой механики. Волновая функция должна удовлетворять уравнению
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
|
iH |
Ψ(R,t) = − |
|
|
|
|
|
|
|
|
|
∂t |
||
|
|
|
|
|
|
|
|
|
|
|
где |
2 |
= |
∂2 |
+ |
∂2 |
+ |
∂2 |
– оператор Лапласа; R |
||
|
∂x2 |
∂y2 |
∂z2 |
|||||||
|
|
|
|
|
|
|
|
|||
H |
2 |
|
2 |
ˆ |
|
Ψ(R,t) , |
(31) |
|
|
|
|||||
|
|
|
+ U |
||||
2m |
|
|
|
|
|
||
– радиус-вектор, определяющий координаты;Uˆ –
оператор потенциальной энергии. Величина, стоящая в уравнении (31) в квадратных скобках, называется оператором Гамильтона или гамильтонианом и обозначается символом Hˆ . Как видно, оператор Гамильтона есть сумма операторов кинетической и потенциальной энергий.
Это уравнение не может быть выведено, оно постулировано Шрёдингером и известно как волновое уравнение Шрёдингера (см. Приложение B). Наличие мнимой единицы в волновом уравнении приводит к тому, что уравнение Шрёдингера представляет собой пару уравнений с комплексно сопряженными волновыми функциями Ψ и Ψ*.
В обычных задачах структурной химии и молекулярной физики, при интерпретации реакционной способности и физических свойств молекул важны только так называемые стационарные состояния системы, т.е. состояния, не зависящие от времени. При их описании считается, что гамильтониан явно не зависит от времени. Тогда в приведенном уравнении (31) можно разделить переменные, представив волновую функцию Ψ(R,t) в виде произведения координатной Ψ(R) и временной Φ(t) частей:
Ψ(R,t) = Ψ(R) Φ(t) , |
(32) |
|||||
ˆ |
∂Φ(t) |
|
1 |
|
|
|
HΨ(R) |
= iH |
|
. |
(33) |
||
|
∂t |
|
||||
Ψ(R) |
|
Φ(t) |
|
|||
Нетрудно заметить, что уравнение Шрёдингера (31) сводится к двум независимым уравнениям, связанным между собой лишь константой E, которая является собственным значением оператора Гамильтона, т.е. полной энергией квантовой системы:
ˆ |
= EΨ(R) , |
(34) |
||
HΨ(R) |
||||
iH |
∂Φ(t) |
= EΦ(t) . |
(35) |
|
∂t |
||||
|
|
|
||
2

Уравнение (34) является линейным дифференциальным уравнением второго порядка и называется
стационарным уравнением Шрёдингера. Второе уравнение имеет решение
|
iEt |
|
|
Φ(t)= Φ0exp − |
|
. |
(36) |
|
|||
|
H |
|
|
Стационарное уравнение Шрёдингера (34) определяет волновую функцию лишь с точностью до произвольного постоянного множителя C; этот множитель находится из так называемого
условия нормировки
C∫ ΨΨ*dV = C∫ |
|
Ψ |
|
2 dV = 1, |
(37) |
|
|
||||
|
|
|
где dV – элемент объема в пространстве, определяемом всеми переменными. Квадрат модуля волновой функции Ψ2 пропорционален вероятности нахождения микрочастицы в единице
объема и называется плотностью вероятности. Поэтому условие нормировки (37) означает, что вероятность нахождения частицы во всем пространстве равна единице. Волновые функции должны быть конечными, непрерывными, однозначными и обращаться в нуль там, где частица находиться не может.
Функции Ψi и Ψj, относящиеся к различным собственным значениям Ei и Ej, ортогональны, т.е. выполняются соотношения:
∫ ΨiΨjdV = 0 , |
i ≠ j . |
(38) |
|
Условие одновременной ортогональности и нормированности (ортонормированности) |
|||
функций Ψi (i = 1, 2, …, ∞) записывается следующим образом: |
|
||
∫ ΨiΨjdV = δij , |
(39) |
||
где δij – дельта-символ Кронекера, имеющий вид: |
|
|
|
0, |
если |
i ≠ j, |
|
δij = |
|
i = j. |
(40) |
1, |
если |
|
|
В силу перечисленных условий в стационарном уравнении Шрёдингера гамильтониан – линейный самосопряженный оператор – всегда имеет полную систему собственных функций Ψi(R), каждой из которых соответствует собственное значение Ei. Таким образом, энергия принимает ряд дискретных допустимых значений (квантование энергии). Если одно собственное значение соответствует нескольким (m) собственным функциям, то данное состояние называется вырожденным с кратностью вырождения, равной m. (Можно привести пример: 3p-орбитали атома азота имеют одну и ту же энергию, т.е. кратность вырождения данного состояния равна 3.)
4. О возможных значениях физических величин. Единственно возможными значениями,
которые могут быть получены при измерении динамической переменной A, являются собственные значения Â операторного уравнения
ˆ |
= AΨi . |
(41) |
AΨi |
5. О среднем значении физической величины. Среднее значение физической величины A ,
имеющей квантовомеханический оператор Â, в состоянии Ψ определяется соотношением
|
|
|
|
|
|
|
* |
ˆ |
|
|
|
|
A = ∫ Ψ |
|
(42) |
||||||||
|
|
AΨdV . |
|||||||||
Например, среднее значение полной энергии системы в состоянии Ψ равно |
|
||||||||||
|
|
* |
ˆ |
|
(43) |
||||||
|
|
||||||||||
E = ∫ Ψ |
HΨdV . |
||||||||||
При выполнении условия ортонормированности |
|
|
|
|
|||||||
|
|
|
|
|
|
|
∞ |
|
|
2 Ai . |
|
|
|
|
|
|
|
= ∑ |
ci |
|
|||
|
|
|
|
A |
(44) |
||||||
|
|
|
|
|
|
i=1 |
|
|
|
||
Для коэффициентов ci выполняется соотношение |
|
|
|
||||||||
|
|
|
|
|
|
∞ |
|
|
2 = 1, |
|
|
|
|
|
|
|
|
∑ |
ci |
(45) |
|||
i=1
означающее условие нормированности Ψ при разложении по ортонормированному базисному набору. Это позволяет интерпретировать |ci|2 как вероятность того, что в результате отдельного
3

измерения наблюдаемой величины A будет получено значение Ai, отвечающее собственной функции Ψi.
6. Принцип суперпозиции состояний. Этот принцип вытекает из свойства линейности оператора. Если система может находиться в состояниях, описываемых волновыми функциями Ψ1 и Ψ2, то она может находиться и в состоянии
Ψ = C1Ψ1 + C2Ψ2 , |
(46) |
где С1 и С2 – произвольные константы, которые при условии ортонормированности Ψ1 и Ψ2 находят из соотношения (37). Из принципа суперпозиции следует, что функция Ψ описывает такое состояние, при котором система находится либо в состоянии Ψ1 с вероятностью, равной C12 , либо
всостоянии Ψ2 с вероятностью C22 .
7.Об антисимметричности волновой функции. Волновая функция системы частиц с полуцелым спином (в частности, электронов) должна быть антисимметрична относительно перестановки координат любых двух частиц. Для двух частиц это свойство волновой функции выглядит как
Ψ(q1,q2 )= −Ψ(q2 ,q1 ), |
(47) |
а для системы n частиц |
|
Ψ(q1,q2 ,K,qi ,K,qj ,K,qn )= −Ψ(q1,q2 ,K,qj ,K,qi ,K,qn ). |
(48) |
Для системы с антисимметричными волновыми функциями справедлив принцип запрета Паули: в одном и том же одночастичном состоянии не может быть даже двух электронов, одночастичные состояния которых определяются значениями четырех квантовых чисел.
3.2. Основные приближения при решении волнового уравнения
Для описания поведения какой-либо микрочастицы, например, электрона, необходимо решить уравнение Шрёдингера, т.е. найти выражение для волновой функции Ψ как функции всех координат и энергию данной микрочастицы.
Точное решение уравнения Шрёдингера удается получить только для системы, состоящей из двух частиц (например, в Приложении C приведено решение уравнения Шрёдингера для атома водорода). Математические трудности не позволяют решить эту задачу для более сложных атомных и молекулярных систем. Поэтому приходится вводить различные приближения, которые можно разделить на две группы. Первая включает приближения, которые упрощают выражение для оператора энергии (гамильтониана) и имеют, как правило, общий характер, так что их можно использовать в ряде различных методов. Ко второй группе относятся приближения, которые касаются определения значений интегралов, появляющихся в различных вычислительных схемах. Приближения такого типа специфичны для каждого конкретного вычислительного метода. Рассмотрим три приближения из первой группы*.
3.2.1. Пренебрежение неэлектростатическими взаимодействиями
Полный гамильтониан системы Hˆ можно представить в виде суммы трех операторов:
ˆ ˆ |
ˆ |
ˆ |
, |
(49) |
H = Hэ.я |
+ Hвнешн |
+ Hвнутр |
где Hˆ э.я – оператор кинетической энергии и электростатического взаимодействия всех входящих в систему электронов и ядер; Hˆ внешн – оператор взаимодействия системы с внешними магнитными и электрическими полями; Hˆ внутр – оператор неэлектрических взаимодействий между частицами
данной системы, которые связаны с наличием спинового движения электронов и ядер. В случае пренебрежения неэлектростатическими взаимодействиями и влиянием внешних полей полный гамильтониан Hˆ ≈ Hˆ э.я . Это пренебрежение используется почти во всех методах квантовой химии.
* Одним из широко используемых методов решения уравнения Шрёдингера является вариационный принцип, подробно рассмотренный в Приложении D.
4
