кванты лекции

3.2.2. Адиабатическое приближение Борна – Оппенгеймера

Поскольку массы ядер много больше массы электронов (в 103 – 105 раз), скорости движения ядер во много раз меньше скоростей электронов, что позволяет рассматривать движение электронов отдельно от движения ядер. Ядра при решении электронной задачи считаются фиксированными, расположенными на заданных расстояниях друг от друга. В квантовой механике это эквивалентно допущению, что полная волновая функция молекулы Ψ (R, R) (R и R – радиус- векторы, задающие координаты электронов и ядер соответственно) может быть представлена как произведение двух отдельных волновых функций

где ψe – электронная волновая функция, связанная с распределением электронной плотности, а ψn – ядерная волновая функция. Приближение (50) называется адиабатическим, т.к. вследствие большого различия в скоростях движения, электроны адиабатически (без градиента энергии) следуют за движением ядер.

Волновое уравнение в приближении Борна – Оппенгеймера будет иметь вид:

где Ee – электронная энергия, определяемая движением n электронов в поле N ядер, плюс энергия взаимодействия между ядрами. Энергия Ee представляет адиабатический электронный терм молекулы или адиабатический потенциал и определяется как собственные значения оператора Hˆe .

При решении уравнения (51) для каждой волновой функции ψe(R, R) и для каждого определяемого этой функцией электронного состояния параметр R рассматривается как фиксированный.

В ходе химической реакции меняется взаимное расположение ядер. Это означает, что для того, чтобы проследить путь химической реакции, необходимо многократно решить электронное волновое уравнение для всех возможных координат R. Электронная энергия в этом случае представляет собой потенциальную энергию при изучении движения ядер, а ее зависимость от ядерных координат будет ППЭ (см. раздел 5.2).

3.2.3. Одноэлектронное приближение Хартри – Фока (модель независимых электронов)

Гамильтониан n-электронной системы имеет вид:

Идея приближения заключается в том, что влияние всех электронов на движение каждого выделенного электрона заменяется действием некоторого эффективного поля. При этом движение электрона определяется лишь его координатами в потенциальном поле, создаваемом ядерными зарядами и эффективным полем остальных электронов. Движения электронов разделяют, т.е. предполагают, что каждый электрон в системе движется независимо от всех остальных. Это позволяет представить Ψ как произведение одноэлектронных волновых функций:

Здесь подстрочные числа соответствуют номеру электронного состояния, а числа в скобках – формальному номеру электрона, имеющего координаты Ri.

Однако функция в виде (53) не может быть волновой функцией, т.к. она не обладает свойством антисимметрии к перестановкам электронов, т.е. не удовлетворяет принципу Паули (раздел 3.1, постулат 7). Действительно, для системы двух электронов выражение (53) можно записать в виде

Ψ′ = ψ1(1)ψ 2 (2) .

Операция перестановки электронов приводит к новой функции, отличной от предыдущей:

Ψ′′ = ψ1(2)ψ 2 (1) .

Для того чтобы Ψ была антисимметрична, необходимо ее представить в виде линейной комбинации (т.е. детерминаната):

5

Кроме того, необходимо учесть наличие у электрона спина, который может быть равен ±1/2. Для этого рассматривается волновая функция ψ(R, s), которая зависит от координат электрона и спина и называется спин-орбиталью. Поскольку пространственные и спиновые движения электронов происходят независимо друг от друга, то

где ψ(s) – спиновая волновая функция, которая обозначается α, если s = 1/2, и β, если s = –1/2. Спин-орбитали ортонормированны, если ортонормированны соответствующие функции ψ(R).

Таким образом, волновую функцию для системы из n электронов, можно представить в виде детерминанта n-го порядка, включающего независимые ортонормированные спин-орбитали отдельных электронов:

Этот определитель (детерминант) называется определителем Слэтера. Перестановке двух электронов соответствует перестановка двух столбцов определителя, что приводит к смене его знака. Детерминант равен нулю, если две строки будут одинаковыми. Физический смысл детерминанта Слэтера состоит в том, что в нем происходит смешение всех электронов данной системы по всем возможным орбиталям, в итоге удовлетворяется одно из основных положений квантовой механики о том, что положение электрона определяется плотностью вероятности.

Действуя гамильтонианом вида (52) на волновую функцию, представленную в виде детерминанта Слэтера (56), получим выражение для полной энергии:

где суммирование по i и j проводится по n/2 пространственным атомным орбиталям, причем каждая орбиталь заполнена двумя электронами. В уравнении (57)

называется остовным интегралом и представляет собой сумму кинетической энергии электрона 1 на орбитали ψi и потенциальной энергии притяжения его к ядру.

Двухэлектронный интеграл

называется кулоновским и характеризует среднюю энергию электростатического отталкивания электронов 1 и 2, находящихся на орбиталях ψi и ψj. Jˆ j (1) – кулоновский оператор.

Интеграл

называется обменным. Kˆ j (1) – обменный оператор. В одноэлектронном приближении обменный

интеграл лишь частично учитывает электронную корреляцию, вызванную взаимодействиями между электронами. Сумма кулоновского и обменного интегралов в уравнении (57) определяет взаимодействие рассматриваемого электрона 1 с усредненным полем остальных электронов.

Следующий шаг – минимизация энергии в (57) с помощью вариационного принципа (см. Приложение D) при условии, что атомные орбитали остаются ортонормированными. Выполнение этого условия обеспечивается множителями Лагранжа εji, имеющими размерность энергии. Составляется функционал

6

j

является оператором Хартри – Фока, или фокианом. Фокиан – оператор Гамильтона для одного электрона, находящегося в эффективном поле ядра и остальных электронов.

Решают уравнение Хартри – Фока итерационным путем. Выбирают на основе каких-либо соображений начальные функции ψ i0 , с ними определяют кулоновский Jˆ0j и обменный Kˆ 0j члены,

необходимые для вычисления фокиана. После подстановки в уравнение Хартри – Фока находят новый набор волновых функций ψ i1 , с помощью которого снова рассчитывают фокиан. Процесс

повторяется до тех пор, пока на каком-либо этапе не получатся одни и те же волновые функции (т.е. итерации сходятся). Решение уравнений на конечном шаге итераций является «согласованным с полем потенциала», которое определяется кулоновскими и обменными операторами. Такое поле получило название самосогласованного, а сам метод Хартри – Фока –

метода самосогласованного поля (ССП).

Численное решение уравнений Хартри – Фока приводит к достаточно точному решению и хорошему воспроизведению свойств многоэлектронных атомов.

Полная энергия электрона, находящегося на орбитали ψi (одна из орбиталей окончательного набора), равна

Полная энергия многоэлектронной системы равна сумме полных энергий всех электронов за вычетом энергии межэлектронного отталкивания:

Если при отрыве электрона с орбитали ψi не происходит изменения волновых функций ψj (j ≠ i), то εi можно приравнять (с противоположным знаком) к потенциалу ионизации i-ой орбитали Ii:

Этот результат известен под названием теоремы Купманса. Во многих случаях потенциалы ионизации, вычисленные с помощью теоремы Купманса, оказываются хорошим приближением к истинным потенциалам ионизации и поэтому из-за простоты вычислений используются как оценки.

3.3. Теория химической связи и квантово-химический расчет молекул

Для приближенного представления вида волновой функции основного состояния системы электронов молекулы существует два метода: метод валентных связей (ВС) и метод молекулярных орбиталей (МО). Оба метода подходят к построению исходной волновой функции

7

совершенно различными путями, а потому отражают разные представления об основном строении молекулы. Однако в высших своих приближениях они приводят к практически одинаковым результатам. Для расчета многоатомных систем в настоящее время предпочтение отдается методу МО, поскольку метод ВС является более трудоемким.

3.3.1. Метод валентных связей

В данном методе полагают, что при образовании молекулы из атомов последние в значительной степени сохраняют свою электронную конфигурацию, а силы связывания между атомами обусловлены обменом электронами между ними в результате спаривания спинов двух электронов, принадлежащих разным атомам. Это означает, что молекулярную волновую функцию необходимо строить из волновых функций отдельных атомов.

Рассмотрим простейший случай – молекулу водорода. Гайтлер и Лондон впервые рассчитали молекулу водорода с использованием разработанного ими метода ВС. В основном состоянии для двух невзаимодействующих атомов водорода a и b волновую функцию, зависящую от координат электронов, можно записать в виде

где ψa и ψb – волновые функции атомов водорода (атомные орбитали, АО) a и b. Аналитический вид волновых функций атомов водорода известен (см. Приложение C). Ввиду неразличимости электронов эквивалентной является и другая форма записи:

является интегралом перекрывания волновых функций ψa и ψb; J – кулоновский интеграл, вклад в энергию связи, обусловленный электростатическими взаимодействиями неискаженных электронных облаков атомов между собой и с ядром соседнего атома, определяется по аналогии с (59); K – обменный интеграл, вклад, обусловленный деформацией электронного облака при образовании связи и перемещением его в пространство между ядрами, определяется аналогично (60); EH – энергия изолированных атомов водорода.

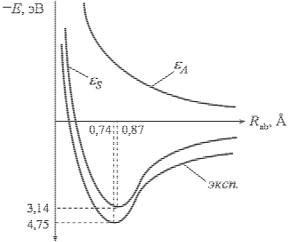
Все интегралы рассчитываются в адиабатическом приближении, т.е. при закрепленных на расстояниях Rab ядрах. Меняя межъядерное расстояние и решая для каждого Rab задачу заново, получают зависимость εS и εA от Rab (рис. 9). Как видно из рис. 9, молекула водорода в энергетическом состоянии εS отвечает устойчивому состоянию системы с минимумом энергии. Состояние молекулы

8

водорода, имеющее энергию εA, отвечает отталкиванию атомов; молекула водорода в этом энергетическом состоянии существовать не может.

Основному и возбужденному состояниям молекулы соответствуют волновые функции:

Для учета спинового состояния электронов необходимо пространственные волновые функции ΨS и ΨA умножить на спиновые функции, причем такой симметрии, чтобы это произведение было антисимметрично по отношению к перестановке координат электронов (принцип Паули). Для основного состояния молекулы водорода

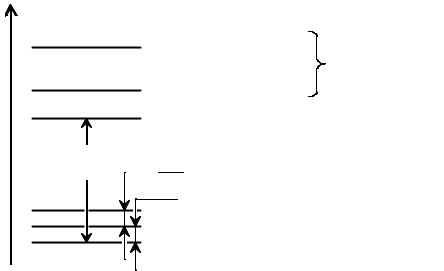
Единственное состояние, описываемое волновой функцией (77), называется синглетным. В синглетном состоянии суммарный спин электронов равен нулю. Возбужденное состояние молекулы водорода может осуществляться в нескольких вариантах:

Состояние молекулы водорода в этом случае описывается тремя волновыми функциями, которые отвечают одной энергии:

Такое трижды вырожденное состояние молекулы водорода называется триплетным. Триплетное состояние не может возникнуть из основного при поглощении кванта света, поскольку переходы с изменением мультиплетности запрещены правилами отбора так же, как и в случае атома. Однако такое состояние может возникнуть термическим путем, т.е. возбуждением при столкновении.

Отталкивательное триплетное состояние молекулы водорода возникает из основного состояния двух атомов водорода. Согласно квантовой статистике вероятность состояния пропорциональна его мультиплетности. Синглетное состояние реализуется одним способом (суммарный спин равен нулю), а триплетное – тремя (проекция суммарного спина может принимать значения 1, 0, –1). Поэтому при встрече двух атомов состояние отталкивания реализуется с вероятностью 75 %.

3.3.2. Метод молекулярных орбиталей

В этом методе полная волновая функция молекулы строится из волновых функций, описывающих поведение отдельных электронов в поле, создаваемом остальными электронами и всеми атомными ядрами, которые образуют молекулярный остов. Тем самым, концепция МО близка к концепции АО* с той лишь разницей, что МО являются многоцентровыми орбиталями.

* Атомная орбиталь – одноэлектронная волновая функция, полученная решением уравнения Шрёдингера для данного атома, задается главным n, орбитальным l и магнитным m квантовыми числами (см. Приложение С).

9

Несомненным удобством этой концепции является возможность перенесения математического аппарата, развитого для АО, на МО.

Молекулярной орбитали присущи все фундаментальные принципы и свойства атомных орбиталей, в том числе принцип Паули. Подобно атомным орбиталям, МО представляет собой одноэлектронную функцию, включающую пространственную и спиновую компоненты – спин- орбиталь. Каждая спин-орбиталь характеризуется своим значением энергии, определяющим последовательность заполнения МО в молекуле. Полная волновая функция молекулы, содержащей 2n электронов на n МО, записывается в виде детерминанта Слэтера, учитывающим требование антисимметрии волновой функции по отношению к перестановке любой пары электронов.

Существуют различные варианты составления МО. Наиболее наглядным, информативным и удобным оказался метод, в котором МО записывается как линейная комбинация всех АО (МО ЛКАО):

ν =1

где Ψi – МО для i-го электрона; ψν(i) – атомная волновая функция i-го электрона, принадлежащего ν-му атому; сiν – коэффициенты разложения МО; N – количество атомов, составляющих молекулу.

Совокупность МО молекулы, занятых электронами, называют ее электронной конфигурацией. Электронная конфигурация молекулы так же, как и атома, строится на основе двух фундаментальных положений – принципа наименьшей энергии (электрон занимает в молекуле свободную орбиталь с наименьшей энергией) и принципа Паули (на одной МО не может находиться более двух электронов, при этом спины электронов должны быть антипараллельны).

Используем приближение ЛКАО в рамках метода ССП (такой метод называется МО ЛКАО ССП). При подстановке уравнения (79) в функционал

и отыскании минимума энергии относительно ciν получается нелинейная алгебраическая система уравнений, коэффициенты в которой имеют вид кулоновских интегралов (59) с функциями ψν(i).

Эту систему называют уравнениями Хартри – Фока – Рутаана:

где εi – одноэлектронная энергия орбитали Ψi; индекс N относится к ядру, которому принадлежит µ-ый электрон; Sµν – элемент матрицы размерности N×N, называемой матрицей интегралов перекрывания (по ее элементам можно судить о степени пространственного перекрывания АО)

В этом выражении Hµν является матричным представлением энергии электрона в поле «голых» ядер

величина µν λσ представляет собой двухэлектронный интеграл отталкивания:

10

Суммирование ведется по всем занятым электронами МО. Коэффициент 2 отражает, что каждую орбиталь занимают два электрона.

Уравнения Хартри – Фока – Рутаана (81) лежат в основе почти всех современных неэмпирических (ab initio) методов расчета сложных молекулярных систем * . Эти уравнения решают с помощью процедуры самосогласования, которая состоит в следующем.

1. Сначала задаются начальными коэффициентами ci(0)ν , с помощью которых вычисляют начальное приближение матрицы Фока Fµν(0) . Считая на этом этапе, что она не зависит от искомых коэффициентов разложения, получают систему однородных линейных уравнений:

N

∑(Fµν(0) − εiSµν )ciν = 0 , µ = 1, 2, …, N.

ν=1

2.Решается полученная система уравнений, которая имеет ненулевые решения, если ее

детерминант равен нулю:

Fµν(0) − ε iSµν = 0.

Отсюда находят набор корней εi(0) .

3.Подставляя полученный набор корней в уравнение (81), находят ci(1)ν .

4.С помощью этих коэффициентов снова рассчитывают элементы матрицы Фока, затем εi(1) .

Таким образом, проводят цикл вычислений

…→ci(k)ν → Fµν(k) → εi(k) →ci(kν +1) → Fµν(k+1) → ε i(k+1) →…

до тех пор, пока полная энергия и матрица порядков связей для двух последовательных вычислений (итераций) не будут совпадать с заданной точностью.

Из выражения (79) следует, что свойства МО находятся в прямой зависимости от свойств образующих ее АО. Обсуждая метод МО ЛКАО ССП, мы полагали, что АО, образующие МО, определены. На самом деле, аналитического выражения для АО многоэлектронных атомов не существует. Поэтому возникает проблема описания АО теми или иными функциональными зависимостями, обеспечивающими надежное приближение к точному виду АО.

Набор АО, используемых при квантово-химических расчетах молекул, называется атомным базисом. Чем больше набор базисных функций, тем более точные решения для МО могут быть получены. С этой точки зрения в наиболее точных расчетах стремятся к увеличению базиса. Однако, при размере базиса (т.е. числе базисных функций) N общее количество интегралов при решении уравнений Хартри – Фока – Рутаана составляет N4/8. Так, при N = 100 необходимо решить более десяти миллионов интегралов. В связи с этим, практическое решение уравнений Хартри – Фока – Рутаана на современных компьютерах сталкивается с двумя проблемами: необходимо наличие значительных компьютерных ресурсов, расчеты могут занимать много времени. Таким образом, важнейшая задача в расчетах по методу МО ЛКАО ССП – нахождение удачного компромисса между размером базиса и числом подлежащих расчету интегралов.

Существует три основных критерия для оптимального выбора базисных функций: 1) базисные функции должны давать хорошее приближение к истинной волновой функции, т.е. должны правильно моделировать поведение молекулярной системы; 2) базисные функции должны допускать аналитическое вычисление нужных интегралов; 3) полное число базисных функций не должно быть очень большим.

В качестве базиса АО могут быть использованы функции, которые получаются при решении многоэлектронных атомов методом Хартри – Фока. Одними из наиболее известных таких функций являются орбитали Слэтера – Зенера (или просто слэтеровские орбитали, STO):

* Существуют также полуэмпирические методы расчета характеристик молекул или свойств веществ с привлечением экспериментальных данных. По своей сути полуэмпирические методы аналогичны рассмотренным здесь неэмпирическим методам расчета многоатомных молекулярных систем, однако для облегчения расчетов в полуэмпирических методах вводятся дополнительные упрощения. Характеристика основных полуэмпирических методов приведена в Приложении E.

11

где n, l, m – главное, орбитальное и магнитное квантовые числа соответственно; Nn – нормировочный множитель

Ylm(θ, ϕ) – угловая составляющая (сферическая гармоника) та же, что и для водородоподобных функций (см. Приложение С); ζ – орбитальная экспонента

Z – заряд ядра; n* – эффективное главное квантовое число; Sэкр – константа экранирования, которая учитывает сумму вкладов, вносимых отдельными электронами за вычетом рассматриваемого электрона. Величины n* и Sэкр рассчитываются с помощью так называемых

правил Слэтера*.

Форма STO тесно связана с видом орбиталей водородоподобного атома. Поэтому их можно использовать для атомов или небольших молекул. Однако STO недостаточно точно описывают поведение АО Хартри – Фока вблизи ядра. Для устранения этого недостатка можно каждую АО аппроксимировать двумя (или более) слэтеровскими функциями с разными орбитальными экспонентами:

Функции вида (91) называются дубль-зета-функциями, они хорошо аппроксимируют АО Хартри – Фока во всей области изменения r. Базисный набор, составленный из таких функций, называется дубль-зета-базисом (DZ). Существуют также базисные наборы, включающие соответственно три (TZ), четыре (QZ) и т.д. орбитальные экспоненты. Несмотря на высокое качество аппроксимации, достигаемое при использовании DZ-базиса, расчеты с его использованием достаточно сложны, поскольку интегралы перекрывания АО, построенные из STO, нельзя решить аналитически, а численное интегрирование приводит к большим временным затратам.

Очень распространены базисы, в которых используются атомные функции гауссова типа (GTO), которые имеют следующий общий вид

где α – варьируемый параметр. При использовании GTO намного быстрее, примерно в 1000 раз, рассчитываются интегралы. Недостатком гауссовых функций является плохое приближение к АО Хартри – Фока. Поэтому для хорошего описания АО нужно несколько g, называемых примитивными функциями или примитивами. Это приводит к резкому увеличению количества коэффициентов ciν и порядка алгебраических уравнений. Для преодоления этих трудностей некоторые GTO группируют вместе (сжимают) и затем работают как с одной функцией. Например, базисная функция s-типа может быть представлена в виде:

ψ s = ∑ds ,k gs,k , k

где ds,k – фиксированные коэффициенты, k – счетчик примитивных функций. В разложение все примитивные функции gs будут входить с одним коэффициентом ciµ, что уменьшает количество искомых параметров уравнений. Использование различных вариантов сжатия гауссовых примитив привело к появлению большого числа базисных наборов, моделирующих АО.

* Формулировка правил и пример их использования для определения n* и Sэкр, а также построения STO приведены в Приложении F.

12

Один из распространенных методов сжатия – построение минимальных базисов типа STONG, в которых каждая орбиталь слэтеровского типа аппроксимирована N гауссовыми функциями. Это увеличивает число интегралов, однако выигрыш во времени превосходит потери. В большинстве случаев N = 3, т.к. дальнейшее увеличение N не слишком эффективно.

Аккуратный расчет неэмпирическим методом даже простой молекулы еще не так давно являлся дорогостоящей задачей. Однако появление высокоскоростных компьютеров и появление ряда высокоэффективных программных комплексов перевели эту задачу для молекул средней размерности (до нескольких десятков атомов) в разряд рутинных.

Метод ССП широко используется для описания свойств таких молекул, как H2, H2O, CH4, C2H6, C6H6, CO, N2 и NH3. Для таких молекул рассчитанные равновесные расстояния и углы связи отличаются от экспериментальных данных на несколько процентов. Достаточно плохо описываются абсолютные значения полных энергий, однако относительные энергии получаются с хорошей точностью. Точность неэмпирических расчетов, естественно, ограничена приближениями, которые приходится делать для того, чтобы квантовомеханическая задача была решена за разумное время.

3.3.3. Учет электронной корреляции

Целью квантовохимических расчетов является адекватное описание реальных химических систем: точный теоретический расчет строения молекул, их физико-химических свойств, количественное предсказание реакционной способности химических соединений. Метод МО, использующий одноэлектронное приближение, решает часть этих задач. В частности, для подавляющего большинства химических соединений теория хорошо воспроизводит строение, распределение электронной плотности по молекуле, дипольный момент, колебательные спектры и некоторые другие свойства. Ряд задач принципиально не может быть решен с помощью метода Хартри – Фока. В частности, большие проблемы возникают при расчетах полной энергии квантовой системы. Основными источниками погрешностей при расчетах методом Хартри – Фока являются следующие (см. рис. 10):

1)Пренебрежение релятивистскими эффектами при рассмотрении движения электронов. Не вносит большой ошибки.

2)Описание движения электронов в поле покоящихся ядер (приближение Борна- Оппенгеймера). Также не вносит существенной ошибки.

3)Несовершенство базисного набора, моделирующего АО. Эта погрешность расчета энергии очень велика, особенно при использовании простых базисных наборов; она может быть ликвидирована при усложнении базиса и его приближении к совершенному базисному набору.

4)Неадекватное описание коррелированного движения электронов.

Релятивистский эффект

Экспериментальная энергия

Рис. 10. Примерное соотношение теоретических расчетов молекул с экспериментальными данными.

13

Отсюда следует, что, во-первых, для получения сравнимых результатов необходимо использовать намного больше гауссовых функций по сравнению со слэтеровскими, во-вторых, существует точка, ниже которой нельзя рассчитать энергию методом Хартри – Фока. Это так называемый хартри-фоковский предел, обычно рассчитанная в этой точке энергия выше экспериментальной примерно на несколько процентов. Разность энергии между экспериментальной энергией и рассчитанной на хартри-фоковском пределе называется экспериментальной энергией корреляции и определяется непрерывным взаимодействием электронов. Электронную корреляцию можно рассматривать как сумму парных взаимодействий всех электронов молекулы и разделить на две части: внутрипарную, относящуюся к двукратно заселенной МО, и межпарную, которая учитывает взаимозависимое движение электронов различных МО.

Взаимодействия электронов не рассматриваются отдельно в приближении ССП, а оказываются усредненными, так что хартри-фоковская волновая функция не может описать полностью общую энергию молекулы (описывает примерно на 99 %).

Таким образом, для более точного описания молекулярных свойств необходимо учитывать корреляционную энергию. Для этого используют различные методы. Рассмотрим лишь некоторые из них*.

1. Метод конфигурационного взаимодействия (КВ, CI). В данном методе полную волновую функцию записывают в виде линейной комбинации слэтеровских определителей, отвечающих различным электронным конфигурациям:

где M – число учитываемых конфигураций; Ak – коэффициенты. Детерминанты Слэтера Ψk определяются как различные способы размещения электронов по всем орбиталям. Конфигурация Ψ0 соответствует основному состоянию, а остальные – возбужденным состояниям. В зависимости от характера учитываемых возбужденных состояний и количества членов разложения M различают несколько вариантов метода CI. Метод полного КВ (FCI) представляет собой самый полный учет электронной корреляции в рамках используемого базисного набора. В данном методе рассматриваются все возможные состояния: от однократно до n-кратно возбужденных.

Расчеты методами CI широко распространены для учета энергии корреляции. Главная трудность – слабая сходимость представления полной волновой функции в виде ряда детерминантов Слэтера, поэтому необходимо учитывать большое число конфигураций. Это приводит к значительным вычислительным затратам. Например, при использовании FCI для расчета молекулы HF требуется оперировать с 944348 детерминантами.

2. Теория возмущений Мёллера – Плессета (МП, MP). Основная концепция теории возмущений состоит в том, что система, для которой невозможно получить точного решения, делится на две части. Первая, упрощенная часть решаема, а вторая рассматривается как возмущающая часть первой, и к ней применяется аппарат теории возмущений. Полный гамильтониан Hˆ λ , учитывающий энергию корреляции электронов, складывается из хартри-

фоковского гамильтониана Hˆ 0 , для которого известно точное решение уравнения Шрёдингера, и его возмущения:

Возмущенная волновая функция Ψn и En представляются в виде степенного ряда по параметру λ:

* В последние годы одним из наиболее популярных приближений, позволяющим, в том числе, учитывать корреляционную энергию, стала теория функционала плотности (ТФП, DFT). Основы DFT рассмотрены в Приложении G.

14