Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Глава 2

.pdf

Скачиваний:

Добавлен:

11.03.2016

Размер:

416.27 Кб

Скачать

☆

<<< < Предыдущая 12 / 22

3. Любая подпоследовательность фундаментальной последова- тельности фундаментальна.

4Пусть {xn } – фундаментальная последовательность, а {xnk } – ее подпоследовательность. Так как {xn } фундаментальна, то

ε > 0 n0	m,n > n0	xm - xn	< e .	(2.3)

Поскольку количество	членов последовательности			{xn}, не

удовлетворяющих условию (2.3), конечно, то конечным будет и ко- личество членов подпоследовательности {xnk }, не удовлетворяющих

этому неравенству; поэтому можем утверждать, что

"e > 0 $M = Mn0 (e) ³ n0 "nm ,nk ³ M xnm - xnk < e.

Следовательно, подпоследовательность {xnk } фундаментальна.3

4. Если подпоследовательность фундаментальной последователь- ности сходится к A , то и сама последовательность сходится к A.

4Пусть lim x

= A. Покажем, что lim x

= A .

k →∞

n→∞

Зададим некоторое e > 0 . Тогда, по определению предела после-

довательности, $k

"k ³ k

- A

Так как последовательность фундаментальна, то

$n "n ³ n , m ³ n

- x

Положим N0

= max{n0 , nk0 }

nk ³ N0 .

и зафиксируем некоторое

Тогда "n ³ N

x - A

x - x + x - A

- x

- A

+ ε = e ,

то есть lim xn = A .3

n→∞

5. Если {xn }

–

фундаментальная последовательность, то после-

довательность {lxn } также фундаментальна.

4В случае l = 0

фундаментальность {lxn } очевидна. Поэтому

докажем для случая l ¹ 0. Так как {xn} фундаментальна, то

"e > 0

$n = n (e) "m, n ³ n

x - x

n m

Следовательно, "e > 0 $n0

= n0 (e)

"m,n ³ n0

lx - lx

x - x

= e, l ¹ 0 .3

6. Если {xn } , {yn } – фундаментальные последовательности, то последовательность {xn + yn } также фундаментальна.

4Из фундаментальности {xn} следует:

"e > 0

$n = n (e) "m,n ³ n

- x

Из фундаментальности {yn} следует:

< ε .

"e > 0

$n = n (e) "m,n ³ n

- y

Поэтому, "e > 0 $n0 = max{n1(e), n2 (e)} "n,m ³ n0

(xm + ym ) - (xn + yn )

(xm - xn ) + (ym - yn )

x - x

- y

< ε

+ ε

= e .3

Теорема 2.6 (критерий Коши сходимости последовательности).

Числовая последовательность сходится тогда и только тогда, когда она фундаментальна.

4Необходимость. Совпадает со свойством 2.

Достаточность. Пусть {xn } – фундаментальная последователь-

ность. Тогда, в силу свойства 1, она ограничена. По лемме 2.2, огра- ниченная последовательность содержит сходящуюся подпоследова-

тельность {xnk }, а значит, по свойству 4, сама последовательность {xn } тоже сходится.3

Следствие (критерий Коши расходимости последовательности).

Для расходимости последовательности {xn } необходимо и доста- точно, чтобы она не была фундаментальной, то есть

$e > 0 "n0	$n ³ n0	$m ³ n0 и		xn - xm		³ e

или
$e > 0 "n0	$n ³ n0	$k	xn+k - xn		³ e .

П р им е р 2.18. Докажем, что последовательность xn = (-1)n не имеет предела.

4Необходимо показать, что
$e > 0 "n0	$n ³ n0	$k		xn - xn+ k	³ e.
$e > 0 "n0	$n ³ n0	$k		xn - xn+ k	³ e.
Пусть e =1, тогда "n0	xn0 +1 - xn0 +2		= 2 > 1 = e.3
Пусть e =1, тогда "n0	xn0 +1 - xn0 +2		= 2 > 1 = e.3
		55

П р им е р 2.19. Докажем сходимость последовательности

cos1

cos2

+ ...+

cosn

4Оценим модуль разности

xn+k - xn

cos(n +1)

+...+

cos(n + k )

n+1

n+k

+ ...+

1-1/3k

3k -1

3n+1

3n+k

3n+1

×3n

1-1/3

n+1

×3

Так как

lim

= 0, то "e >0 $n "n³n

<e . Поэтому, если

n→∞

n³n , а k – произвольное натуральное число, то

- x

< e.

n+k

Таким образом, последовательность {xn }

сходится в силу крите-

рия Коши.3

П р им е р

2.20. Докажем,

что последовательность

xn = sin

πn не

имеет предела.

4Необходимо показать, что

$e > 0 "n0 $n ³ n0

xn - xn+k

³ e .

Пусть e =

, тогда при любом n

будем иметь

p(6n0 +1)

p(6n0 + 3)

- x

sin

-sin

6n0 +1

6n0 +3

=3 2 - 0 = 3 2 > 12 = e.3

Пр им е р 2.21. Докажем расходимость последовательности

xn = 1+ 12 + 13 + ...+ 1n .

4Оценим модуль разности

xn+k - xn = n1+1 + n 1+2 + ...+ n 1+k ³ n 1+k + n +1 k + ...+ n +1 k = n +k k .

14444244443

k штук

Если взять k = n , получим

- x

= 1 . Следовательно,

n + n

данная последовательность удовлетворяет критерию Коши расхо-

димости последовательности:

$e =

"n $n = n $k = n

n+k

- x

2n0

2.9*. ПРИМЕРЫ СХОДЯЩИХСЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ

П р им е р 2.22. Докажем, что lim

= 0.

4Пусть m ¥ и m >

n→∞ n!

. Тогда

0 <

m +1

a	m æ		a	ön−m
a	m æ		a	ön−m
		ç		÷ .


m! è m +1				ø

Так как

< 1, то ε > 0 при достаточно больших n справедли-

m +1

m æ

ön−m

во неравенство

< e , и, следовательно,

lim

= 0 (при

m! è m +1

n→∞ n!

фиксированном e > 0

неравенство

выполняется

начиная с

номера

em!

+ m , где c =

).3

= êlog

ú +1

m +1

П р им е р 2.23. Докажем, что lim

= 0, при a > 1.

n→∞ an

4Пусть m Î ¢, m ³ b. Тогда

öm

æ n öm

(2.4)

0 <

= ç

è m an

è c

где c = m

>1. Но

0 <

(

c -1

))

. (2.5)

n(n -1)

(n-1)(c -1)2

1+n(c -1)

(c -1)

+L+ (c -1)

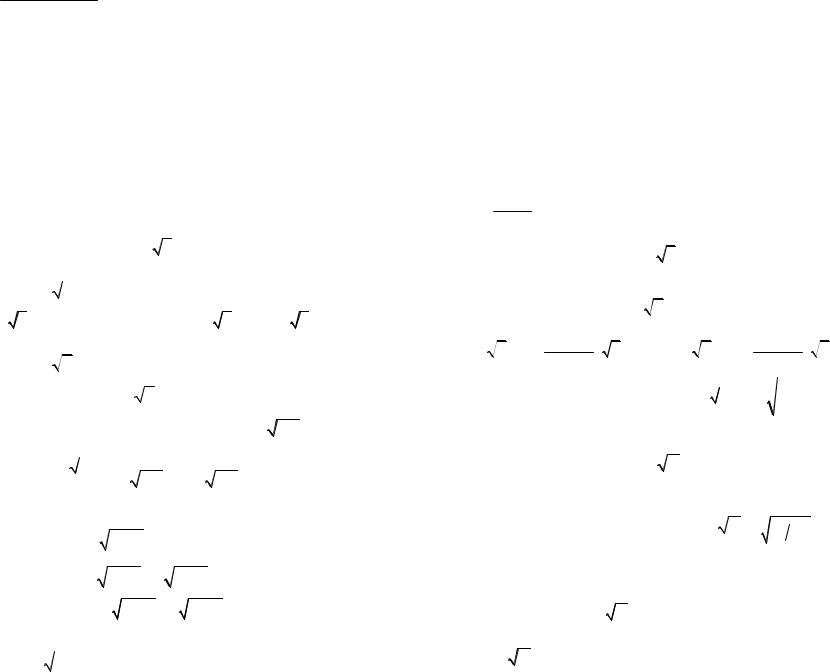
Так как	2n	® 0 при n → ∞ , то, в силу теоремы о
	n(n -1)(c -1)2

трех последовательностях, из (2.5) следует, что						n	® 0 при n → ∞ ,
						cn
	æ n öm

а значит,	ç		÷	® 0 при n → ∞ . Тогда из (2.4)	(опять по теореме о
		n
	è c	ø

трех последовательностях) получаем требуемое утверждение.3

П р им е р 2.24. Докажем, что limnqn

= 0, если

< 1.

n→∞

4Доказательство аналогично предыдущему, если учесть, что

nqn

, b > 1.3

(1/ q)n

П р им е р 2.25. Докажем, что lim n

= 1.

n→∞

41) При a = 1 равенство очевидно.

2) Если a > 1, то n a > 1 и

éНеравенствоù

a = (1+ (

a -1))

³ 1+ n(

a -1) > n(

a -1).

³ ê Бернулли ú

Следовательно, 0 < n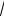a -1 < an < e при n > ae (ε > 0 ), то есть

lim n a =1.

n→∞

3) Если 0 < a < 1, то

> 1 и, по доказанному, lim n

= 1. Тогда

1/ a

n→∞

lim n

= lim

= 1.3

n→∞

n→∞ n 1/ a

lim n 1/ a

n→∞

П р им е р 2.26. Пусть lim x = 0 и "n x ³ -1. Докажем, что

n→∞

lim p

1+ x

=1,

p > 0.

n→∞

£ (p

)p =1 + xn =1+

41) Если xn ³ 0 , то 1 £ p

1+ xn

2) Если -1 £ xn

< 0, то 1 ³ p

³ (p

=1 + xn =1-

1+ xn

Так как lim xn

= 0 , то

lim

= 0

и lim(1+

) = lim(1-

) = 1,

n→∞

следовательно, lim p

1+ x

=1.3

n→∞

П р им е р 2.27. Докажем, что lim	loga n	= 0, a > 1.
	n
n→∞

4Так как lim	n		= 0 , b > 1 (см. пример 2.23), то при достаточно
4Так как lim			= 0 , b > 1 (см. пример 2.23), то при достаточно
n→∞ bn							1		n
большом n справедливо неравенство							1	<	n	< 1. Положим b = aε ,
большом n справедливо неравенство							bn	<		< 1. Положим b = aε ,
							bn		bn
где a > 1, а ε > 0 – произвольное. Тогда
		1		<	n	< 1 или 1 < n < aεn .
			aεn	<		< 1 или 1 < n < aεn .
			aεn		aεn

Прологарифмировав последнее неравенство, получим

0 < loga n < en ,

откуда 0 < loga n < e при достаточно большом n. 3 n

П р им е р 2.28. Докажем, что lim n n = 1.

n→∞

4Из неравенства

n= (1+(nn -1))n=

=1+ n(nn -1)+ n(n2-1)(nn -1)2+...+ (nn -1)n> n(n2-1)(nn -1)2

следует, что ε > 0 $n = 1+

ù "n ³ n

-1

< e.3

n -1

ëe

П р им е р 2.29. Докажем, что lim

= 0 .

n→∞ n n!

4Ранее было доказано (см. следствие 3 из теоремы 2.4) неравен-

æ n ön

ство ç

÷ < n!, из которого следует, что

0 <

è e ø

n n!

n (n e)n

Следовательно, ε > 0 при всех n >

(или

ε ), получим

0 <

< e

= e,

n n!

а значит, lim

= 0 .3

n→∞ n n!

П р им е р 2.30. Пусть	0 < x1 < 1, xn+1 = xn (2	- xn ). Докажем, что
последовательность {xn }	сходится, и найдем ее	предел при n → ∞ .

4Докажем сначала, что данная последовательность ограничена,

а именно,
"n 0 < xn <1.	(2.6)

Для этого применим метод математической индукции. Согласно условию, для n = 1 требуемое неравенство выполнено. Пусть оно верно для n = k . Тогда очевидно, что для n = k +1

xk +1 = xk (2 - xk ) > 0 .

Остается показать, что xk +1 = xk (2 - xk ) < 1. Действительно, нера-

венство	xk (2 - xk ) < 1 преобразуется к неравенству -(xk -1)2 < 0 , ко-
торое верно с учетом неравенства xk				¹ 1. Таким образом, "n 0 < xn <1.
Исследуем исходную последовательность на монотонность:
	xn+1 - xn = xn (2 - xn ) - xn		= xn (1- xn ) > 0 при 0 < xn < 1.
Следовательно, эта последовательность возрастающая.
Итак,		мы показали, что последовательность						xn+1 = xn (2 - xn ),
0 < x1 <1		возрастает и ограничена, а значит, сходится, согласно тео-
реме Вейерштрасса, то есть lim x				= a .
		n→∞	n
Переходя к пределу в равенстве xn+1 = xn (2 - xn )								и учитывая, что
lim x	= a , получаем a = a(2 - a), откуда находим, что a = 0 или
n→∞ n+1
a = 1. Так как последовательность { xn } возрастающая, то
		n a > xn > x1 > 0 ,
поэтому lim x = 1.3
		n→∞ n
П р им е р 2.31. Пусть x = 1,			x		=1+	1	. Докажем, что последо-

		1	n+1

вательность {xn } сходится и найдем ее предел при n → ∞ . 4Рассмотрим отдельно четную и нечетную подпоследователь-

ности данной последовательности:

xn +1

n+2

xn+1 +1

2xn +1

, x = 1, x = 2.

xn+1

xn +1

Исследуем каждую из этих последовательностей на монотонность.

xn+2 - xn =

2x +1

- xn

-x2 + x +1

xn +1

öæ

-ç xn

÷ç xn -

øè

xn +1

- x

при x

Î(-¥,-1)U

1+ 5

n+2

> 0

÷,

(2.7)

1 -

æ1+

- x

при x

< 0

Îç

-1,

÷ U

,+¥

÷.

(2.8)

n+2

ø è

Используя метод математической индукции, покажем, что n

1 £ x

. Согласно условию, для n = 1 требуемое неравенст-

2n−1

во выполнено. Пусть оно верно для n = k . Тогда очевидно, что для

n = k +1, с учетом (2.7), x2k +1 > x2k −1 ³ 1. Остается показать, что

x2k +1 <

Действительно, пусть

это

не

выполняется, то

есть

неравенство

x2k +1 ³

. Тогда

2x2k −1 +1

1 +

, что эквивалентно неравенству

x2k −1 +1

(

-1)(3 +

)

-1

2k −1

- 5 (3 - 5 )(3 + 5 )

которое противоречит сделанному выше предположению. Таким образом,

n 1 £ x2n−1 < 1+2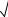5 .

Следовательно, нечетная подпоследовательность исходной по- следовательности возрастает и ограничена, а значит, сходится, со-

гласно теореме Вейерштрасса, то есть lim x2n−1 = a . Отметим, что

n→∞

1 £ a £ 1+ 5 по свойствам пределов. 2

Аналогичным образом можно показать, что

n 1+2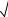5 < x2n £ 2.

Следовательно, с учетом (2.8), четная подпоследовательность ис- ходной последовательности убывает и ограничена, а значит, сходит-

ся, согласно теореме Вейерштрасса, то есть lim x2n

= b . Отметим, что

n→∞

по свойствам пределов

£ b £ 2.

2xn +1

Переходя к

пределу в

равенстве

xn+2 =

учитывая,

что

xn +1

lim x

= a, lim x

= b , получаем

a =

2a +1

b =

2b +1

откуда

n→∞ 2n+1

n→∞ 2n+2

a +1

b +1

находим,

что

a =

1±

b =

1±

Так

как

1 £ a £

£ b £ 2, то a = b = 1+

. Значит, исходная последовательность

сходится, согласно следствию 1 теоремы 2.5, и lim x

n→∞

П р им е р 2.32. Найти lim xn , если последовательность {xn} задана
соотношениями x	n→∞		= 0.5x2	-1.
	= 1/3, x	n
0			n−1

4Разобьем эту последовательность на две подпоследовательно-

сти {x2k } и {x2k −1} . Если они обе сходятся к одному пределу, то и

исходная последовательность тоже сходится к этому пределу. Если будет доказано, что у последовательностей {x2k } и {x2k −1} предел

существует, то его можно вычислить следующим образом. Пусть

a = lim x	n	, тогда a = lim x = 0.5lim x2			-1 = 0.5a2 -1.
n→∞			n→∞ n	n→∞ n−1
Решая квадратное уравнение, получим a =1-							3	или a =1+	3	.
Легко показать,			что если	xn−1 Î(-1,0) , то и		xn Î(-1,0) . Так как
x1 ≈ −0.94 , то			последовательность		может	сходиться только			к

a =1- 3 .

Рассмотрим отдельно четную и нечетную подпоследовательно- сти данной последовательности.

xn+2 = 18 (xn4 - 4xn2 - 4), x1 ≈ −0.94 , x2 ≈ −0.56.

Исследуем каждую последовательность на монотонность.

xn+2 - xn =

(xn4

- 4xn2 - 4)- xn

xn4 - 4xn2 - 4 -8xn

- 4(xn2 + 2xn

+1)

(xn -(1+

))(xn - (1-

))(xn2 + 2xn + 2)

xn4

Таким образом, если все элементы последовательности принад-

лежат промежутку

ë1- 3, 0), то последовательность убывает, а ес-

ли все

элементы

последовательности принадлежат

промежутку

(-1,1-

3û, то последовательность возрастает.

Функция f (x)

x4 - 4x2 - 4

на промежутке (-1,0)

возрастает,

поэтому

"x Î(

-1,1-

f (x) < f (1- 3) =1- 3

3û

"xÎ

- 3 = f (1- 3)< f (x).

ë1- 3, 0) 1

Следовательно, последовательность {x2k } убывает и ограничена снизу величиной 1- 3 , а последовательность {x2k −1} возрастает и

ограничена сверху величиной 1- 3 . Обе последовательности схо- дятся, и их предел 1- 3 .3

2.10. ОТКРЫТЫЕ И ЗАМКНУТЫЕ МНОЖЕСТВА

Напомним, что точка x0 называется предельной точкой множе-

ства X , если любая окрестность этой точки содержит бесконечное множество точек из X или, что то же самое, в любой окрестности точки x существует по крайней мере одна точка множества X , не совпадающая с x0 , то есть "e > 0 $x Î X , x ¹ x0 x - x0 < e. Пре-

дельная точка может как принадлежать, так и не принадлежать множеству X .

Символ (+¥) называют предельной точкой (предельным зна-

чением) множества X , если E ¡ x X x > E .

Символ (-¥) называют предельной точкой (предельным зна-

чением) множества X , если E ¡ x X x < E .

Точка x0 X , не являющаяся предельной точкой множества X , называется изолированной точкой множества X , то есть ε > 0

"x Î X {x ¹ x0 Þ x Ï(x0 - e, x0 + e)} .

Точка x0 ¡ называется:

– внутренней точкой множества X , если

ε > 0 "x Î¡ x - x0 < e Þ x Î X ;

– внешней точкой множества X , если

ε > 0 "x Î¡ x - x0 < e Þ x Ï X ;

– граничной точкой множества X , если она не является ни внут- ренней, ни внешней, то есть

ε > 0	$x1 Î X		x1 - x0		< e Ù $x2 Ï X		x2 - x0		< e.

З ам е ч а н и е 1		. Всякая внутренняя точка является предельной.
З ам е ч а н и е	2	. Всякая изолированная точка является граничной.
З ам е ч а н и е	3	. Всякая граничная точка не является внутренней.
Множество всех граничных точек множества X называется гра-

ницей множества X . Множество X называется открытым, если все его точки внутренние. Множество X называется замкнутым, если оно содержит все точки своей границы или, что то же самое, все свои предельные точки.

З ам е ч а н и е . Множества ¡ и являются и открытыми и замк-

нутыми одновременно.

П р им е р 2.33. Рассмотрим множество X = [2,3).

41. Все точки множества

X –

предельные,

так

как если

x0 Î[2,3), то

min{e, 3 - x0}

"e > 0 $x = x +

, x

X ,

x - x

< e, x

¹ x .

Кроме того, предельной является точка x0 = 3, так как

"e > 0 $x = 3-

min{e,1}

, x X , x ¹ x ,

x - x

< e.

2. Точки множества (2,3) – внутренние точки множества X , так

как если x0 Î(2,3), то

$e =

min{3 - x0 , x0 - 2}

"x Î¡

x - x0

< e Þ x Î X .

3. Изолированных точек нет, так как все точки множества X яв-

ляются предельными.

4. Точки x0 = 2 и x0

= 3 – граничные, так как:

а) ε > 0

= 2 +

min{e,1}

x Î X , x

¹ x ,

x - x

< e

$x = 2 -

Ï X , x

¹ x ,

x - x

< e ;

б) ε > 0

= 3 -

min{e,1}

x Î X , x

¹ x ,

x - x

< e

$x = 3 +

x Ï X , x

¹ x ,

x - x

< e.3

П р им е р 2.34. Рассмотрим множество X = {5} U[1,4].

41. Точки отрезка [1,4] –

предельные

точки

множества

X ,

так как если x0 Î(1,4], то

{

e, x -1

min

"e > 0 $x = x -

}

x X , x ¹ x ,

x - x

< e,

а если x =1, то "e > 0

min{e, 3}

x X , x ¹ x

< e.

$x = 1+

x - x

2. Точки множества (1,4) –

X ,

внутренние точки множества

так как если x0 Î(1,4), то

min

{

4 - x , x -1

$e =

}

"x Î¡

x - x0

< e Þ x Î X .

3. Точка x0

= 5 – изолированная точка множества X , так как

$e =

> 0 "xÎ X x

¹ 5 Þ x Ï

; 5

ç5 -

÷.

4. Точки x0

=1, x0 = 4 и x0

= 5 – граничные, так как:

а) ε > 0

= 1+

min{e,1}

x Î X , x ¹ x ,

x - x

< e и

= 1-

Ï X , x ¹ x ,

x - x

< e ;

б) ε > 0

= 4 -

min{e,1}

x Î X , x

¹ x ,

x - x

< e и

= 4 +

min{e, 1}

Ï X ,

¹ x

- x

< e;

в) Точка x0 = 5 изолированная и, следовательно, граничная.3

Пр им е р 2.35. Интервал (2,3) является открытым множеством, поскольку все его точки – внутренние.

Пр им е р 2.36. Отрезок [1,4] – замкнутое множество. Выше было

показано, что все точки отрезка являются предельными, поэтому достаточно показать, что других предельных точек нет. Действи-

	ì(1- x		)/ 2, x < 1;
тельно, пусть x0 Î ¡ \ [1,4] . Тогда $e =	ï	0	0	такое, что
тельно, пусть x0 Î ¡ \ [1,4] . Тогда $e =	ïí(x0 - 4)/ 2, x0 > 4			такое, что
	î

"x Î X x - x0 > e, а значит, x0 не может быть предельной точкой.

П р им е р 2.37. Полуинтервал [2,3) не является ни открытым, ни

замкнутым множеством, поскольку он содержит граничную точку x0 = 2, но не содержит граничную точку x0 = 3.

Теорема 2.7. Пусть S – предельная точка множества X ¡. Тогда существует последовательность {xn } , сходящаяся к S , все

элементы которой отличны от S , то есть

1) xn ® S при n → ∞ ; 2) "n xn Î X , xn ¹ S .

4Построим эту последовательность.

1. Если S = x0 Î ¡, то по определению предельной точки полу-

чим, что ε > 0, а значит и для ε = 1,

$x1 Î X

такой, что x1 ¹ x0

x1 - x0

< e =1. Аналогично, для ε = 1/2

$x2 Î X

такой, что x2 ¹ x0

x2 - x0

< e = 1/ 2 , и т.д. для ε = 1/3,1/ 4, ... Тогда

ε > 0 $n =

é1

ù +1 "n > n

x - x

< 1 <

< e.

n n0

ë3

2. Если S = +∞, то по определению предельной точки получим,

что E > 0 , а значит и для

E = 1, $x1 Î X

x1 > E = 1. Аналогично,

для E = 2, $x2 Î X

x2 > E = 2, и т.д. для E = 3, 4, 5, .... Тогда

E > 0

$n0 = [E] +1 "n > n0 xn > n > n0 > E .

3. Если S = −∞, то по определению предельной точки получим, что E > 0 , а значит и для E = 1, $x1 Î X x1 < -E = -1. Аналогично,

для E = 2, $x2 Î X x2 < -E = -2 , и т.д. для E = 3,4,5,.... Тогда

E > 0 $n0 = [E] +1 "n > n0 xn < -n < -n0 < -E .3

<<< < Предыдущая 12 / 22

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
27.03.20151.51 Mб282Гильмундинов-Мельников.pdf
#
27.03.2015148.54 Кб7глава 2.docx
#
11.03.2016478.69 Кб23Глава 1.pdf
#
27.03.2015184.32 Кб11Глава 10.doc
#
11.03.2016780.58 Кб10Глава 2.pdf
#
11.03.2016416.27 Кб9Глава 2.pdf
#
11.03.2016546.03 Кб8Глава 3,4.pdf
#
11.03.2016719.99 Кб7Глава 3.2.pdf
#
11.03.2016746.33 Кб8Глава 3.pdf
#
11.03.2016911.85 Кб7Глава 5.pdf
#
11.03.2016660.06 Кб5Глава 6.pdf