
Organizatsionno-upravlencheskie_reshenia / Управленческие решения_Балдин К.В, Воробьев С.Н, Уткин В.Б_Учебник_2006 -496с
.PDF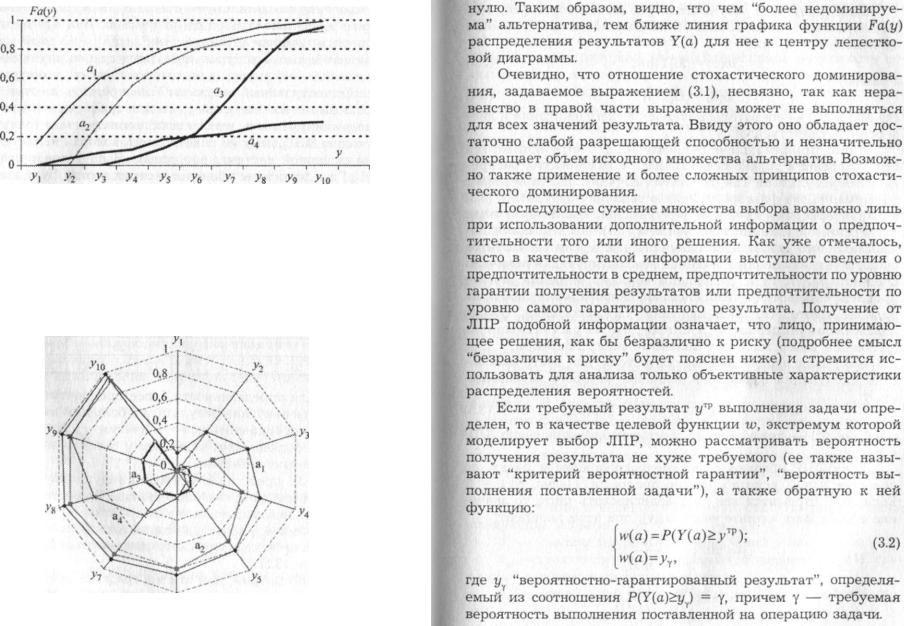
Рис. 3.4. Графики функций распределения результатов для альтернатив
нируемой альтернативы а: занимает положение на перифе рии области лепестковой диаграммы ближе к значениям, рав ным единице. Графики функций Fa(y) распределения резуль татов Y(a) для недоминируемых альтернатив концентрируют ся ближе к центру диаграммы, где значения функции равны
Рис. 3.5. Лепестковая диаграмма
222 |
223 |

224 |
225 |

P(H,/D)=-
227

После получения информации о событии /5 пороговое значение R T P еще не преодолено. Но при этом абсолютное значение вероятности истинности гипотезы Н1 ("конъюнкту ра рынка благоприятна") у ж е почти 0,8, и, следовательно, ЛПР может принять решение о том, что установлен практи-
229

230 |
231 |

И еще одно важное замечание. Поскольку детерминиро ванный эквивалент — неслучайная величина, это позволяет легко свести задачу обоснования решений в условиях стохас тического риска к задаче принятия решений в условиях оп ределенности. Надо только все случайные исходы заменить их детерминированными эквивалентами. После этого формаль ный анализ проводят как бы в условиях определенности.
3.3. Технологии принятия решений в условиях поведенческого риска
Пусть теперь главным фактором, определяющим "меха низм проблемной ситуации", оказывается поведение одного или нескольких субъектов, оказавшихся втянутыми в опера цию ЛПР и вынужденных взаимодействовать с ним, возмож но, даже против своей воли. Чтобы при изложении материа ла однозначно понимать, кто есть кто, будем ЛПР, в инте ресах которого мы вырабатываем решения, называть "наше ЛПР", а остальных самостоятельно действующих суверен ных субъектов — "другие ЛПР". Эти "другие ЛПР" на самом деле могут и не противостоять "нашему ЛПР", и не желать ему зла. Однако "нашему ЛПР" при обосновании им своих решений важно знать, как эти "другие" поступят или могут поступить. Если такой информации у "нашего ЛПР" не б у дет, то у него не будет иного выхода, как воспринимать "других ЛПР" как агрессивную среду.
Причин подобного отношения к проблемной ситуации у ЛПР может быть несколько:
• ''наше ЛПР" точно знает, что его интересы вошли в противоречие, столкнулись с интересами "других ЛПР";
• "наше ЛПР" не знает, являются ли его устремления конфликтующими с интересами "других ЛПР", однако что-то заставляет его опасаться, что это так;
|
• "наше ЛПР" знает, что его интересы совпадают с ин |
|
тересами "других ЛПР", что объективно оно желает |
232 |
233 |
им добра, однако эти "другие Л П Р " могут этого не понять или не принять из-за различия в позициях, т о чек зрения, культурных традиций, а это обязательно приведет к столкновению;
• "наше Л П Р " знает, что иных субъектов кроме него в операции нет и действовать оно будет в объективной обстановке ("в природе"); однако эта "природа" — "terra incognita". Поэтому ЛПР опасается подобной неопреде ленности, непредсказуемости, боится ее. Из-за этого ЛПР вынуждено считать "природу" как бы агрессив ной, принимать ее возможные проявления как дей ствия агрессивно настроенного "другого ЛПР".
Разработкой технологий и методов разработки решений в перечисленных проблемных ситуациях занимаются психоло гическая теория решений и теория игр. Но это своеобразные и сложные дисциплины. Воспользоваться напрямую резуль татами этих двух теорий обыкновенному управленцу, не спе циалисту по ТПР, не математику подчас довольно трудно. Например, только по - крупному в психологической теории решений выделяют психологию поведения индивида, психо логию малых групп, психологию масс. В теории игр аналогич но рассматривают игры двух и N лиц, антагонистические и неантагонистические игры, матричные, биматричные, о п е ративные игры и т. д. Даже альтернативы ЛПР в теории игр принято называть стратегиями, чтобы подчеркнуть принци пиальное отличие подобных проблемных ситуаций от иных. Не раз в литературе подчеркивалось, что именно в подоб ных проблемных ситуациях значительную роль в выборе наи лучшей стратегии играют искусство, интуиция, мнения и ил люзорные оценки ЛПР, а не наука, не строгий расчет, не строгие измерения. Однако современные достижения в т е о рии игр более чем скромны, если применять критерии типа "искусство", "интуиция", "мнения" и т. п. В общем, трудно не специалисту! А как же быть? Постараться применить м о делирование.
234
Модельными компонентами теории игр являются игро ки, цели игроков, доступная игрокам информация для при нятия решений и правила реализации игроками собственных стратегий (осуществления ходов в игре).
В зависимости от того, как конкретно сочетаются пере численные элементы игр, их относят к тому или иному клас су. В качестве классификационных признаков, характеризу ющих ту или иную игру, обычно используют [39]:
•количество субъектов (игроков), интересы которых за трагиваются при проведении операции и которые м о гут влиять на ее результаты, а также возможность создания коалиций игроков;
•тип отношений м е ж д у игроками, возникающих при стремлении игроков обеспечить наивыгоднейшее поло жение в игре для себя;
•возможность обмена информацией между игроками в целях сообщения своих возможных стратегий и оце ночных функций;
•возможность образования коалиций игроков;
•типы множеств стратегий игроков;
•типы шкал для описания функций выигрышей игроков;
•возможность провести лишь небольшое количество (в частности — только одну) или достаточно много партий игры.
Например, по количеству игроков выделяют парные и множественные игры (игры N лиц); по типу отношений м е ж ду игроками — игры со строгим соперничеством, нестрогим соперничеством или содействием друг другу; по возможнос ти обмена информацией между игроками — кооперативные и некооперативные; по возможности образования коалиций иг роков — коалиционные и бескоалиционные и др. Что касает ся типов шкал для описания функций выигрышей игроков, то различают игры с предпочтениями (шкалы качественные) и игры с полезностями (шкалы количественные).
Изучить все типы игр одинаково хорошо и сразу вряд ли удастся. Как всегда, следует сосредоточиться на чем-то и
235
пожертвовать чем - то другим. При этом по-прежнему глав ным ключом разрешения этого познавательного затруднения следует выбрать уровень иерархии управления "нашего ЛПР" и перечень решаемых им задач.
Так, например (см. рис. 3.1), мы у ж е отмечали, что " И с полнителю" почти не приходится сталкиваться с поведенчес кой неопределенностью. А вот если взять концептуальный уровень типа "Администратор", то здесь все как раз наобо рот. Как правило, главный тип неопределенности, с которым приходится сталкиваться такому "нашему ЛПР" — это "Кон фликт". Теперь можем уточнить, что обычно это нестрогое соперничество. Несколько реже "Администратор" принимает решения в условиях "природной неопределенности", и еще реже он сталкивается со строгим, антагонистическим конф ликтом. Кроме того, столкновение интересов при принятии решений "Администратором" происходит, так сказать, "од нократно", т. е. в нашей классификации он чаще разыгрывает только одну (иногда весьма небольшое количество) партий игры. Шкалы для оценки последствий чаще качественные, чем количественные. Стратегическая самостоятельность у "Администратора" довольно ограничена. Принимая во вни мание сказанное, можно утверждать, что проблемные ситу ации подобного масштаба чаще всего приходится анализиро вать с помощью бескоалиционных неантагонистических би матричных игр, причем, в чистых стратегиях [39].
Если рассматривается проблемная ситуация на уровне "Руководитель звена отрасли", то здесь примерно одинако во часто приходится сталкиваться с природной неопределен ностью или строгим конфликтом с повторяющимися ситуаци ями. Адекватными здесь будут методы теории игр с природой и решения матричных или биматричных игр в смешанных стратегиях.
Для обоснования решений на уровне "Высшее руковод ство" в наибольшей степени подходят модели биматричных игр с угрозами, модели группового выбора и игр N лиц, а также особый игровой подход к разрешению поведенческой неопределенности — деловые беседы.
236
3.3.1. Технология предварительного анализа проблемной ситуации с использованием теории матричных игр
Разработку решений в условиях поведенческой неопре деленности целесообразно декомпозировать по этапам у с л о ж няющегося использования информации о проблемной ситуа ции. На первом этапе целесообразно провести предваритель ный анализ собственных стратегических возможностей при упрощенном подходе к обоснованию решений в схеме "один против всех". При этом для повышения надежности представ лений, выводов и рекомендаций целесообразно предваритель ные оценки получить в качественных шкалах и без учета п о ведения "других ЛПР" как самостоятельных субъектов. За тем следует уточнить шкалы измерения предпочтений, а за тем на основе дополнительной информации или рефлексий уточнить собственные предпочтения и предпочтения отдель ных субъектов среди "других ЛПР". На завершающем этапе разработки решений следует оценить возможности блефа, угроз, кооперирования и вступления в коалиции с некоторы ми из "других ЛПР". В целом использование принципов р е ф лексии и адаптации потенциально позволяет существенно повысить ожидаемую выгодность будущей стратегии поведе ния "нашего ЛПР".
Итак, предварительный формальный анализ проводим в наиболее простой форме, а именно — для однократно р а зыгрываемой парной бескоалиционной некооперативной игры со строгим соперничеством и дискретными множествами стра тегий игроков. Математической формой такой конфликтной ситуации является матричная игра в чистых стратегиях.
Матричные игры исследуют на основе принципа наиболь шего гарантированного результата. Понятие гарантирован ного результата базируется на гипотезе о крайне неблаго приятном стечении обстоятельств для ЛПР. Согласно прин ципу наибольшего гарантированного результата рациональ ным следует считать такое поведение, которое обеспечивает
237
наилучший из самых неблагоприятных результатов. В силу этого данный принцип часто называют принципом максимина (хотя, как это будет показано ниже, подобное у т в е р ж д е ние не всегда семантически корректно). Помимо принципа наибольшего гарантированного результата руководствуются также принципом равновесия. Принцип равновесия означа ет, что рациональным поведением субъектов операции сле дует считать такое, при котором каждый из них стремится к ситуации, обеспечивающей ему наибольший гарантированный результат, отклонение от которой невыгодно никому.
Количественный анализ на основе применения принци пов наибольшего гарантированного результата и равновесия ведется по следующей технологической схеме:
• формирование игры, т. е. множеств возможных страте гий игроков;
• оценка величин результатов, получаемых субъектами в каждой из ситуаций (предпочтительнее качествен ная шкала);
•выделение множества недоминируемых стратегий для каждого из игроков;
•выбор наилучшего варианта решения на основе прин ципов наибольшего гарантированного результата и рав новесия.
Рассмотрим методы, реализующие представленную тех нологию.
Пусть первый игрок — это "наше ЛПР", а все осталь ные (если их несколько) — "другое ЛПР", или — второй игрок. Обозначим через А и В множества стратегий первого и второго игроков соответственно. Для проведения формально го анализа обозначим через vx(a, b), v2(a, b) оценочные ф у н кции игроков, заданных на множестве (а, Ъ) ситуаций игры. Эти функции скалярные, шкала их значений должна позво лять оценивать как минимум "Тенденции" (напомню, что о сути технологии "Номинации—Тенденции—Пропорции" мы го ворили в п. 1.2.3. Качественная шкала "тенденций" позволит сравнительно легко упорядочить ситуации (а, Ь) игры по
238
предпочтительности. Затем на качественной шкале вводят градации, чтобы можно было бы выявить хоть какие-то про порции. Далее вводят допущение о том, что первый игрок выигрывает ровно столько, сколько ему проигрывает второй, и на этом основании полагают v}(a, b) = - vja, Ъ). После этого можно оставить только одну из оценочных функций, напри мер функцию первого игрока, которая будет адекватно опи сывать предпочтительность исходов игры. Для определеннос ти будем полагать, что это функция v(a, Ъ) = vx{a, Ь), т. е. она совпадает с оценочной функцией первого игрока.
Чтобы сформировать матричную игру, сначала нужно сформировать множества стратегий игроков. Каждое из них должно быть обозримым. Достичь этого можно благодаря принципам цели, декомпозиции и композиции.
Как нам известно, любая альтернатива ЛПР может быть
описательно |
задана |
следующими |
основными |
ее элементами: |
|
• |
что сделать? — определяется целью предстоящих дей |
||||
|
ствий; |
|
|
сделать? — |
диктуется о б |
• |
когда? |
где? с |
помощью чего |
||
стоятельствами времени, места, характеристиками име ющегося активного ресурса;
• на что направить усилия? — определяется объектом приложения усилий.
Если зафиксировать некоторые из перечисленных эле ментов альтернативы, а остальные изменять по определен ным правилам, то можно формировать различные варианты действий.
Именно эта схема положена в основу большинства из известных методов формирования вариантов решения, одна ко все .они различаются степенью формализации основных операций (см. п. 1.3.3). Обычно при формировании игры эврис тические методы применяют одновременно с рефлексивны ми, которые как раз и ориентированы на случай, когда веду щим типом неопределенности является поведенческая.
Вначале эвристически формируют множество стратегий первого игрока. В него включают альтернативы, которые обес -
239

печивают достижение цели первого игрока хотя бы в прин ципе. Затем из полученного множества отсеиваются физичес ки нереализуемые альтернативы, т. е. те, которые не могут быть осуществимы в отведенные на операцию сроки. Полу ченное множество дополняют альтернативами, придающими стратегиям гибкость и устойчивость. При этом руководству ются двумя основными идеями. Во-первых, стремятся обес печить некую инвариантность, примерно одинаковую прием лемость альтернатив ЛПР по отношению к изменяющимся или неизвестным на данный момент составляющим условий проведения операции. Предпочтение следует отдавать тем стратегиям, которые можно оперативно, сравнительно про сто и с незначительными потерями ресурсов скорректиро вать, когда прояснится обстановка. Во-вторых, следует вни мательно изучить всю информацию о личности второго игро ка. Главное внимание при этом сосредоточить на его мораль но-ценностных ориентирах и предпочтениях, сделать выво ды о его подозрительности или доверчивости, самоуверенно сти или нерешительности, его склонности или несклонности к риску и др.
Выводы из подобной оценки помогут первому игроку э ф фективно использовать блеф и сгенерировать достаточное количество псевдостратегий. При генерации псевдостратегий следует помнить важный принцип блефа: все, что привлека ет внимание конкурента, может быть использовано в каче стве приманки. Например, тщеславного, самоуверенного, рискованного субъекта с низкими моральными качествами, несомненно, соблазнит то, что вы, как его конкурент, выг лядите слабым, неопасным и даже — не очень привлека тельной жертвой. В подобной ситуации такое ваше поведе ние обычно провоцирует самоуверенного конкурента не очень скрывать от вас свои планы, подталкивает его к использова нию не самых сильных его стратегий. Наоборот, если конку рент осторожен, неуверен, чрезмерно пессимистичен и т. п., вам следует показать себя сильным, решительным, готовым к самым безрассудным поступкам. Тогда вы сможете доста-
240 |
241 |
|
