Лекция дискрет 05

Следствие

Любое бесконечное подмножество счётного множества счётно

Непосредственно из Th.1.4.6 следует, например, счётность следующих множеств натуральных чисел:

множество чётных чисел { n: n = 2 k, k=1,2,… }

множество нечётных чисел { n: n = 2 k+1, k=0,1,2,… } множество квадратов натуральных чисел { n: n = k2, k=1,2,… }

множество простых чисел

множество составных чисел

Идея построения нумерации некоторого множества М (по аналогии с Th.1.4.6):

1. Вводим целочисленную характеристику элементов нумеруемого множества М, например: если это натуральные числа, как в Th.1.4.6 – само число; сумма координат – для векторной величины с целыми компонентами; сумма модулей числителя и знаменателя – для рациональной дроби; …….

2. Строим соответствие, нумеруя элементы множества М в порядке возрастания введённой в п.1 их целочисленной характеристики

3. Доказываем взаимно однозначность построенного соответствия. Всюду определённость и сюръективность на бесконечных множествах обосновываем с использованием следующего рассуждения:

Для всякого, сколь угодно большого, натурального числа в множестве М имеется конечное количество меньших его натуральных чисел, поэтому любому элементу из М при этой процедуре через конечное число шагов будет присвоен номер.

Пример: Счётность множества рациональных чисел

Рациональное число (лат ratio - отношение, деление, дробь) - число, представляемое (несократимой) обыкновенной дробью m/n, числитель m - целое число, а знаменатель n - натуральное число (предполагается единственный способ представления нуля, а именно 0/1)

В качестве «веса» дроби примем сумму модуля числителя и знаменателя, при равенстве суммы считаем меньшей дробь с меньшим числителем.

Нумерация пойдёт в таком порядке: 0/1, -1/1, 1/1, -2/1, -1/2, 1/2, 2/1-3/1, -2/2, -1/3, 1/3, 2/2, 3/1, -4/1, …………………

Нумерация объединения конечного множества счётных множеств

а11 а12 ….. а1n …..

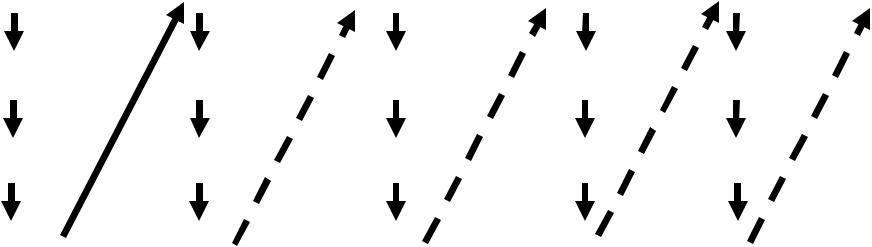
Множества занумерованы – от 1 до n. Нумерация объединения идёт по

показанной на рисунке схеме: сначала нумеруются первые элементы всех

множеств, начиная с множества № 1 и до множества № n, затем вторые …

Если объединяемые множества пересекаются, то повторяющиеся элементы пропускаются

Нумерация объединения счётного множества конечных множеств

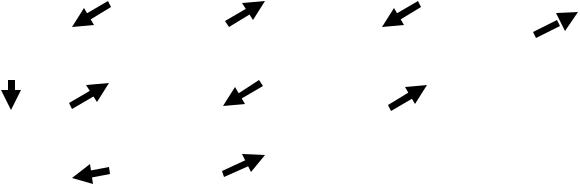
Множества занумерованы, начиная с № 1, элементы m-го множества имеют

номера с 1 до nm. Нумеруем сначала множество № 1, начиная с его первого

элемента, затем точно так же множество № 2 и т.д.

Если объединяемые множества пересекаются, то повторяющиеся элементы пропускаются

Нумерация объединения счётного множества счётных множеств

а11 а12 а13 а14 ….. а1n ….. …..

Множества также занумерованы, начиная с № 1 и т.д. Нумерация объединения идёт по показанной на рисунке схеме – диагональным методом

Если объединяемые множества пересекаются, то повторяющиеся элементы пропускаются

Cчётность множества алгебраических чисел

Алгебраическим числом называется действительное число, которое может быть корнем уравнения с целыми коэффициентами a0 + a1x + a2x2 + … + anxn = 0

Многочлену вида a0 + a1x + a2x2 + … + anxn ставится в соответствие целочисленный кортеж (a0, a1, a2, … , an )

Счётность множества (n+1)-местных кортежей – как Nn+1

Каждое уравнение a0 + a1x + a2x2 + … + anxn = 0 при заданном n имеет конечное множество решений

Счётность счётного множества конечных множеств – показана ранее

Обратили внимание на счётность следующих множеств:

Декартова степень множества натуральных чисел Nk для любых k=2,3,… Объединение конечного множества счётных множеств Объединение счётного множества конечных множеств Объединения счётного множества счётных множеств

Известные в математике счётные множества:

Рациональные числа Комплексные числа Алгебраические числа

Образная иллюстрация всех этих примеров - см. https://www.youtube.com/watch?v=c9muBk20NkY

А существуют ли бесконечные множества, не являющиеся счётными?

4) Континуальные множества

Th.1.4.7 (Теорема Кантора) Множество всех (любых) действительных чисел отрезка [0,1] не является счётным

Доказательство Th.1.4.7

Множество действительных чисел интервала [0,1] – это совокупность любых бесконечных дробей вида

0.b1b2b3...bk..., где b1, b2, b3, ..., bk, ... - цифры

Допустим противное: Множество действительных чисел интервала [0,1] счётное, то есть существует его нумерация.

Обозначим действительное число, соответствующее в этой нумерации номеру i, через 0.ai1ai2ai3…aik… и расположим действительные числа интервала [0,1] в порядке номеров.