
Лекция дискрет 11
.pdf
Пример доказательства
Ассоциативность
|
|
|
x1 & (x2 & x3) = (x1 & x2) & x3 |
|
|
|
(3.2.1) |
|
||||||||||||||
|
|
|
|
x1 (x2 x3) = (x1 x2) x3 |
|
|
|
|
|
|
|
|
||||||||||
|
|
2 |
1 |
|
3 |
4 |
|
|
|
|
|
6 |
5 |
|
7 |
8 |
|
|
||||
F1 = x&(y&z) = (x&y)&z = F2 |
|
|
F3 = x (y z) = (x y) z = F4 |
|||||||||||||||||||
x |
y z |
|
1 |
F1 |
|
|
|
3 |
F2 |
|
x |
y z |
5 |
F3 |
|
|
|
7 |
F4 |
|||
0 |
0 |
0 |
|
0 |
0 |
|
|
|
0 |
0 |
|
0 |
|
0 |
0 |
0 |
0 |
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
|
0 |
0 |
|
|
|
0 |
0 |
|
0 |
|
0 |
1 |
1 |
1 |
|
|
|
0 |
1 |
0 |
1 |
0 |
|
0 |
0 |
|
|
|
0 |
0 |
|
0 |
|
1 |
0 |
1 |
1 |
|
|
|
1 |
1 |
0 |
1 |
1 |
|
1 |
0 |
|
|
|
0 |
0 |
|
0 |
|
1 |
1 |
1 |
1 |
|
|
|
1 |
1 |
1 |
0 |
0 |
|
0 |
0 |
|
|
|
0 |
0 |
|
1 |
|
0 |
0 |
0 |
1 |
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
|
0 |
0 |
|
|
|
0 |
0 |
|
1 |
|
0 |
1 |
1 |
1 |
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
|
0 |
0 |
|
|
|
1 |
0 |
|
1 |
|
1 |
0 |
1 |
1 |
|
|
|
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
|
|
|
1 |
1 |
|
1 |
|
1 |
1 |
1 |
1 |
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

2) Булевы алгебры
Из § 2.1: Алгебра – множество М с заданной на нём совокупностью операций Ω = { φ1, φ2, … , φm, … }, т.е. структура
A = [ M; φ1, φ2, … , φm, … ]
Тип алгебры А – вектор арностей её операций
( ) Алгебра типа (2, 2, 1) называется булевой алгеброй, если её операции удовлетворяют соотношениям (3.2.1) – (3.2.10)
Из § 2.1: |
Структура B = [ B (M); , , |
|
] с булеаном B (M) в |
|
|
||||
|
||||
качестве носителя и операциями объединения, |
||||
|
||||
|
пересечения и дополнения множеств называется |
|||
|
булевой алгеброй множеств над множеством М |
|||

Является ли булева алгебра множеств, определённая в § 2.1, булевой алгеброй в смысле определения ( )?
|
Определение ( ) |
|
|||
|
|
|
|
||
|
Алгебра [B (M); , , |
] |
|||
|
Операция дизъюнкции |
Операция объединения |
|||
|
Операция конъюнкции & |
Операция пересечения |
|||
|
Операция отрицания |
Операция дополнения до М |
|||
|
Константа 0 |
Пустое множество |
|||
|
Константа 1 |
Множество М |
|||
|
|
|
|
|
|
|
|
|
|
|
|
Необходимо доказать соотношения вида (3.2.1) – (3.2.10) для операций булевой алгебры множеств [ B (M); , , ]
|
|
||||||
Свойства операций алгебры B = [ B (M); , , |
|
|
] |
||||
Ассоциативность |
|
|
|
|
|
|
|
M1 (M2 M3) = (M1 M2) M3 |
(3.2.1 ) |
||||||
|
|||||||
M1 (M2 M3) = (M1 M2) M3 |
|
||||||
Коммутативность |
|
|
|
|
|
(3.2.2 ) |
|
M1 M2 = M2 M1 |
M1 M2 = M2 M1 |
|
|||||
Дистрибутивность пересечения относительно объединения |
|||||||
M1 (M2 M3) = (M1 M2) (M1 M3 ) |
(3.2.3 ) |
||||||
Дистрибутивность объединения относительно пересечение |
|||||||
M1 (M2 M3) = (M1 M2) (M1 M3 ) |
(3.2.4 ) |
||||||
Идемпотентность |
Двойное дополнение |
||||||
M1 M1 = M1 M1 M1 |
= M1 (3.2.5 ) |
|
|
|
|
(3.2.6 ) |
|
|
|
|
|
|
|||
|
M1 = M1 |
||||||

|
|
|
|
|
|
|
|
|
|
|
Свойства констант |
|
|||||||||||
|
|
M1 M = M1 |
|
|
M1 = |
(3.2.7 ) |
|||||||||||||||||
|
|
M1 M = M |
|
|
M1 = M1 |
||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= M |
|
|
|
|
|
|
|
|
|
M = |
|
|||||||||
|
|
|
|
|
|
Правила де Моргана |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(M1 M2) = M1 M2 |
(M1 M2) = M1 M2 |
(3.2.8 ) |
|||||||||||||||||||||
|
Закон противоречия |
|
Закон исключённого третьего |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
M1 M1 |
= |
|
(3.2.9 ) |
|
|
M1 M1 = M |
(3.2.10 ) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
y |
|
|
|
z |
|
M1 M |
|
M2 M |
M3 M |
|||||||||
|
x & y |
|
|
M1 M2 |
|
|
|
|
|
0 |
|
|
|
||||||||||
|
x y |
|
|
M1 M2 |
|
|
|
|
|
1 |
|
|
M |
||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
M1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
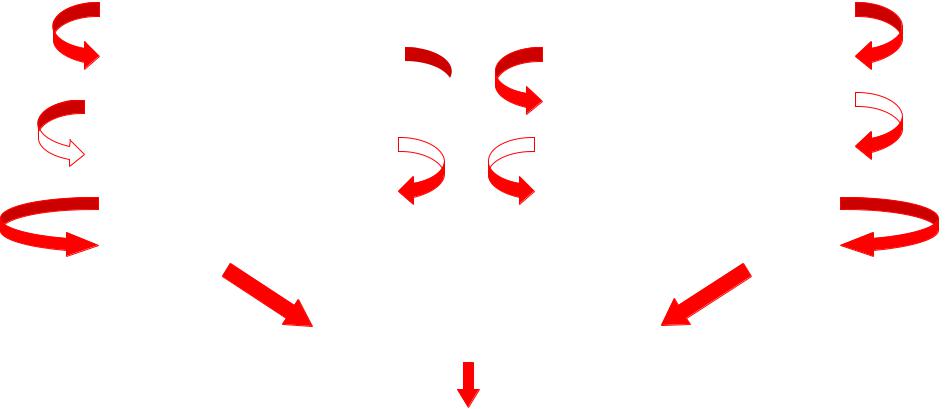
Ассоциативность |
|
|
M1 (M2 M3) = (M1 |
M2) M3 |
(3.2.1 ) |
x M1 (M2 M3) |
x (M1 M2) M3 |
|
x M1, x M2 M3 |
x M1 M2, x M3 |
|
x M1, x M2, x M3 
 x M1 M2, x M3
x M1 M2, x M3 
x (M1 M2) M3 M1(M2M3)(M1M2)M3
x M1, x M2, x M3
 x M1, x (M2 M3)
x M1, x (M2 M3)
x M1 (M2 M3) (M1M2)M3M1(M2M3)
M1(M2M3) (M1M2)M3 M1(M2M3)
M1 (M2 M3) = (M1 M2) M3

Булевы алгебры логических функций
[ P2; , &, ¬ ]
[ P2(n); , &, ¬ ]
Так как логические функции дают при вычислении 0 или 1, проверка соотношений (3.2.1) – (3.2.10) – таблицы истинности
Множество логических функций m переменных P2(n) замкнуто относительно операций , & и ¬ , так как их применение к функциям n переменных даёт в результате функции (не более чем) n переменных (с точностью до переименования переменных и введения и/или удаления фиктивных переменных)
[ P2(n); , &, ¬ ] - подалгебра [ P2; , &, ¬ ]
Булева алгебра двоичных векторов
Bn = { σ = (σ1, σ2, … , σn): σi {0, 1}, i=1…n } ¬σ = (¬σ1, ¬σ2, … , ¬σn)
σ τ = (σ1 τ1, σ2 τ2, … , σn τn) σ&τ = (σ1&τ1, σ2&τ2, … , σn&τn)
[ Bn; , &, ¬ ]
Операции над векторами σ и τ выполняются покоординатно, что обеспечивает выполнение соотношений (3.2.1) – (3.2.10)
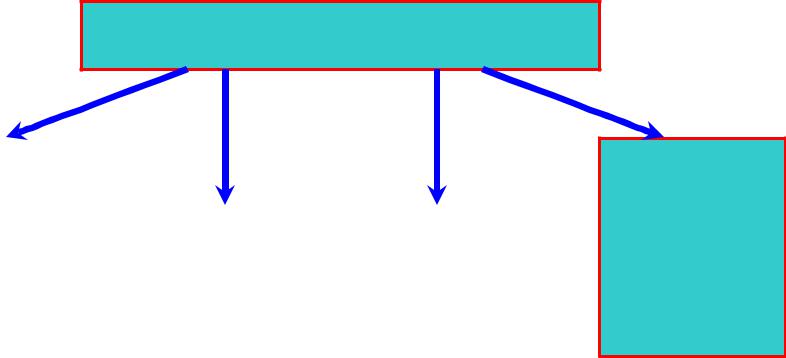
Булева алгебра
|
Булева |
|
|
|
|
||
|
|
Булева |
|
Булева |
|||
|
алгебра |
|
|
||||
|
|
алгебра |
|
алгебра |
|||
|
множеств |
|
|
||||
|
|
логических |
|
логических |
|||
|
|
|
|
|
|
||
|
[B(M); , , ] |
|
|
||||
|
|
функций |
|
функций |
|||
|
|
|
|
|
|
||
|
|
|
|
|
[ P ; , &, ¬ ] |
|
[P2(n); , &, ¬] |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Булева
алгебра
двоичных
векторов
[Bn; , &, ¬ ]

3) Изоморфизмы булевых алгебр
Из § 2.1:
Заданы две алгебры одинакового типа (l1, l2, … , lp) A = [ K; φ1, φ2, … , φp ] B = [ M; ψ1, ψ2, … , ψp ]
Гомоморфизм алгебры А в алгебру В – отображение Г: К М, удовлетворяющее условию
Г ( φi ( kj1, kj2, … , kjli ) ) = ψi ( Г(kj1), Г(kj2), … , Г(kjli) )
для всех i = 1…p и для любых kjr K
Изоморфизм алгебры А на алгебру В – взаимно однозначный гомоморфизм
