
- •1.Задачи ,приводящие к понятию производной:
- •2.Производная функции.Геометрический и механический смыслы производной.Производные основных элементарных функций.Производная сложной функции.
- •3.Дифференциал функции.Аналитический и геометрический смысл дифференциала
- •4.Первообразная функции. Неопределенный интеграл, его свойства. Таблица основных неопределенных интегралов.
- •5. Определенный интеграл. Формула Ньютона-Лейбница. Свойства определенного интеграла. Геометрический смысл определенного интеграла. Определенный интеграл.
- •7.Случайные события. Классическое и статистическое определения вероятности случайного события. Виды случайных событий
- •8.Основные теоремы теории вероятностей.Повторные независимые испытания. Формула Бернулли.Формула Пуассона.
- •9.Дискретные случайные величины.Закон распределения дискретной случайной величины.Основные числовые характеристики дискретнойслучайной величины и ее свойства.
- •10.Непрерывные случайные величины.Функция распределениянепрерывной случайной величины и ее свойства.
- •11.Плотность распределения вероятностей непрерывной случайной величины и ее свойства. Основные числовые характеристики непрерывной случайной величины.
- •12. Нормальный закон распределения. Вероятность попадения нормально распределенной случайнойвеличиныв заданный интервал.Правило трех сигм.
- •13. Статистическая совокупность .Генеральная и выборочная статистические совокупности. Статистический дискретный ряд распределения .Полигоны частот и относительных частот.
- •14.Статистический интервальный ряд распределения.Гистограммы частоти относительных частот.
- •15.Выборочные характеристики распределения.Точечные оценки основныхчисловых характеристик генеральной совокупности
- •16.Интервалтьные оценки числовых характеристик генеральной совокупности.Доверительный интервал,доверительная вероятность. Распределение Стьюдента.
- •17. Основные понятия и определения колебательных процессов. Механические колебания. Гармонические колебания. Незатухающие колебания.
- •18. Затухающие колебания. Вынужденные колебания. Резонанс. Автоколебания.
- •19. Механические (упругие) волны. Основные характеристики волн. Уравнение плоской волны. Поток энергии и интенсивность волны. Вектор Умова.
- •20. Внутреннее трение (вязкость жидкости). Формула Ньютона. Ньютоновские и неньютоновские жидкости. Ламинарное и турбулентное течение жидкости. Формула Гагена-Пуазейля.
- •21. Звук. Виды звуков. Физические характеристики звука. Характеристики слухового ощущения и их связь с физическими характеристиками звука. Шкала уровней интенсивности звука.
- •22. Закон Вебера-Фехнера. Шкала уровней громкости звука. Кривые равной громкости.
- •23. Ультразвук. Источники и приемники ультразвука, его основные свойства. Ультразвуковая эхолокация.
- •4. Действие ультразвука на вещество, клетки и ткани организма. Применение ультразвука в медицине.
- •25. Эффект Доплера и его использование в медико-биологических исследованиях
- •26. Законы отражения и преломления света. Явление полного внутреннего отражения. Предельный угол преломления. Предельный угол полного отражения.
- •27. Принцип действия рефрактометра. Ход лучей рефрактометра в проходящем и отраженном свете.
- •28. Биологические мембраны, их структура и функции. Модели мембран.
- •29. Перенос частиц через мембраны. Уравнение Фика. Применение уравнения Фика к биологической мембране. Уравнение Нернста-Планка.
- •30. Пассивный транспорт и его основные виды. Понятие об активном транспорте.
- •31. Биоэлектрические потенциалы. Потенциал покоя. Механизм генерации потенциала действия.
- •1Состояние покоя 2 началась деполяризация
- •3Участок полностью деполяризован 4началась реполяризация
- •32. Переменный ток. Полное сопротивление в цепи переменного тока. Импеданс тканей организма. Дисперсия импеданса.
- •33. Устройство простейшего оптического микроскопа. Разрешающая способность и предел разрешения микроскопа. Способы увеличения разрешающей способности микроскопа. Иммерсионные системы.
- •34. Полное и полезное увеличения микроскопа. Ход лучей в микроскопе. Апертурная диафрагма и апертурный угол.
- •35.Поглощение света. Закон Бугера. Закон Бугера-Ламберта-Бера. Конценрационная колориметрия.Нефелометрия.
- •36.Рассеяние света.Явление Тиндаля.Молекулярное рассеяние,Закон Рэлея.Комбинационное рассеяние.
- •37.Свет естественный и поляризованный.Поляризатор и анализатор. Закон Малюса
- •38.Поляризация света при отражении и преломлении на границе двух диэлектриков. Закон Брюстера.
- •39.Поляризация света при двойном лучепреломлении. Призма Николя. Вращение плоскости поляризации. Закон Био.
- •40.Тепловое Законы теплового излучения. Формула Планка.
- •1.Закон Кирхгофа: отношение излучательной способности тела к его поглощательной способности не зависит от природы тела и для всех тел является одной и той же функцией длины волны и температуры:
- •2. 2. Закон Стефана – Больцмана: полная (по всему спектру) излучательная способность абсолютно черного тела пропорциональна четвертой степени абсолютной температуры:
- •3. Закон Вина (закон смещения): длина волны на которую приходится максимум энергии излучения абсолютно черного тела обратно пропорциональна абсолютной температуре:
- •41.Излучение Солнца .Инфракрасное и ультрафиолетовое излучения и их применение в медицине.
- •42.Теплоотдача организма.Физические основы термографии.
- •43.Люминесценция, ее виды. Механизм и свойства люминесценции. Правило Стокса.
- •44.Применение люминофоров и люминесцентного анализа в медицине и фармации.
- •45.Вынужденное излучение. Инверсная заселенность уровней. Основные элементы лазера.
- •1.Устройство,поставляющее энергнию для переработки ее в когерентное излучение
- •2.Активная среда,которая вбирает в себя эту энергию и переизлучает ее в виде когерентного излучения
- •3.Устройство ,осуществляющее обратную связь
- •49.Первичные процессы взаимодействия рентгеновского излучения веществом: когерентное рассеяние, комптон-эффект, фотоэффект.
- •50.Физические основы применения рентгеновского излучение в медицине. Рентгенодиагностика. Современные рентгеновские компьютерные томографы.
- •51.Явление радиоактивности. Виды радиоактивного распада. Основной закон радиоактивного распада.
- •52. Альфа-распад ядер и его особенности. Бета-распад, его виды, особенности и спектр. Гамма излучение ядер.
- •53.Взаимодействие ионизирующего излучения с веществом
- •54.Методы радиационной медицины. Радионуклидная диагностика.
- •55.Методы радиоизотопной терапии.
- •56.Ускорители заряженных частиц и их использование в медицине.
- •57. Дозиметрия ионизирующего излучения. Поглощенная и экспозиционная дозы. Мощность дозы.
- •58. Количественная оценка биологического действия ионизирующего излучения. Коэффициент качества излучения. Эквивалентная доза.
- •59. Первичное действие ионизирующих излучений на организм. Защита от ионизирующих излучений.
- •60. Лучевая болезнь, ее виды. Периоды и симптомы острой лучевой болезни.
1.Задачи ,приводящие к понятию производной:
а)о скорости движения материальной точки
б) об угле наклона касательной к графику функции
А.Пусть
некоторая материальная точка совершает
прямолинейное движение. В момент времени
t1
точка находится в положении М1. В момент
времени t2
в положении М2. Обозначим промежуток
М1,М2 через ΔS
; t2-t1=Δt
. Величина ΔS/Δt
называется средней скоростью движения.
Чтобы найти мгновенную скорость точки
в положении М1 необходимо Δt
устремить к нулю. Математически это
значит, что: VM1=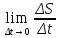 ,
таким образом , для нахождения мгновенной
скорости материальной точки необходимо
вычислить предел отношения приращения
функции ΔS
к приращению аргумента Δt
при условии ,что Δt
→0.
,
таким образом , для нахождения мгновенной
скорости материальной точки необходимо
вычислить предел отношения приращения
функции ΔS
к приращению аргумента Δt
при условии ,что Δt
→0.

Б.График:
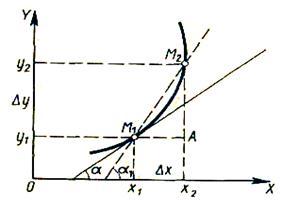
Рассмотрим
график некоторой функции y=f(x).
В точке М1 проведем касательную к графику
функции. На графике выберем производную
М2 и проведем секущую . Она наклонена к
оси ОХ под углом α1. Рассмотрим ΔM1M2A:
tgα1=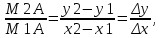 Если точку М1 фиксировать, а точку М2
приближать к М1 , то секущая М1М2 будет
переходить в касательную к графику
функции в точке М1 и можно записать:tgα=
Если точку М1 фиксировать, а точку М2
приближать к М1 , то секущая М1М2 будет
переходить в касательную к графику
функции в точке М1 и можно записать:tgα=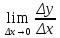 .Предел отношения
приращения △у
функции у=f(x) к приращению аргумента △x
в заданной точке х0 при стремлении △х
к нулю, называется производной функции
в заданной точке. Обозначения производной:
y’,f’(x),
.Предел отношения
приращения △у
функции у=f(x) к приращению аргумента △x
в заданной точке х0 при стремлении △х
к нулю, называется производной функции
в заданной точке. Обозначения производной:
y’,f’(x), По определениюy’=
По определениюy’=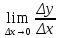 ,
где Δх=х2-х1-приращение аргумента,
Δу=у2-у1-приращение функции.
,
где Δх=х2-х1-приращение аргумента,
Δу=у2-у1-приращение функции.
2.Производная функции.Геометрический и механический смыслы производной.Производные основных элементарных функций.Производная сложной функции.
Предел отношения приращения △у ФУНКЦИИ У=f(x) к приращению аргумента △x в заданной точке х0 при стремлении △х к нулю, называется производной функции в заданной точке . Обозначения производной : ______________________________
_______________________________________________ ,где
Нахождения производной функции называется дифференцированием.Дифференциирование основных элементарных функций проводится по формулам и правилам :
1,(u+v+w) '=u '+v '+w '
2. (u v)=u '+v '+w '
3.
Геометрический смысл производной.
Величину тангенса угла наклона касательной ,проведенной к графику функции,в математике называют угловым коэффицентом касательной . Угловой коэффицент касательной ,проведенной к графику дифференцируемой функции в некоторой точке ,численно равен производной функции в данной точке
Механический
смысл производной. Рассмотрим
простейший случай: движение материальной
точки вдоль координатной оси, причём
закон движения задан: координата x
движущейся точки – известная
функция x ( t )
времени t.
В течение
интервала времени от t0
до t0 + ![]() точка
перемещается на расстояние: x ( t0 +
точка
перемещается на расстояние: x ( t0 + ![]() ) - x ( t0 )
=
) - x ( t0 )
= ![]() ,
а её средняя
скорость равна: va =
,
а её средняя
скорость равна: va = ![]() /
/ ![]() . При
. При ![]()
![]() 0
значение средней скорости стремится к
определённой величине, которая
называется мгновенной
скоростью v ( t0 )
материальной точки в момент времени t0 .
Но по определению производной мы имеем:
0
значение средней скорости стремится к
определённой величине, которая
называется мгновенной
скоростью v ( t0 )
материальной точки в момент времени t0 .
Но по определению производной мы имеем:
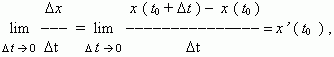
отсюда, v ( t0 ) = x’ ( t0 ) , т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной.Аналогично, ускорение – это производная скорости повремени: a = v’ ( t ).

Производная сложной функции .Из элементарных функций образуются сложные функции .Например ,задана функция y=f(u),где u в свою очередб зависит от х , т.е u=φ(x). Тогда,при изменении х будут меняться u и y .В этом члучае заданная функция y=f(u) называется СЛОЖНОЙ и обозначается y=f{ φ(x)}.Величина u называется ПРОМЕЖУТОЧНОЙ ПЕРЕМЕННОЙ .тогда : y ' =y ' u * u ' x
