Методические рекомендации к решению типовой задачи по теме

Сила вариации (изменчивость, колебания) значений признаков количественно оцениваются с помощью показателей вариации:

1. размах вариации ;

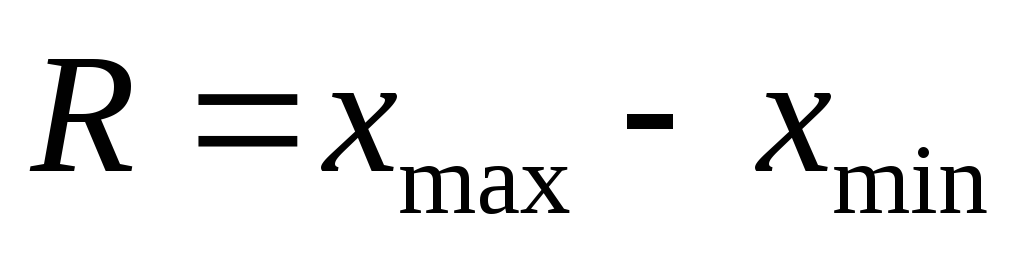2. среднее линейное отклонение:

а) простое (по несгруппированным данным) ;

б) взвешенное (по сгруппированным данным) ;

3. среднее квадратическое отклонение (степенная средняя второй степени из индивидуальных отклонений):

а) простое ;

б) взвешенное :

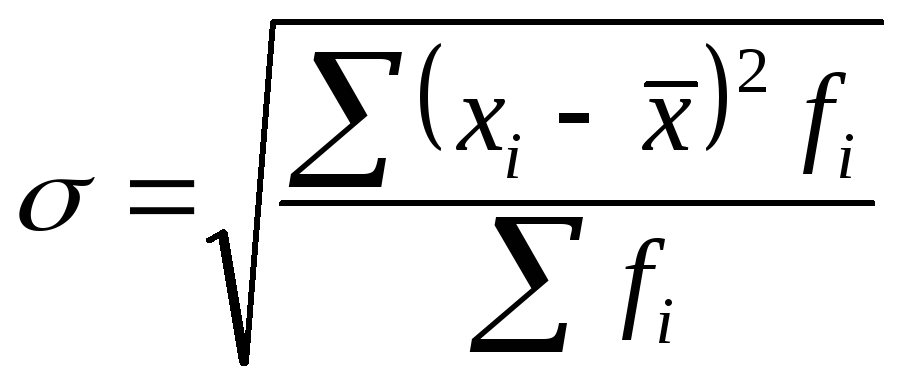4. дисперсия Д = ², или иным способом: Д =, где

или .

Общая дисперсия состоит из межгрупповой и средней из групповых дисперсий. Все виды дисперсий широко применяются для дисперсионного анализа аналитических группировок, оценки ошибок выборочного обследования и т. д. Студент должен усвоить порядок вычисления общей, межгрупповой и средней из групповых дисперсий и знать случаи их применения.

5. для оценки типичности средней используют среднеквадратический коэффициент вариации (V):

Если, то совокупность считается однородной, а средняя – типичной.

Пример. Исследование фирм по объемам годовой товарной продукции дало следующие результаты:

Группы фирм по объему продукции, тыс. грн	Количество фирм в группе, ед
До 100	6
100–150	27
150–200	2

Определите показатели вариации продукции. Сделайте вывод об однородности совокупности и типичности среднего значения продукции для данных фирм.

Решение:

Для расчетов рекомендуется оформить расчетную (вспомогательную) таблицу:

Группы фирм по объему продукции, тыс.  грн (интервалы)	Количе ство фирм в группе, ед. ()	Середина интервала ()
50–100	6	75	450	-44,3	1 962,5	11 774,9
100–150	27	125	3 375	5,7	32,5	877,2
150–200	2	175	350	55,7	3 102,5	6 205,0
Итого	35	–	4 175	–		18 857,1

1. определяем средний объем продукции одной фирмы:

;

2. определяем дисперсию:

;

3. находим среднеквадратическое отклонение:

;

4. находим коэффициент вариации:

.

Поскольку V < 33,3%, то совокупность считается однородной, а средняя – типичной.

Задачи и задания для выполнения на практических занятиях и домашних работ

5.1. По известным данным о возрасте рабочих двух молодежных бригад определите отдельно для каждой бригады модальное число лет, медиану, первый и третий квартили из приведенных рядов распределения:

Возраст, лет	Количество рабочих, чел.
	бригада № 1	бригада № 2
18	20	–
18,5	35	10
19	19	15
19,5	16	20
20	4	36
20,5	1	14
Итого	95	95

5.2. Опрос потребителей о приемлемой для них цене на новый товар дал следующие результаты:

Цена товара, грн	10–12	12–14	14–16
Доля потребителей, признающих цену приемлемой, % к опрошенным	45	30	25

Определите: 1) среднюю приемлемую цену на данный товар; 2) все известные вам показатели вариации (размах вариации, среднее линейное отклонение, дисперсию, среднеквадратическое отклонение); 3) среднеквадратический коэффициент вариации. Сделайте вывод об однородности совокупности и типичности средней.

5.3. Распределение семей по уровню среднедушевого денежного дохода характеризуется такими данными за месяц:

Группы семей по уровню дохода на одного человека в месяц, условных денежных ед.	Число семей, % к итогу
	городских	сельских
До 30,0	9,2	22,8
30,1–60,0	18,5	38,7
60,1 – 90,0	39,1	26,5
90,1 – 120,0	17,0	7,9
Более 120,0	16,2	4,1

Определите: 1) коэффициенты вариации уровня среднедушевого денежного дохода по отдельным категориям семей; 2) сравните вариацию доходов городских и сельских семей. Найдите моду и медиану распределения.

5.4. Известны следующие данные о распределении фирм по числу работников:

Группы фирм по числу работников, чел.	Количество фирм
До 30	5
30–50	9
50–70	18
70–90	41
90–110	36
110–130	24
130 и более	8
Итого	141

Рассчитайте: 1) среднюю численность работников; 2) показатели вариации (средние линейное и квадратическое отклонения, дисперсию, коэффициент вариации); 3) моду, медиану, квартили и крайние децили. Сделайте вывод об однородности совокупности и типичности средней.