Т е м а 5. Пересечение поверхностей

Цель – применить знания о построении в ортогональных проекциях линий пересечения поверхностей.

Линия пересечения кривых поверхностей может быть плоской и пространственной. Возможны четыре случая взаимного пересечения:

1.Частичное врезание, когда часть образующих одной поверхности пересекается частью образующих другой. Линия пересечения – замкнутая пространственная кривая (рис. 19).

2.Полное проникание: все образующие одной поверхности пересекаются со второй поверхностью. Линии пересечения распадаются на две (или больше) отдельные кривые (рис. 20).

х

3.Одностороннее внутреннее соприкосновение: пересекающиеся поверхности имеют в одной точке общую плоскость касания (рис. 21). Эта точка на кривой пересечения является или угловой (точка излома), или узловой (двойной).

4.Двойное соприкосновение: пересекающиеся поверхности имеют в двух точках общие касательные плоскости. В этом случае в пересечении участвуют все образующие обеих поверхностей и они пересекаются по двум кривым линиям (рис. 22).

37

Следует иметь в виду, что линия пересечения двух поверхностей в проекциях всегда располагается в пределах контура наложения проекций двух пересекающихся поверхностей (рис. 23).

нии получаются образующие; 4) пересечение тора и цилиндра, если последний лежит в плоскости, перпендикулярной оси

вращения тора.

Рассмотрим пример (рис. 24). Для построения линии пересечения сферы с конусом в качестве посредников выберем плоскости, параллельные плоскости π1 , – горизонтальные плоскости. В

этом случае обе поверхности будут рассекаться по окружностям, построить проекции которых и найти их точки пересечения весьма просто.

Рис. 24

38

Если в качестве посредников брать фронтальные или профильные плоскости, то на конусе придется строить гиперболы, что достаточно трудоемко и приводит к потере точности. Экстремальными будут точки A и B , фронтальные проекции которых принадлежат очеркам поверхностей. При рассечении поверхностей плоскостью ξ находим точки M и N . Точность построения

линии пересечения определяется количеством посредников.

Использовать семейство параллельных плоскостей можно и в том случае, когда вспомогательная плоскость пересекает одну из поверхностей вращения по эллипсам. Для этого следует преобразовать чертеж так, чтобы эллипсы, получающиеся в сечении, проецировались на вспомогательную плоскость в окружности. Рассмотрим построение линии пересечения эллиптического конуса и кругового цилиндра (рис. 25). В качестве посредников выберем плоскости, параллельные основанию конуса. Они будут рассекать цилиндр по образующим, а конус – по подобным эллипсам. Произведем замену плоскостей так, чтобы эллипсы проецировались на новую плоскость в окружности. Как выставить новую горизонтальную плоскость проекций? Для определения потребного направления проецирования используем эллипс верхнего основания конуса. Из фронтальной проекции центра проведем окружность радиусом, равным малой полуоси. Касательная к этой окружности, проведенная из фронтальной проекции точки L , и даст искомое направление, а значит, и расположение новой горизонтальной плоскости проекций. Проведем се-

кущую плоскость ω. Проекцией сечения конуса на плоскость π4 будет окружность. Цилиндр

рассечется по образующим, которые в системе x π2 будут фронталями. Точки пересечения го-

π4

ризонтальных проекций этих фронталей с окружностью и определят точки, принадлежащие линии пересечения заданных поверхностей. Описанная операция повторяется столько раз, сколько необходимо для обеспечения потребной точности построения линии пересечения.

Рис. 25

С помощью пучка плоскостей (вращающейся плоскости) можно решить следующие задачи:

1)построение линии пересечения двух произвольно расположенных конусов второго порядка. Осью пучка является прямая, проходящая через вершины конусов;

2)пересечение конуса и цилиндра. Осью пучка является прямая, проходящая через вершину конуса параллельно оси цилиндра.

Рассмотрим пример на построение линии пересечения двух конических поверхностей

(рис. 26).

Ось вращения вспомогательных плоскостей определим как линию a , соединяющую вершины конусов. Найдем горизонтальный след этой прямой Ha . Любая вспомогательная плоскость теперь будет определяться двумя пересекающимися прямыми: осью вращения и горизонтальным следом

– прямой, лежащей в плоскости π1 и проходящей через точку Ha . Секущая плоскость γ1 рассечет конус с вершиной S2 по образующим (так как проходит через вершину конусов) S23 и S2 2 и

39

будет касательной по отношению к конусус вершиной S1 . Линии касания – S11. Точки пересечения указанных образующих и дадут точки, принадлежащие линии пересечения конусов.

Рис. 26

Описанная операция повторяется многократно. Диапазон использования посредников определяется плоскостями касания к одной и другой поверхностям – γ1 и γ2 . Точки видимости –

точки пересечения очерковых образующих одного конуса с поверхностью другого. Вспомогательные сферы могут быть использованы в случае, если обе поверхности являются

поверхностями вращения и их оси пересекаются – поверхности имеют общую плоскость симметрии. Сфера пересекается с соосной поверхностью вращения по окружности, плоскость которой является проецирующей и на одной из плоскостей проекций отражается в прямую (рис. 27), что позволяет легко находить общие точки двух поверхностей вращения. При указанных выше условиях применяют концентрические сферы с центром в точке пересечения осей заданных поверхностей. Диапазон изменения радиуса посредника выбирается из следующих соображений.

Наибольший радиус сферы Rmax равен расстоянию до наиболее удаленной точки пересечения

очерков заданных поверхностей. Радиус наименьшей вспомогательной сферы равен радиусу большей из двух сфер, которые можно вписать в пересекающиеся поверхности.

Рис. 27

Рассмотрим пример (рис. 28). Впишем сферу в вертикально стоящую поверхность вращения. Линия касания – окружность, параллельная плоскости π1 . Ее фронтальная – прямая линия. Эта

сфера Rmin рассечет наклонный цилиндр по окружности, фронтальная проекция которой тоже прямая линия. Общая точка – C . Сфера максимального радиуса Rmax =O′′A′′. Нахождение про-

40

межуточных точек с использованием сфер Rmin ≤ R ≤ Rmax ясно из чертежа. Точки A и B являются точками видимости на π2 . На фронтальной плоскости проекций видимая и невидимая час-

ти линии пересечения сливаются. Видимость на горизонтальной плоскости проекций определяется точками пересечения очерковых образующих цилиндра с поверхностью вращения (E ).

Рис. 28

Если одна из поверхностей является поверхностью вращения, а вторая имеет семейство круговых сечений, причем обе поверхности имеют общую плоскость симметрии, на которую круговые сечения второй поверхности проецируются в виде прямых линий, то для построения линии пересечения используются эксцентричные сферы. Принцип определения центра вспомогательной сферы можно проследить на рис. 29. Центрами вспомогательных сфер будут точки пересечения оси вращения первой поверхности с перпендикулярами, восстановленными в центре произвольно выбранного кругового сечения второй поверхности. Радиус сферы равен радиусу окружности, проходящей через концы отрезка, – проекции кругового сечения.

С помощью эксцентрических сфер можно решать следующие задачи на пересечение поверхностей:

1) поверхности вращения и кругового тора, если ось первой лежит в плоскости симметрии тора, перпендику- Рис. 29 лярной его оси вращения;

41

2)сферы с поверхностью второго порядка, имеющей круговые сечения, если плоскость симметрии этой поверхности, на которую круговые сечения проецируются в виде прямых линий, является меридиональной плоскостью сферы;

3)поверхности вращения и эллиптического цилиндра или конуса, если заданные поверхно-

сти имеют общую плоскость симметрии и круговые сечения эллиптического цилиндра или конуса на эту плоскость проецируются в виде прямых линий.

Пример решения приведен на рис. 30.

Рис. 30

Строим линию пересечения конуса с тором. Выберем на торовой поверхности окружность. Для этого проведем через ось тора фронтально-проецирующую плоскость ω. Выбранная ок-

ружность на фронтальной плоскости проекций будет представлена отрезком A′′B′′. Найдем центр и радиус вспомогательной сферы, которая будет рассекать тор по этой окружности так,

чтобы центр лежал на оси конуса. Проведем через середину отрезка A′′B′′ перпендикуляр до пересечения с осью конуса. Сфера, проведенная чрез точку O , рассечет торовую поверхность по

выбранной нами окружности, конус – по окружности, параллельной плоскости π1 (фронтальная

проекция C′′D′′). Общая для них точка M принадлежит искомой линии пересечения. Указанная операция повторяется исходя из требований к точности построений.

Вспомогательные секущие сферы могут использоваться для построения линий перехода в корпусах промышленных изделий, получаемых литьем. Это нужно не только для построения проекционных моделей, но и для изготовления форм и моделей для процесса отливки. На рис. 31 показано использование способа концентрических сфер на чертеже вентиля для построения фронтальной проекции линии пересечения цилиндра Φ с тором Ω. Центром вспомогательных сфер будет точка пересечения осей. Радиус вспомогательных сфер лежит в диапазоне

O′′M ′′≤ Rb < O′′N′′.

Сфера радиусом O′′P′′ рассечет цилиндр и тор по окружностям, фронтальные проекции которых – отрезки L′′K′′ и M ′′P′′. Общая точка T′′ – вершина искомой кривой. Еще две точки найдем с помощью сферы радиусом Rb1.

На рис. 32 показано построение проекций линии перехода корпуса для наружной и внутренней поверхностей способом эксцентрических сфер.

42

Рис. 31

Рис. 32

В случае, когда одна из пересекающихся поверхностей является проецирующей, отпадает необходимость использования посредников, так как можно использовать условие принадлежности. На рис. 33 показано построение линии пересечения сферы с цилиндром. Особенностями данной задачи является проецирующее положение цилиндрической поверхности и одностороннее внутреннее соприкосновение поверхностей. Узловая точка линии пересечения – точка соприкосновения 1 – лежит в плоскости симметрии на главном меридиане сферы. Фронтальная проекция цилиндра совпадает с фронтальной проекцией искомой линии пересечения.

Следовательно, задачу можно сформулировать так: задана фронтальная проекция линии пересечения двух тел. Найти ее горизонтальную и профильную проекции. Принцип решения покажем на примере точки K . Так как эта точка принадлежит обеим поверхностям, то она лежит и на поверхности сферы. Радиус параллели, на которой она лежит, равен расстоянию от оси до T′′. Про-

водим горизонтальную проекцию этой окружности и находим на ней K′. Дальше действуем аналогично. Точки 2,8,4,10 являются точками видимости на соответствующих плоскостях проекции.

43

Рис. 33

На рис. 34 представлена задача на пересечение тора с цилиндром, когда также имеет место случай одностороннего внутреннего соприкосновения, но точка соприкосновения, в отличие от рассмотренного ранее примера, является угловой или точкой излома. Так как цилиндр горизон- тально-проецирующий, то решение сводится к нахождению фронтальных и профильных проекций точек, лежащих на торовой поверхности (на параллелях тора). Суть построения ясна из рисунка. Угловая точка лежит на экваторе торовой поверхности.

Рис. 34

44

Линия пересечения поверхностей второго порядка есть алгебраическая кривая четвертого порядка. На практике используют ситуации, в которых кривая четвертого порядка распадается на более простые кривые низших порядков (например, на четыре прямые при пересечении двух цилиндров – рис. 35).

Весьма важным является случай распадания кривой четвертого порядка на две плоские кривые второго порядка. Признаки такого распадания сформулированы в следующих теоремах.

1.Если две поверхности второго порядка пересекаются по одной плоской кривой, то они пересекаются и еще по одной кривой, которая тоже будет плоской (рис. 36).

2.Если две поверхности второго порядка имеют две точки соприкосновения, то линия их пересечения распадается на пару кривых второго, плоскости которых проходят через прямую, соединяющую точки соприкосновения (рис. 36). Эта теорема называется теоремой о двойном соприкосновении.

Пример решения задачи с использованием теоремы о двойном соприкосновении приведен на рис. 37. Нужно построить линию пересечения полуцилиндра с конусом. Точки соприкосновения – 3. Знание теоремы позволяет при решении задачи не использовать посредников. Строим фронтальную проекцию линии пересечения – два эллипса, проходящих через точки соприкосновения и точки пересечения образующих цилиндра и конуса. Горизонтальную проекцию строим из условия принадлежности. Точка 2 лежит на поверхности цилиндра. Значит, она лежит на об-

разующей (прямой линии), находящейся на расстоянии Y2 от плоскости симметрии. На горизонтальной проекции этой образующей лежит горизонтальная проекция точки 2.

Рис. 37

45

3.Если две поверхности второго порядка имеют общую плоскость симметрии, то линия их пересечения проецируется на эту плоскость в виде кривой второго порядка.

4.Теорема Монжа. Если две поверхности второго порядка описаны около третьей или вписаны в нее, то они пересекаются по двум плоским кривым, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания. На рис. 38, 39 представлены примеры построения линии пересечения поверхностей I и II , описанных около или вписанных в поверхность III .

Рис. 38 Рис. 39

Доказательство теоремы Монжа основано на использовании теоремы о двойном соприкосновении. Обратимся к рис. 38, где показаны две конические поверхности. Очевидно, что поверхности I и III , так же как и поверхности II и III , соприкасаются по плоским кривым, лежащим на поверхности III . Эти линии пересекаются в двух точках. Касательные плоскости, построенные в этих точках, будут касательными к обеим поверхностям. Таким образом, обе поверхности имеют двойное соприкосновение в данных точках и на основании теоремы о двойном соприкосновении пересекаются по плоским кривым, проходящим через прямую, соединяющую точки соприкосновения.

На рис. 40 приведены часто встречающиеся на практике варианты пересечения цилиндров и конусов вращения, описанных около сферы.

Рис. 40

46

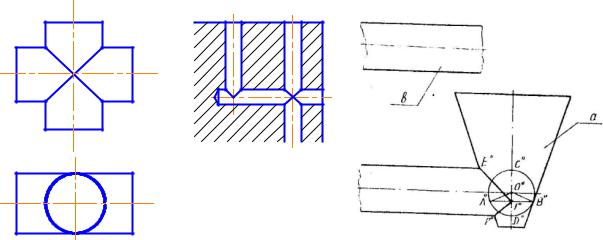
Примером практического применения теоремы Монжа может служить конструирование трубопроводов из листового материала, моделей для отливки фитингов, построение линий пересечения отверстий одинакового диаметра (рис. 41) и т.д.

Пусть требуется соединить коническую емкость a с цилиндрическим трубопроводом b под прямым углом (рис. 42). Причем расстояние от трубы до днища емкости можно менять в довольно широком диапазоне. В этом случае можно построить линию пересечения поверхностей для фиксированного расстояния, нанести ее на обе поверхности, осуществить обработку по этим линиям и произвести сварку.

Технологический процесс обработки в таком варианте будет сложным и трудоемким. Проще было бы резать обе поверхности по проецирующим плоскостям. При использовании теоремы Монжа это возможно. Подберем точку пересечения осей конуса и цилиндра (O ) так, чтобы она являлась центром сферы, около которой описаны заданные геометрические тела. Окружность касания конуса и сферы на фронтальной плоскости спроецируется как отрезок A′′B′′, а окружность касания цилиндра и сферы – как C′′D′′. Точка пересечения линий касания – 1''. Соединяем точки E′′ и F′′ с точкой 1'' и получаем фронтальную проекцию искомой линии пересечения.

Задачи на построение линий пересечения поверхностей условно можно разбить на три группы:

1)технологические – построение линий пересечения элементов деталей, образующихся в процессе изготовления и обработке;

2)конструкторские – построение линий пересечения элементов конструкций, например в производстве летательных аппаратов (крыла и мотогондолы, корпуса и сопла), в строительстве и архитектуре (элементов кровли, всевозможных оболочек);

3)задачи, которые возникают при проведении научных исследований, например в области газовой динамики.

Рассмотрим задачу о построении линий пересечения газовых струй, линий пересечения поверхности струи с конструкцией, в области радиолокации и т.п.

П р и м е р 1. Построить горизонтальную проекцию выемки, которая образуется на неподвижной цилиндрической детали при обработке вращающейся конической фрезой, перемещаю-

щейся в направлении от точки O1 до точки O2 (рис. 43).

Анализ данных. Поверхность детали фронтально-проецирующая, фреза перемещается параллельно горизонтальной плоскости проекций.

Анализ решения. При обработке вращающейся фрезой, перемещающейся параллельно плоскости проекции, на детали образуется линия, соответствующая линии сечения детали плоскостью, угол наклона которой к плоскостям проекций определяется через угол конусности фрезы. Следовательно, задача распадается на две части: нахождение линии сечения плоскостью на участке движения фрезы и нахождение линии пересечения цилиндра с конусом в конечном положении фрезы. Обе части решаются введением вспомогательных секущих поверхностей, в качестве которых удобно выбрать плоскости, параллельные горизонтальной плоскости проекций. При их введении на поверхности цилиндра легко найти образующие, по которым он рассекается

47

этими плоскостями, а на поверхности фрезы – окружности и их траектории при поступательном движении. Линии, принадлежащие одной секущей плоскости, пересекаются, образуя точки контура искомой выемки.

Алгоритм решения.

1.Вводим вспомогательные секущие плоскости γi , которые рассекают конус по окружности mi , а цилиндр по образующим Ki .

2.Находим mi =α∩γi ; Ki =β∩γi .

3.Проводим траектории движения окружности mi .

4.Находим точки пересечения траекторий с соответствующими образующими цилиндра. Соединяем горизонтальные проекции этих точек до момента прекращения поступательного движения фрезы.

5.Определяя точки пересечения образующих с окружностями при нахождении фрезы в точ-

ке O2 , достраиваем проекции выемки.

П р и м е р 2. Построить фронтальную проекцию линии пересечения конической и торовой оболочек, имеющих общую плоскость симметрии, параллельную V (рис. 44).

Анализ данных. Оси поверхностей не пересекаются, i1 π2 ; i2 π1 . Поверхности имеют общую плоскость симметрии, параллельную π2 .

Анализ решения. Анализ данных говорит о том, что есть предпосылки для использования метода вспомогательных сфер. Если через любое круговое сечение поверхности одной оболочки можно провести сферу, пересекающую другую оболочку также по окружности, то можно применить для решения метод эксцентрических сфер. При решении другими способами пришлось бы строить лекальные кривые.

Алгоритм решения.

1.Пересекаем торовую поверхность фронтально-проецирующей плоскостью γ1 , проходящей через ось тора. Линия пересечения – окружность, которая проецируется на π 2 в отрезок (1'', 2'').

2.Из середины отрезка (1'', 2'') – точки K1′′ восставляем перпендикуляр к плоскости окружности (1,2) и отмечаем точку O1′′ его пересечения с осью конической оболочки.

3.Из точки O1′′ проводим сферу радиусом, равным отрезку O1′′ I′′. Эта сфера пересечет торовую поверхность по окружности 1,2, а коническую – по окружности 3,4, фронтальная проекция которой – отрезок 3′′- 4′′.

48

чением очерковых образующих поверхностей.

0"3

Рис. 44

Варианты задания № 5

Варианты 1–10. Фреза, вращаясь вокруг оси, перемещается в направлении b . Ее конечное положение определяется точкой O2 . Построить проекции выемки, получаемой при обработке

фрезой подвижной детали.

Варианты 11–13. Построить на чертеже проекции границы зоны набольших силовых и тепловых нагрузок на корпус летательного аппарата при работе реактивного двигателя (линия пересечения поверхности струи с корпусом). Сопло – круговой конус. Поверхность струи – поверхность вращения, фронтальный очерк которой изображен на чертеже.

Варианты 14–19. Изобразить на чертеже горизонтальную и фронтальную проекции крышки сопла реактивного двигателя – части цилиндрической поверхности корпуса, ограниченной линией пересечения сопла с поверхностью корпуса. Сопло – круговой конус с углом при вершине β. Угол между осью цилиндрического корпуса и осью сопла α . Толщиной материала пренебречь.

Вариант 20. Построить фронтальную проекцию вырезов на корпусе громкоговорителя (линия пересечения конической поверхности и цилиндрической горизонтально-проецирующей поверхности). Изобразить только видимые части вырезов.

Варианты 21–22. Построить фронтальную проекцию рукоятки.

Варианты 23–24. Построить линии пересечения на корпусе электропневмоклапана.

49