Т е м а 3. Преобразование чертежа

Цель – закрепить знания о методах преобразования чертежа.

Решение многих задач способами начертательной геометрии в конечном счете сводится к определению позиционных и метрических характеристик геометрических фигур. В связи с этим задачи можно условно разделить на позиционные, решение которых дает ответ на вопрос о взаимном расположении геометрических фигур по отношению друг к другу и относительно плоскостей проекций, и метрические, решение которых позволяет определить расстояния и углы между элементами одной или нескольких фигур.

Трудоемкость графического решения задачи часто зависит не от ее сложности, а от того, какое положение по отношению к плоскостям проекций занимают геометрические фигуры, входящие в исходные данные, т.е. проекции могут быть «удобными» и «неудобными» для решения. Начертательная геометрия располагает большим количеством методов преобразования «неудобных» для решения ортогональных проекций в «удобные». Наибольшее распространение нашли методы, основу которых составляет изменение взаимного расположения плоскостей проекций и проецирующей фигуры за счет ее перевода в частное положение. Такое преобразование может быть осуществлено двумя путями:

1)переходом от заданной системы плоскостей проекций к новой, по отношению к которой данная геометрическая фигура, при этом не меняющая своего положения в пространстве, займет частное положение;

2)перемещением в пространстве заданной геометрической фигуры в частное положение. Плоскости проекций при этом остаются неизменными.

Для решения задачи следует вспомнить суть основных классических способов преобразования проекций.

1. Замена плоскостей проекций. Получение новых, более удобных проекций достигается за счет перехода от заданных плоскостей проекций к новым. Положение новых плоскостей проекций следует выбирать так, чтобы по отношению к ним проецируемая геометрическая фигура за-

Замена одновременно только одной плоскости проекции обеспечивает неизменность одной плоскости, которая выполняет функции связующего звена между новой и исходной проекциями.

2. Метод плоскопараллельного перемещения. Перемещению подвергается геометрическая фигура, а плоскости проекций при этом остаются без изменения. Закон движения состоит в том, что все точки фигуры перемещаются по траекториям, расположенным в параллельных плоскостях. Траекториями движения могут служить и окружности, центры которых принадлежат одной прямой – оси вращения. Это частный случай метода плоскопараллельного перемещения, который называется способом вращения. В зависимости от расположения оси вращения различают способы вращения вокруг оси, перпендикулярной и параллельной плоскости проекций (вращение вокруг линии уровня).

Методы преобразования чертежа широко используются при решении прикладных задач. Почти во всех следующих заданиях потребуется использование преобразований. Здесь мы упомянем об их применении в машиностроении при построении на чертеже истинных величин сечений и поверхностей элементов деталей, при изображении на чертеже промежуточных положе-

19

ний элементов конструкций, определении отклонения осей деталей и узлов станка и т.п. При решении инженерных задач, связанных с векторами (теоретическая механика, теория механизмов и машин, сопротивление материалов), которые занимают общее положение относительно плоскостей проекций, также удобно пользоваться способами преобразования чертежа.

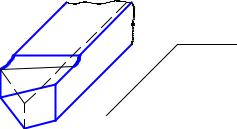
Одной из важных областей применения начертательной геометрии является проектирование и вычерчивание режущего инструмента. Токарный

жа. Эти углы необходимо знать для заточки резца на специальном станке.

Прежде чем рассмотреть несколько примеров, обратим внимание на то, когда целесообразно применять тот или иной способ преобразования. При использовании способа вращения следует иметь в виду, что вращение вокруг осей, перпендикулярных плоскостям проекций, в большинстве случаев приводит к запутанным построениям. Это часто происходит из-за наложения новых проекций на старые. Избежать наложения можно, применив способ параллельного перемещения. В этом случае одну из двух (две из четырех) проекций не строят, а перечерчивают на кальку, которую затем прикладывают в наиболее удобном месте чертежа. Следующую дополнительную проекцию строят с помощью проекции, изображенной на кальке, и одной из предшествующих.

Способ вращения вокруг главной линии следует рекомендовать для определения натуральной величины плоских фигур и решения метрических задач на плоскости.

Преимущества способа замены плоскостей проекций проявляется в уменьшении количества дополнительных проекций. Он дает наиболее рациональные решения в тех случаях, когда требуется выяснить взаимное расположение геометрических элементов.

Сочетание способа замены плоскостей проекций со способом вращения следует использовать в тех случаях, когда применение каждого из них в отдельности приводит к громоздким и неудобным построениям.

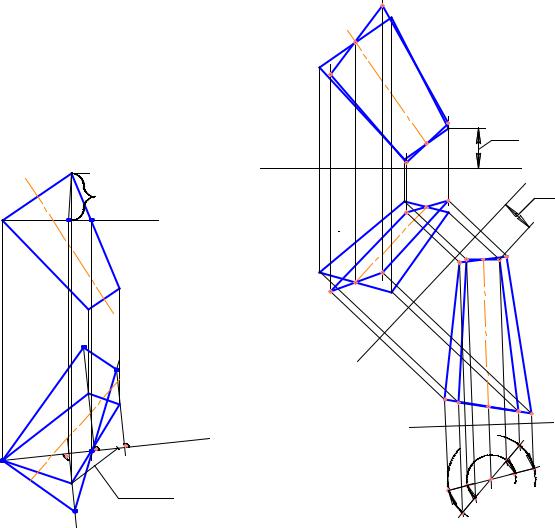
П р и м е р 1. Определить истинную величину лопасти ABCD по ее ортогональному чертежу. Изобразить на чертеже лопасть после поворота на 30º вокруг оси 1 – 2 (рис. 10, 11).

Анализ данных. Лопасть – трапеция, так как AB параллельна DC , которая занимает в

пространстве общее положение.

Анализ решения. Какой метод преобразования чертежа использовать для решения задачи? Для решения первой ее части наиболее удобным будет способ вращения вокруг линии уровня. Решение в данном случае не будет слишком громоздким. Правда, вторую часть задачи этим способом не решить. Здесь следует использовать метод замены плоскостей проекций. Рассмотрим каждую часть задачи отдельно. Решая первую часть (см. рис. 10), мы должны вращением лопасти вокруг линии уровня (например, горизонтали h ) привести ее в частное положение, при котором плоскость трапеции ABCD будет параллельна плоскости проекций (горизонтальной). В этом случае ее проекция на эту плоскость и даст истинную величину. Построить на чертеже проекции линии уровня лежащей в плоскости лопасти не сложно, так как мы знаем, что одна из проекций линии уровня параллельна оси координат, а другую найдем из условия принадлежности. Проекции радиусов вращения вершин трапеции ABCD относительно линии уровня строим, зная теорему о проецировании прямого угла и условия принадлежности. Очевидно, что в положении, при котором лопасть параллельна плоскости проекции, радиусы вращения будут проецироваться на эту плоскость в истинную величину, определяемую способом прямоугольного треугольника.

20

ло перпендикулярно π5 . При этом X2 перпендикулярно 11′′21′′.

4.Строим новую горизонтальную проекцию лопасти, помня о том, что координаты у точек остаются неизменными.

5.Поворачиваем новую горизонтальную проекцию лопасти вокруг оси 1 – 2 на 30º по часо-

вой стрелке в положение A2′ B2′ .

6. Найдем положение точек A2′′B2′′C2′′D2′′, зная, что траектория их перемещения на π4 – прямая, параллельная X 2 .

7. Построим проекции лопасти в системе X π2 после поворота, помня о неизменности ко-

π1

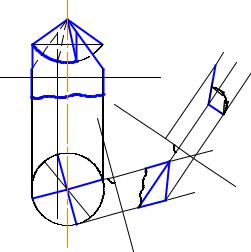
П р и м е р 2. Определить величину угла между гранями ABC и BCD рабочей части фрезы

(рис. 12).

Анализ данных. Положение граней рабочей части фрезы задано однозначно.

Анализ решения. Каким образом на чертеже получить истинную величину искомого угла? Двугранный угол будет проецироваться на плоскость в истинную величину, если плоскость будет перпендикулярна ребру двугранного угла. Ребро – прямая общего положения. Привести ее в проецирующее положение удобно заменой плоскостей проекций.

4. Строим новые горизонтальные проекции ребер BD, AB и BC . Угол α – искомый.

Функционирование космического аппарата (рис. 13) обеспечивается электроэнергией получаемой путем преобразования солнечного излучения. Для преобразования солнечной энергии на панели солнечной батареи располагаются полупроводниковые фотоэлектрические преобразователи (ФЭП). Для наиболее эффективной работы ФЭП необходима ориентация батареи на Солнце таким образом, чтобы солнечные лучи падали на панель батареи под углом близким к 90º.

На рис. 14 приведена конструкция солнечной батареи: 1 – панели; 2 – металлический каркас; 3 – капроновая сетка; 4 – пластины ФЭП.

Формы панелей солнечных батарей могут быть различными. Наиболее часто используются формы (рис. 15).

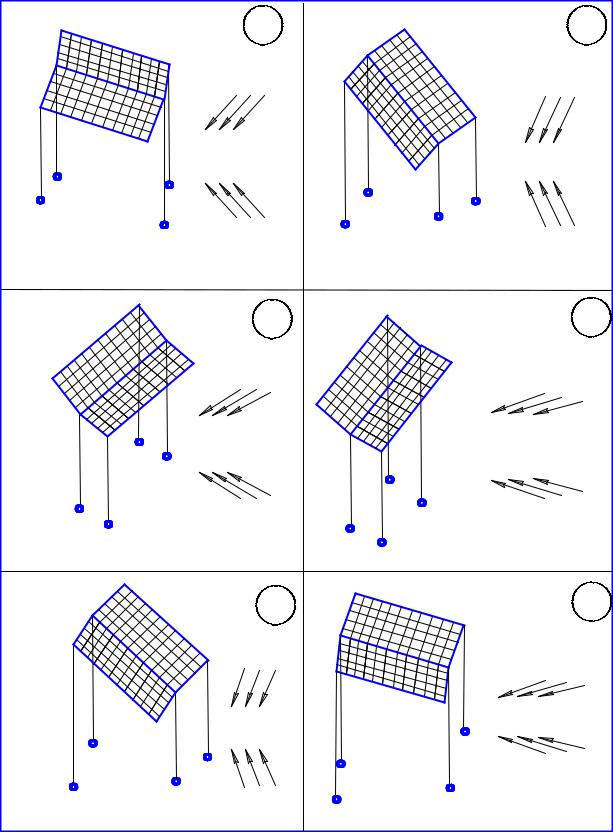
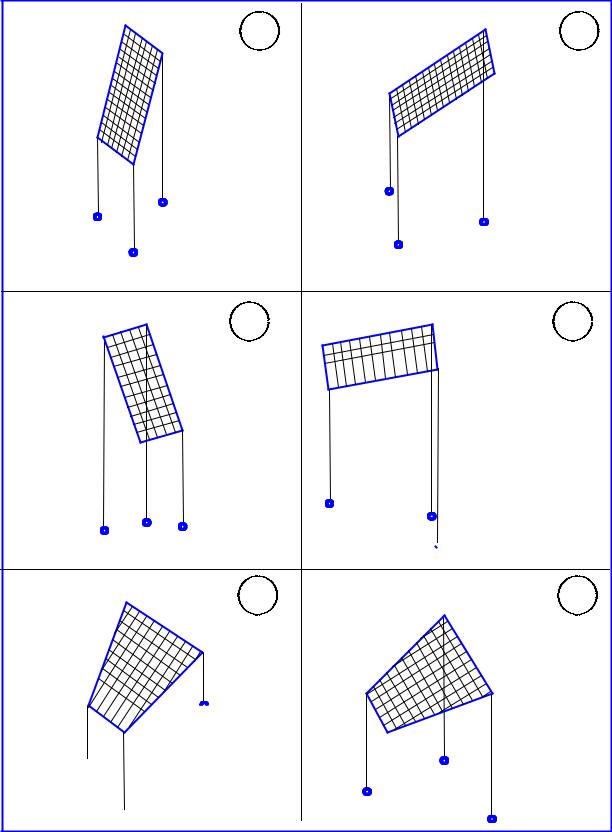
Варианты задания № 3

Варианты 1–12. Дано: ортогональный чертеж панели солнечной батареи. Направление падения солнечных лучей. Определить истинную величину панели и угол между ее плоскостью и направлением солнечных лучей.

Варианты 13–18. Солнечная батарея состоит из двух панелей, направление солнечных лучей l. После поворота вокруг оси 1-2 панель 1-3-4-2 переводится в ту же плоскость, в которой лежит панель 1-2-6-5. Определить необходимый угол поворота и угол между солнечными лучами и полученной плоскостью.

Варианты 19–24. Дано: ортогональный чертеж панели солнечной батареи. Определить двумя способами истинную величину панели и углы наклона панели к плоскостям проекций.

23