4. 5. Деякі застосування подвійних інтегралів

І. Маса області. В попередніх параграфах було показано, що маса неоднорідної області , в кожній площі якої визначена густина розподілу маси, знаходяться за формулою

. (1)

Якщо ж задана на всій площиніі є щільністю розподілу ймовірностей, то за формулою (1) обчислюється ймовірність попадання випадкової точки в область.

ІІ. Обчислення площ плоских областей. Покладемо в (1) , тоді маса чисельно дорівнює площі області . Отже

(2)

формула площі області в прямокутних координатах, а в полярних координатах

. (3)

ІІІ. Обчислення об’єму тіла за допомогою подвійного інтеграла. Тіло, яке обмежене зверху поверхнею , знизу – областюплощини, а збоку – циліндричною поверхнею, твірні якої проходять через границю областіпаралельно осіі перетинають поверхню, називаєтьсявертикальним циліндричним тілом (див. рис. 1)

Об’єм вертикального циліндричного тіла знаходиться за формулою

. (4)

Задача. Обчислити об’єм тіла, обмеженого двома поверхнями і.

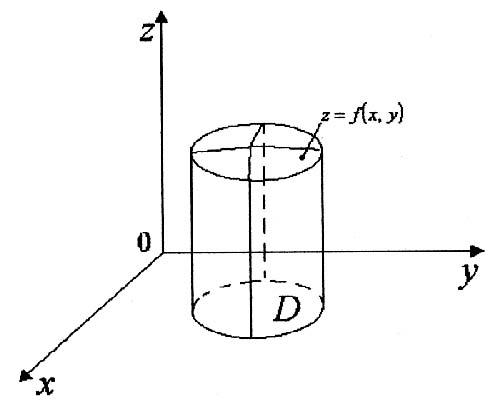
Рис 1.

Розв’язання. Перша з поверхонь – параболоїд обертання навколо осі з вершиною в точці, напрямлений вниз, друга поверхня – конус обертання навколоз вершиною в точці, напрямлений – вверх.

Їх лінії перетину знаходимо із системи:

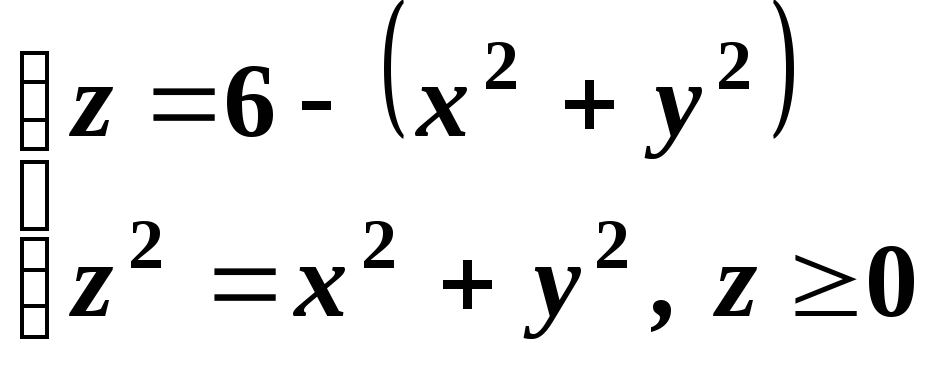
- не підходить. Якщо , то, наприклад, друге рівняння запишеться

.

Отже обидві поверхні перетинаються по колу , яке знаходиться на площині, перпендикулярній(див. рис. 2).

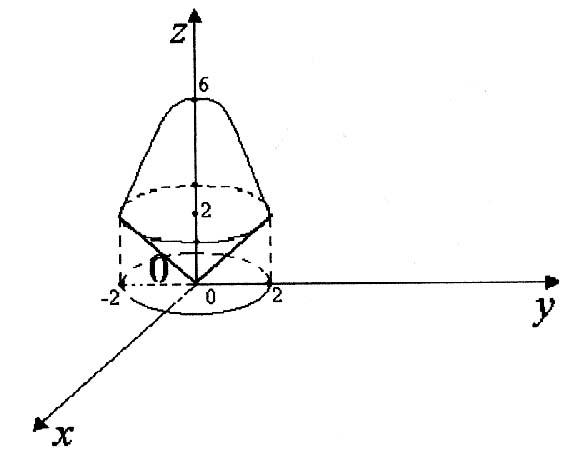
Рис. 2.

Шуканий об’єм тіла дорівнює різниці об’ємів двох циліндричних тілі. Основа обох циліндрів – круг радіусаз центром вна площині. Перше циліндричне тіло обмежене зверху параболоїдом, друге – конусом. Отже,

.

Далі обчислимо в полярних координатах:

.

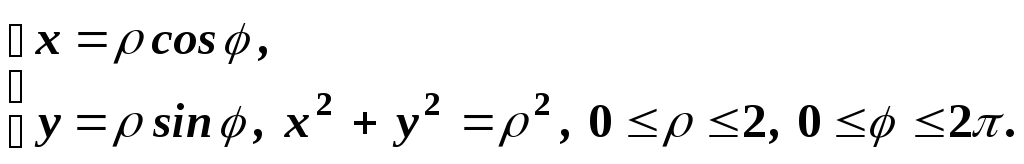
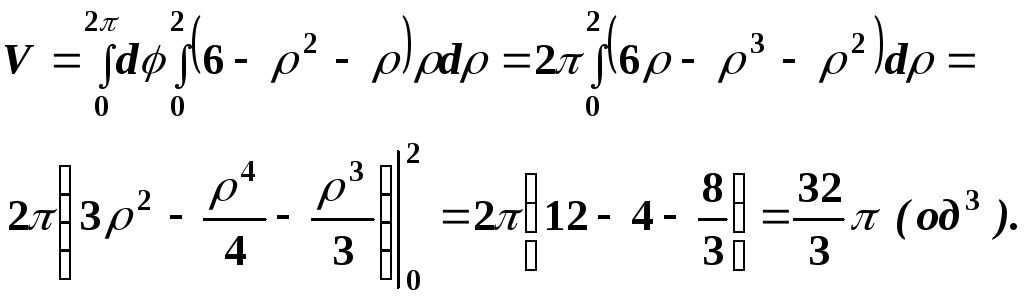
IV. Обчислення статичних моментів, координат центра мас та моментів інерції областей. Статичні моменти ізнаходяться за формулами

, . (5)

Зауважимо, що за подібними формулами з теорії імовірностей знаходяться так звані математичні сподівання двовимірних випадкових величин.

Координати центра маси плоскої області знаходяться за такими формулами

, , (6)

де - маса області.

Моменти інерції івідносно координатних осейіі момент інерціївідносно початку координат знаходяться відповідно за формулами

, , (7)

. (8)

Задачі

Знайти площі плоских областей, обмежених даними лініями

1. .

2. . 3..

4. 5..

6. . 7..

8. . 9..

10. .

11. .

Відповіді: 1. . 2. . 3. . 4. . 5. .

6. . 7. . 8. . 9. . 10. . 11. .

Обчислити об’єми тіл, обмежених даними лініями.

12. .

13. .

14. та координатними площинами.

15. .

16. .

17. .

18. .

19. .

Відповіді: 12. . 13. . 14. . 15. . 16. .

17. . 18. . 19. .

20. Знайти координати центра маси платівки, обмеженої параболою і прямою, якщо густина розподілу маси в кожній точці дорівнює ординаті точки.

21. Знайти центр мас однорідної платівки , обмеженої лініямита.

22. Знайти центр мас однорідної платівки обмеженої параболами .

23. Знайти центр мас плоскої однорідної фігури, обмеженої лініями

.

24. Обчислити момент інерції однорідного квадрата

відносно початку координат.

25.Обчислити момент інерції однорідної фігури, обмеженої

лініями , відносно вісі.

Відповіді: 20. . 21. .