
- •Лабораторна робота № 4 Дослідження гідравлічних опорів по довжині потоку в круглому трубопроводі
- •Загальні положення
- •Послідовність виконання роботи
- •Питання для самоконтролю
- •Лабораторна робота № 5 Визначення коефіцієнтів місцевих гідравлічних опорів
- •Загальні положення
- •Послідовність виконання роботи
- •Питання для самоконтролю
- •Лабораторна робота № 6 Дослідження коефіцієнтів витрати пристроїв, що звужують потік рідини
- •Загальні відомості і теоретичні основи вимірів витрати рідини за допомогою пристроїв, що звужують потік рідини
- •Послідовність виконання роботи
- •Питання для самоконтролю
- •Звіт з лабораторних робіт
- •М. Кривий Ріг
- •2 0 . …
Укладач А.О.Нестеренко
Відповідальний за випуск О.В.Замицький
Рецензент Ю.П.Квятковська
У методичних вказівках наведено мету, послідовність проведення й обробки результатів при виконанні наступних лабораторних робіт: лабораторна робота №4 “Дослідження гідравлічних опорів по довжині потоку в круглому трубопроводі”; лабораторна робота №5 “Визначення коефіцієнтів місцевих гідравлічних опорів”; лабораторна робота №6 “Дослідження коефіцієнтів витрати пристроїв, що звужують потік рідини ”. Наведена послідовність виконання розрахунків, деякі теоретичні положення, таблиці для внесення експериментальних та розрахункових величин, указані літературні та довідкові джерела, послідовність оформлення, а також надано питання для самоконтролю.
Розглянуто Схвалено
на засіданні кафедри на вченій раді
теплоенергетики електротехнічного факультету
Протокол № 2 від 14.11.2010 р. Протокол № 2 від 29.12.2010 р.
Лабораторна робота № 4 Дослідження гідравлічних опорів по довжині потоку в круглому трубопроводі
Мета роботи:
Експериментально визначити величину коефіцієнта гідравлічного опору по довжині потоку при різних швидкостях руху рідини і встановити його залежність від числа Рейнольдса.
Оцінити величину шорсткості трубопроводу експериментальної установки.
Література: [ 4 ],стор. 278-289; [ 5 ],стор. 48-66; [ 6 ],стор. 60-61, додаток 6.8 і 6.9.
Загальні положення
Під час руху реальної рідини на прямолінійних ділянках трубопроводів частина енергії потоку губиться, витрачаючись на долання сил тертя (внутрішнього і зовнішнього). Ці втрати енергії називаються гідравлічними витратами по довжині потоку і визначаються за формулою Дарсі - Вайсбаха:
![]() .
( 4.1)
.
( 4.1)
У цій формулі: λ – коефіцієнт Дарсі або коефіцієнт гідравлічного опору по довжині потоку (величина безрозмірна);
l – довжина трубопроводу, м;
d – внутрішній діаметр трубопроводу, м;
uср – середня швидкість потоку, м/сек.;
g – прискорення вільного падіння, м/сек2.
Витрати тиску по довжині потоку залежать як від режиму руху рідини, так і від шорсткості стінок трубопроводу.
Коефіцієнт гідравлічного опору для ламінарного режиму перебігу рідини визначається теоретично і не залежить від шорсткості стінок λ=ƒ(Re):
![]() ,
( 4.2 )
,
( 4.2 )
де Re – критерій Рейнольдса ( величина безрозмірна).
![]() ,
( 4.3 )
,
( 4.3 )
де ν – коефіцієнт кінематичної густини рідини, м2/сек ;
![]() ,
( 4.4 )
,
( 4.4 )
де Q – витрати рідини, м3/сек;
![]() - площа
«живого» перетину труби, м2.
- площа
«живого» перетину труби, м2.
При турбулентному режимі течії λ залежить від швидкості потоку uср і шорсткості стінок трубопроводу, ∆ мм.
При цьому для гідравлічно гладких труб λ=ƒ(Re) практично не залежить від ∆ і може бути розраховано за формулою Блазіуса:
![]() .
( 4.5 )
.
( 4.5 )
Гідравлічно
гладкими вважаються труби, у яких
відносна шорсткість стінок
![]() =∆/d
не перевищує граничної величини:
=∆/d
не перевищує граничної величини:
![]() гр
гр
![]() .
( 4.6 )
.
( 4.6 )
Для труб з помірною шорсткістю λ=ƒ(Re,∆) може бути розраховано за формулою Альтшуля:
![]() ,
( 4.7 )
,
( 4.7 )
де ∆ - абсолютна шорсткість стінок трубопроводу, мм.
При розвиненій шорсткості на коефіцієнт гідравлічного опору основний вплив чинить шорсткість стінок ( λ=ƒ(∆) ), для якого Нікурадзе отримав емпіричну залежність :
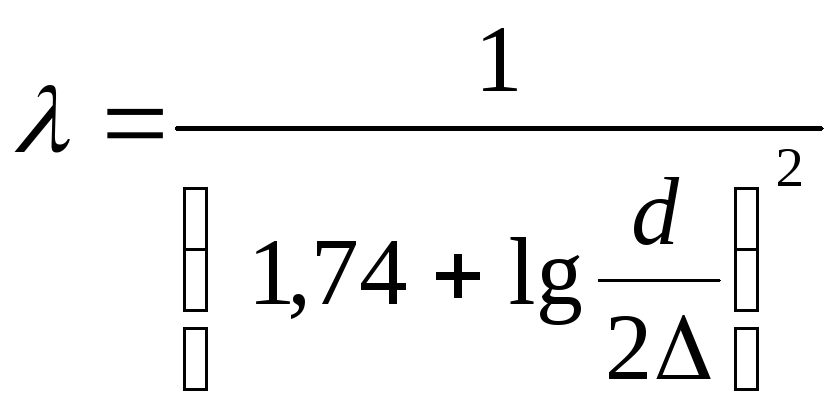 .
( 4.8 )
.
( 4.8 )
Необхідно відзначити, що формули ( 4.7 ) і ( 4.8 ) отримано для штучної, так званої “пісочної“ шорсткості. Експериментально встановлено, що в технічних трубах має місце “хвиляста“ шорсткість, яка при однакових величинах “пісочною“ шорсткістю приводить до збільшених значень коефі-
цієнта λ, залежно від Re і величини шорсткості.
На рис.4.1 наведені експериментальні дані для технічних труб, отри –
мані у
ВТІ Г.А.Муріним, який виділяє три
діапазони : І-й діапазон ламінарної
течії, де коефіцієнт λ=ƒ(Re)
і крива 1 співпадають з даними, розра
хованими за формулою ( 4.2 ) ; І І – й
діапазон помірної шорсткості. У цьому
діапазоні коефіцієнт λ=ƒ(Re,
![]() );
його значення розташовані між кривою
2, яка відповідає гідравлічно гладким
трубам, і практично співпадають з
);
його значення розташовані між кривою
2, яка відповідає гідравлічно гладким
трубам, і практично співпадають з
даними, отриманими під час розрахунку за формулою( 4.5 ) коли Re ≤ 1∙105
і –
умовною штриховою кривою 3 ; ІІІ – й
діапазон розвиненої шорсткості, який
розташований над кривою 3, у якому
коефіцієнт λ=ƒ(![]() ).
).
Для
практичних розрахунків діапазон помірної
шорсткості
![]() п
допускається
обмежити зверху пунктирною кривою 4,
яка розташована над кривою 2 – гідравлично
гладких труб, згідно з умовою :
п
допускається
обмежити зверху пунктирною кривою 4,
яка розташована над кривою 2 – гідравлично
гладких труб, згідно з умовою :
![]() пр
≤
пр
≤
![]() п
≤8
∙
п
≤8
∙![]() пр
,
( 4.9 )
пр
,
( 4.9 )
тоді формули ( 4.7 ) і ( 4.8 ) з поправочними коефіцієнтами можуть бути використані для розрахунків коефіцієнта λ технічних труб у діапазоні чисел Рейнольдса 4000 < Re ≤ 1∙107 .
Для діапазону помірної шорсткості :
![]()
![]() , (
4.10 )
, (
4.10 )
де kп = 1,21 – поправочний коефіцієнт діапазону помірної шорсткості.
Для діапазону розвиненої шорсткості :
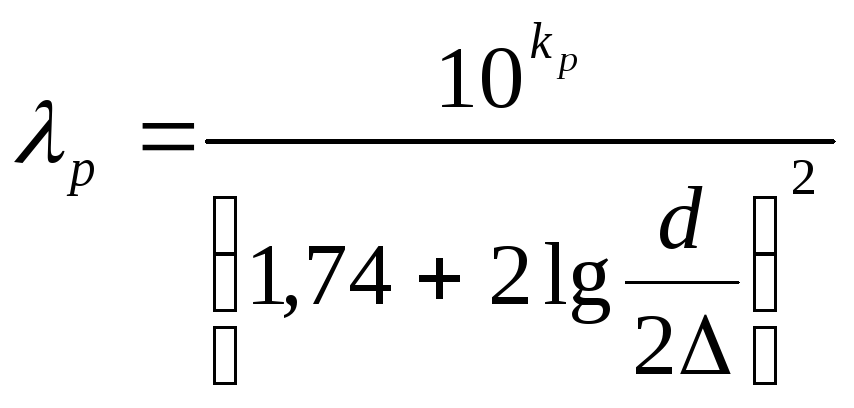 , (
4.11 )
, (
4.11 )
де kр – поправочний коефіцієнт діапазону розвиненої шорсткості (табл.4.1.)
Таблиця 4.1
|
|
1∙10-5 |
1 ∙ 10-4 |
1 ∙ 10-3 |
1 ∙ 10-2 |
5 ∙ 10-2 |
6 ∙ 10-2 |
7 ∙ 10-2 |
8 ∙10-2 |
|
kр |
1,25 |
0,85 |
0,5 |
0,12 |
0,01 |
0 |
0,04 |
0,006 |
|
λр(ф.4.11) |
0,009 |
0,014 |
0,022 |
0,037 |
0,074 |
0,08 |
0,09 |
0,1 |
Величина числа Рейнольдса, при якому відбувається зміна режимів руху рідини, називається критичним числом Рейнольдса – Reкр.
Під час руху рідини в круглому трубопроводі приймають Reкр =2300.
Таким чином, якщо отримана при розрахунках величина числа Рейнольдса менше критичного числа, тобто Re < Reкр – режим руху рідини ламінарний, а якщо Re > Reкр - режим руху рідини турбулентний.
