2_1-2_136

. (6)

Звідки отримаємо зміну температури

. (7)

Підставляємо в формулу (7) данні умови задачі, виражені в системі СІ, і отримаємо відповідь:

=

101. Яку роботу треба здійснити, щоб розділити сферичну краплю ртуті радіусом R =3 мм на дві однакові краплі?

2.103.

Розв’язок.

Д

Дано

R = 3 мм = 0,5 Дж/м2

= ?

одаткова енергія, яку мають молекули в поверхневому шарі рідини, отримала назву поверхневої і визначається таким чином:

, (1)

де  - поверхневий натяг; S – площа поверхневого шару, м².

Оскільки каплю ділимо на дві однакові краплі, то зміна площі поверхневого шару дорівнюватиме

, (2)

де - діаметр великої кулі, який знаходимо з рівності об’ємів великої кулі суми маленьких:

. (3)

Тоді зміну поверхні отримаємо підстановкою радіуса малої краплі з виразу (3) у вираз (2):

, (4)

Підставляємо вираз з (4) у формулу енергії (1) і отримаємо вираз для розрахунку работи:

= (5)

Підставляємо в формулу (5) данні умови задачі, виражені в системі СІ, і отримаємо відповідь:

=

101. Яку роботу проти сил поверхневого натягу треба здійснити, щоб збільшити вдвічі об'єм мильної бульбашки радіусом R = 1 см? Поверхневий натяг мильного розчину  = 0,043 Н/м.

2.104.

Дано

R = 1 см = 0,043 Н/м

= ?

Розв’язок.

Додаткова енергія, яку мають молекули в поверхневому шарі рідини, отримала назву поверхневої і визначається таким чином:

, (1)

де  - поверхневий натяг; S – площа поверхневого шару, м².

Оскільки необхідно збільшити вдвічі об'єм мильної бульбашки, то підрахуємо на скільки збільштеся площа її вільної поверхні, враховуючи що бульбашка має зовнішню і внутрішню поверхню:

, (2)

де - радіус великої бульбашки, який знаходимо з умови задачі:

. (3)

Тоді зміну поверхні отримаємо підстановкою радіуса великої бульбашки з виразу (3) у вираз (2):

, (4)

Підставляємо вираз з (4) у формулу енергії (1) і отримаємо вираз для розрахунку роботу:

(5)

Підставляємо в формулу (5) данні умови задачі, виражені в системі СІ, і отримаємо відповідь:

=

101. Яку роботу проти сил поверхневого натягу треба здійснити, щоб видути мильну бульбашку діаметром d = 4 см? Поверхневий натяг мильного розчину  = 0,043 Н/м.

2.105.

Дано

d = 4 см = 0,043 Н/м

= ?

Розв’язок.

Додаткова енергія, яку мають молекули в поверхневому шарі рідини, отримала назву поверхневої і визначається таким чином:

, (1)

де  - поверхневий натяг; S – площа поверхневого шару, м².

Оскільки необхідно видути мильну бульбашку, то підрахуємо на скільки збільштеся площа її вільної поверхні, враховуючи що бульбашка має зовнішню і внутрішню поверхню:

, (2)

Підставляємо вираз з (2) у формулу енергії (1) і отримаємо вираз для розрахунку роботи:

(5)

Підставляємо в формулу (5) данні умови задачі, виражені в системі СІ, і отримаємо відповідь:

=

101. Знайти тиск повітря у повітряній бульбашці діаметром d = 0,01 мм, що знаходиться на глибині h = 20 см під поверхнею води. Атмосферний тиск _о = 101,7 кПа.

2.106.

Дано

= 0,01 мм = 0,073 Н/м h = 20 см = 101,7 кПа

= ?

Розв’язок.

Надлишковий тиск, зумовлений кривизною поверхні рідини (формула Лапласа), для сферичної поверхні:

. (1)

Тоді повний тиск дорівнюватиме

. (2)

де - риск водяного стовпа.

Після підстановки у формулу (2) даних умови задачі, отримаємо відповідь

=

101. Тиск повітря всередині мильної бульбашки на  = 133,3 Па більше атмосферного. Знайти її діаметр. Поверхневий натяг мильного розчину  = 0,043 Н/м.

2.107.

Дано

= 0,043 Н/м  = 133,3 Па

= ?

Розв’язок.

Надлишковий тиск, зумовлений кривизною поверхні рідини (формула Лапласа), для сферичної поверхні:

. (1)

Згідно з умовою надлишковий тиск дорівнює . Тоді діаметр бульбашки дорівнюватиме

. (2)

Після підстановки у формулу (2) даних умови задачі, отримаємо відповідь

=

101. Маса m = 10 г реального гелію займає об'єм V = 100 см³ при тиску = 100 МПа. Знайти температуру газу.

2.108.

Дано

m = 10 г = 4∙10-3 кг/моль = 100 см3 = 100 МПа

= ?

Розв’язок.

Рівняння Ван-дер-Ваальса для одного молю газу має вигляд

, (.1)

а для довільної маси газу

, (2)

де = і — сталі Ван-дер-Ваальса. В цьому рівнянні —тиск, зумовлений силами взаємодії молекул, — об'єм, зв'язаний з власним об'ємом молекул.

Зв'язок критичних параметрів — молярного об'єму, тиску і температури газу — із сталими і Ван-дер-Ваальса

. (3)

Сталу знайдемо з другого та квадрату третього рівнянь з (3):

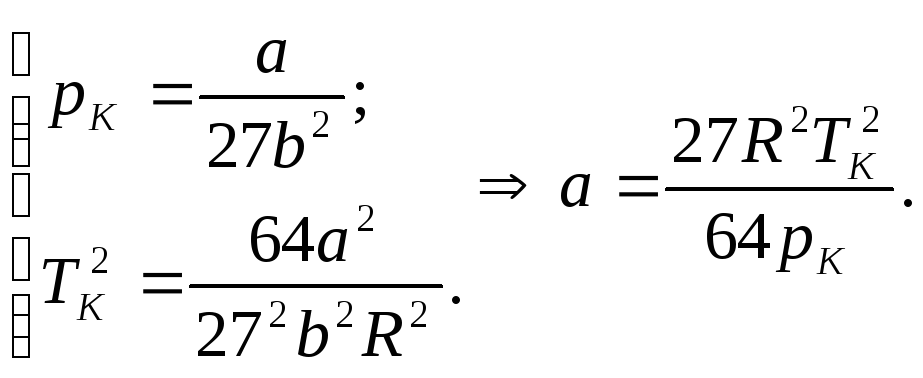(4)

А сталу визначаємо поділивши одне на одне друге та третє рівняння з (3)

, (5)

де = 5,2 К, = 0,23 МПа – критичні параметри для гелію.

Отримані сталі Ван-дер-Ваальса з формул (4) і (5) підставляємо у формулу (2) та розв’язуємо її відносно температури:

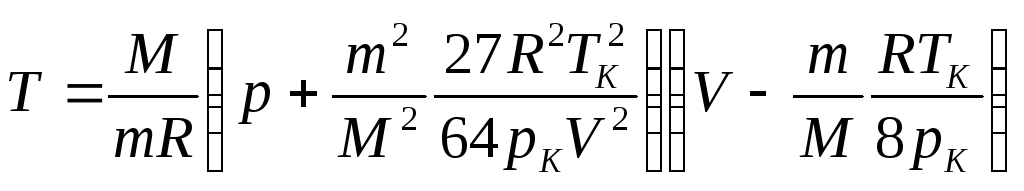, (6)

Підставляємо у вираз (6) даних умови і отримаємо відповідь:

=

101. Один кмоль вуглекислого газу знаходиться при температурі Т = 100°С. Знайти тиск газу, вважаючи його реальним. Задачу розв’язати для об'ємів V₁ = l м³ і V₂ = 0,05 м³.

2.109.

Дано

= 1 кмоль = 44∙10-3 кг/моль Т = 100°С V1 = l м3 V2 = 0,05 м3 = 100 МПа

= ? = ?

Розв’язок.

Рівняння Ван-дер-Ваальса для одного молю газу має вигляд

, (.1)

а для довільної маси газу

, (2)

де = і — сталі Ван-дер-Ваальса. В цьому рівнянні —тиск, зумовлений силами взаємодії молекул, — об'єм, зв'язаний з власним об'ємом молекул.

Зв'язок критичних параметрів — молярного об'єму, тиску і температури газу — із сталими і Ван-дер-Ваальса

. (3)

Сталу знайдемо з другого та квадрату третього рівнянь з (3):

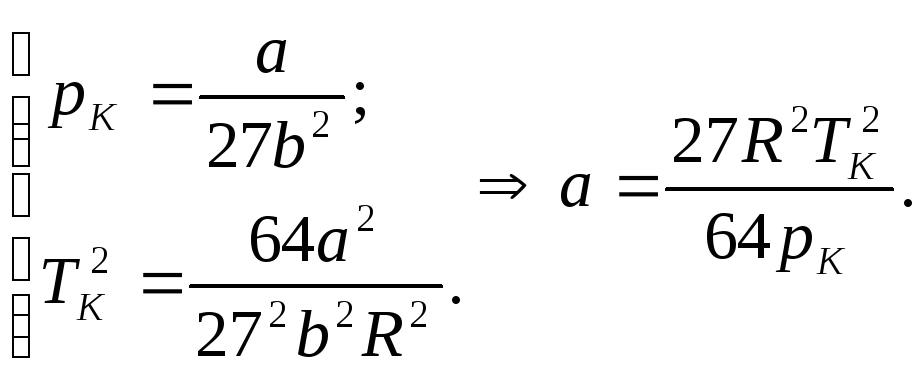(4)

А сталу визначаємо поділивши одне на одне друге та третє рівняння з (3)

, (5)

де = 304 К, = 7,4 МПа – критичні параметри для вуглекислого газу.

Отримані сталі Ван-дер-Ваальса з формул (4) і (5) підставляємо у формулу (2) та розв’язуємо її відносно тиску:

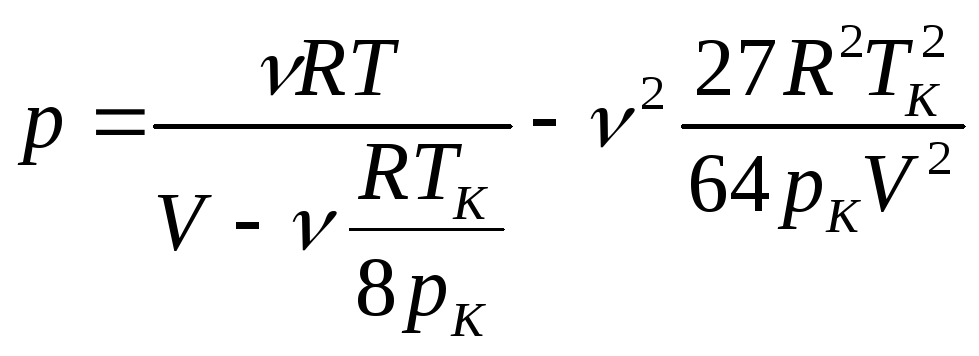, (6)

Підставляємо у вираз (6) даних умови і отримаємо відповіди:

= =

2.110. Знайти зміну ентропії при переході = 8 г кисню від об'єму = 10 л при температурі t₁ = 80°С до об'єму = 40 л при температурі t₂ = 300°С.

2.110.

Дано

= 8 г = 32∙10-3 кг/м3 V1 = 10 л t1 = 80°С V2 = 40 л t2 = 300°С

= ?

Розв’язок.

Для любого оборотного кругового процесу, сума зведених кількостей теплоти дорівнює нулю. Тобто:

. (1)

З рівності нулю цього інтеграла слідує, що підінтегральний вираз дорівнює повному диференціалу деякої функції, яка визначається тільки станом термодинамічної системи і не залежить від способу переходу до цього стану. Тобто:

. (2)

Приріст ентропії при переході термодинамічної системи із стану 1 у стан 2 дорівнює

. (3)

Таким чином, зміна ентропії при переході ідеального газу з одного стану у другий, не залежить від виду термодинамічного процесу і, з урахуванням першого принципу термодинаміки:

, (4)

де - елементарна кількість теплоти, що підводиться до термодинамічної системи; - зміна внутрішньої енергії системи; - робота, виконувана системою проти зовнішніх сил при нескінченно малій зміні об’єму, тоді, після інтегрування, маємо

. (5)

Молярну теплоємність газу для випадку його участі в ізохорному процесі

, (6)

= 5 - кількість ступенів вільності молекул газу.

З урахуванням теплоємності з виразу (6), вираз (5) прийме вигляд:

. (7)

Підставляємо в формулу (7) данні умови задачі, виражені в системі СІ, і отримаємо відповідь:

=

111. Знайти зміну ентропії при переході = 6 г водню від об'єму V₁ = 10 л під тиском =150 кПа до об'єму V₂ = 60 л під тиском = 100 кПа.

2.111.

Дано

= 6 г = 2∙10-3 кг/м3 V1 = 10 л =150 кПа V2 = 60 л = 100 кПа

= ?

Розв’язок.

Для любого оборотного кругового процесу, сума зведених кількостей теплоти дорівнює нулю. Тобто:

. (1)

З рівності нулю цього інтеграла слідує, що підінтегральний вираз дорівнює повному диференціалу деякої функції, яка визначається тільки станом термодинамічної системи і не залежить від способу переходу до цього стану. Тобто:

. (2)

Приріст ентропії при переході термодинамічної системи із стану 1 у стан 2 дорівнює

. (3)

Таким чином, зміна ентропії при переході ідеального газу з одного стану у другий, не залежить від виду термодинамічного процесу і, з урахуванням першого принципу термодинаміки:

, (4)

де - елементарна кількість теплоти, що підводиться до термодинамічної системи; - зміна внутрішньої енергії системи; - робота, виконувана системою проти зовнішніх сил при нескінченно малій зміні об’єму, тоді, після інтегрування, маємо

. (5)

Молярну теплоємність газу для випадку його участі в ізохорному процесі

, (6)

= 5 - кількість ступенів вільності молекул газу.

З системи рівнянь Менделєєва — Клапейрона для двох станів газу:

(7)

Отримаємо відношення температур:

. (8)

З урахуванням теплоємності з виразу (6) відношення температур з виразу (8), вираз (5) прийме вигляд:

. (9)

Підставляємо в формулу (9) данні умови задачі, виражені в системі СІ, і отримаємо відповідь:

=

111. Маса m = 6,6 г водню ізобарно розширяється від об'єму V₁ до об'єму V₂ = 2V₁. Знайти зміну ентропії при цьому розширенні.

2.112.

Дано

= 6,6 г = 2∙10-3 кг/м3 = V2 = 2∙V1

= ?

Розв’язок.

Для любого оборотного кругового процесу, сума зведених кількостей теплоти дорівнює нулю. Тобто:

. (1)

З рівності нулю цього інтеграла слідує, що підінтегральний вираз дорівнює повному диференціалу деякої функції, яка визначається тільки станом термодинамічної системи і не залежить від способу переходу до цього стану. Тобто:

. (2)

Приріст ентропії при переході термодинамічної системи із стану 1 у стан 2 дорівнює

. (3)

Таким чином, зміна ентропії при переході ідеального газу з одного стану у другий, не залежить від виду термодинамічного процесу і, з урахуванням першого принципу термодинаміки:

, (4)

де - елементарна кількість теплоти, що підводиться до термодинамічної системи; - зміна внутрішньої енергії системи; - робота, виконувана системою проти зовнішніх сил при нескінченно малій зміні об’єму, тоді, після інтегрування, маємо

. (5)

Молярну теплоємність газу для випадку його участі в ізохорному процесі

, (6)

= 5 - кількість ступенів вільності молекул газу.

З системи рівнянь Менделєєва — Клапейрона для двох станів газу:

(7)

Отримаємо відношення температур:

. (8)

З урахуванням теплоємності з виразу (6) відношення температур з виразу (8), вираз (5) прийме вигляд:

. (9)

Підставляємо в формулу (9) данні умови задачі, виражені в системі СІ, і отримаємо відповідь:

=

111. На скільки тиск повітря всередині мильної бульбашки діаметром d = 5 мм більше нормального атмосферного тиску ?

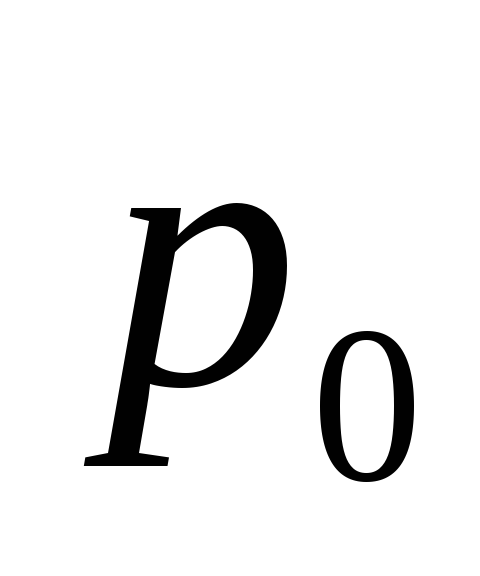2.113.

Дано

= 5 мм = 0,043 Н/м = 105 Па

= ?

Розв’язок.

Надлишковий тиск, зумовлений кривизною поверхні рідини (формула Лапласа), для сферичної поверхні:

. (1)

Згідно з умовою надлишковий тиск дорівнює . Тоді маємо

. (2)

Після підстановки у формулу (2) даних умови задачі, отримаємо відповідь

=

111. Знайти зміну ентропії при ізотермічному розширенні = 6 г водню від тиску = 100 кПа до тиску = 50 кПа.

2.114.

Дано

= 6 г = 2∙10-3 кг/м3 = = 100 кПа = 50 кПа

= ?

Розв’язок.

Для любого оборотного кругового процесу, сума зведених кількостей теплоти дорівнює нулю. Тобто:

. (1)

З рівності нулю цього інтеграла слідує, що підінтегральний вираз дорівнює повному диференціалу деякої функції, яка визначається тільки станом термодинамічної системи і не залежить від способу переходу до цього стану. Тобто:

. (2)

Приріст ентропії при переході термодинамічної системи із стану 1 у стан 2 дорівнює

. (3)