2_1-2_136

. (5)

Відношення до дорівнює

. (6)

Розпишемо рівняння (2)

. (7)

Звідки отримаємо

. (8)

Після підстановки виразу для з (6) у формулу (8) та даних умови задачі, отримаємо відповідь

=

59. Об'єм V₁ = 7,5 л кисню адіабатичним чином стискується до об'єму V₂ = 1 л, причому у кінці стиснення встановився тиск = 1,6 МПа. Під яким тиском знаходився газ до стиснення?

2.80.

Дано

V1 = 7,5 л V2 = 1 л = 1,6 МПа V2 = 2V1 = 5

= ?

Розв’язок.

Рівняння адіабатного процесу (рівняння Пуассона) мають вигляд

, (1)

або , (2)

або , (3)

де — показник адіабати. Молярну теплоємність газу для випадку його участі в ізохорному процесі визначають за формулою:

, (4)

- кількість ступенів вільності молекул газу.

Молярна теплоємність газу при ізобарному процесі (рівняння Майєра) визначається формулою:

. (5)

Відношення до дорівнює

. (6)

Розпишемо рівняння (1)

. (7)

Звідки отримаємо

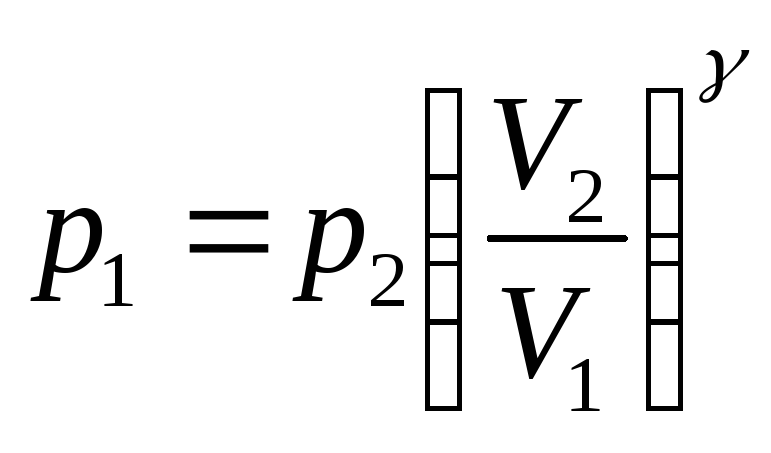. (8)

Після підстановки виразу для з (6) у формулу (8) та даних умови задачі, отримаємо відповідь

=

59. За умови адіабатичного стиснення повітря в циліндрах двигуна внутрішнього згорання тиск змінюється від 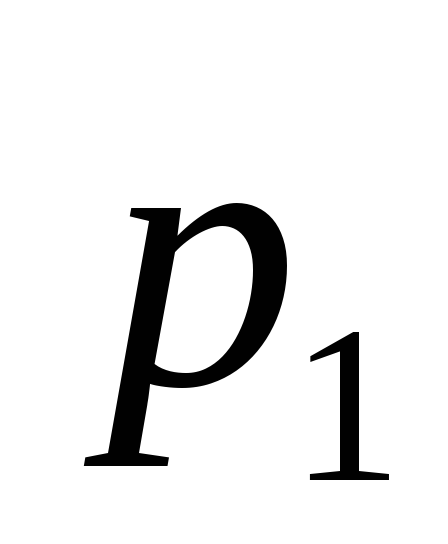= 0,l МПа до = 3,5 МПа. Початкова температура повітря t₀ = 40°С. Знайти температуру t повітря у кінці стиснення.

2.81.

Дано

= 0,l МПа = 3,5 МПа = t0 = 40°С = 5

= ?

Розв’язок.

Рівняння адіабатного процесу (рівняння Пуассона) мають вигляд

, (1)

або , (2)

або , (3)

де — показник адіабати. Молярну теплоємність газу для випадку його участі в ізохорному процесі визначають за формулою:

, (4)

- кількість ступенів вільності молекул газу.

Молярна теплоємність газу при ізобарному процесі (рівняння Майєра) визначається формулою:

. (5)

Відношення до дорівнює

. (6)

Розпишемо рівняння (3)

. (7)

Звідки отримаємо

. (8)

Після підстановки виразу для з (6) у формулу (8) та даних умови задачі, отримаємо відповідь

=

59. Газ розширяється за законом адіабати, причому об'єм його збільшується вдвічі, а термодинамічна температура падає у 1,32 рази. Яке число ступенів свободи мають молекули цього газу?

Дано

= 2, = 1,32

= ?

2.82.

Розв’язок.

Рівняння адіабатного процесу (рівняння Пуассона) мають вигляд

, (1)

або , (2)

або , (3)

де — показник адіабати. Молярну теплоємність газу для випадку його участі в ізохорному процесі визначають за формулою:

, (4)

- кількість ступенів вільності молекул газу.

Молярна теплоємність газу при ізобарному процесі (рівняння Майєра) визначається формулою:

. (5)

Відношення до дорівнює

. (6)

Розпишемо рівняння (2)

. (7)

Звідки отримаємо

. (8)

Логарифмуємо вираз (8)

. (9)

З виразу (9) отримаємо

. (10)

Враховуючі вираз (6) отримаємо формулу для розрахунку:

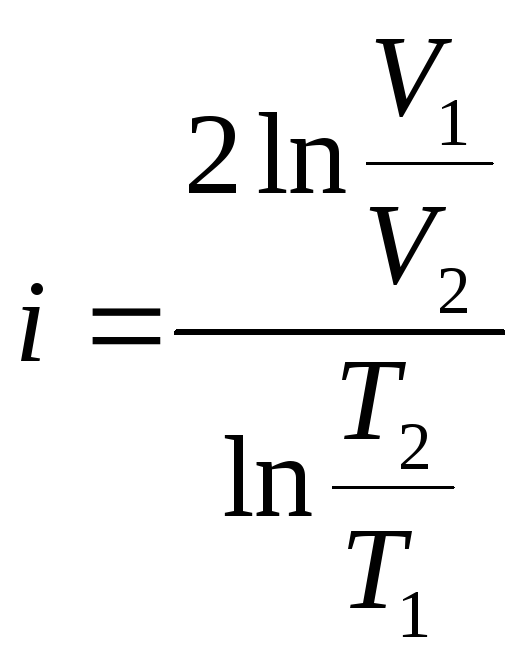. (11)

Після підстановки у формулу (11) даних умови задачі, отримаємо відповідь

=

59. Двоатомний газ, що знаходиться під тиском ₀ = 2 МПа, з температурою t₀ = 27°С, стискується за законом адіабати від об'єму V₀ до V₁ = 0,5V₀. Знайти температуру t₁ і тиск газу після стиснення.

2.83.

Дано

0 = 2 МПа t0 = 27°С V1 = 0,5V0 = 5

= ? = ?

Розв’язок.

Рівняння адіабатного процесу (рівняння Пуассона) мають вигляд

, (1)

або , (2)

або , (3)

де — показник адіабати. Молярну теплоємність газу для випадку його участі в ізохорному процесі визначають за формулою:

, (4)

- кількість ступенів вільності молекул газу.

Молярна теплоємність газу при ізобарному процесі (рівняння Майєра) визначається формулою:

. (5)

Відношення до дорівнює

. (6)

Розпишемо рівняння (2)

. (7)

Звідки отримаємо

. (8)

Розпишемо рівняння (1)

. (9)

Звідки отримаємо

. (10)

Після підстановки виразу для з (6) у формули (8) і (10) та даних умови задачі, отримаємо відповідь

= =

59. У посудині під поршнем знаходиться гримучий газ, що займає при нормальних умовах об'єм V = 0,1 л. При швидкому стисненні газ запалюється. Знайти температуру Т запалення гримучого газу, якщо відомо, що робота стиснення А = 46,35 Дж.

2.84.

Дано

= 105 Па = 273 К V = 0,1 л А = 46,35 Дж = 5

= ?

Розв’язок.

Процес стиснення газу можна вважати адіабатним, для якого = . Тоді

. (1)

Звідки отримаємо температуру Т = запалення гримучого газу

. (2)

Відношення визначаємо з рівняння Менделєєва — Клапейрона:

. (3)

Вираз (3) підставляємо у формулу (2) і отримаємо розрахункову формулу:

= (4)

Після підстановки у формулу (4) даних умови задачі, отримаємо відповідь

=

59. У посудині під поршнем знаходиться газ при нормальних умовах. Відстань між дном посудини і дном поршня 25 см. Коли на поршень поклали вантаж масою 20 кг, поршень опустився на 13,4 см. Вважаючи стиснення адіабатичним, знайти для даного газу відношення с_p/с_v. Площа поперечного перетину поршня s = 10 см².

2.85.

Дано

= 105 Па = 273 К = 25 см = 20 кг = 13,4 см s = 10 см2

= ?

Розв’язок.

Рівняння адіабатного процесу (рівняння Пуассона) мають вигляд

, (1)

або , (2)

або , (3)

де — показник адіабати. Молярну теплоємність газу для випадку його участі в ізохорному процесі визначають за формулою:

, (4)

- кількість ступенів вільності молекул газу.

Молярна теплоємність газу при ізобарному процесі (рівняння Майєра) визначається формулою:

. (5)

Відношення до дорівнює

. (6)

Розпишемо рівняння (1)

. (7)

Звідки отримаємо

, (8)

де тиск газу зросте до величини

, (9)

а об’єм зменшиться до величини

. (10)

Вирази (9) і (10) у формулу (8) і отримаємо формулу для розрахунку:

, (11)

Після підстановки у формули (11) даних умови задачі, отримаємо відповідь

=

59. Двоатомний газ займає об'єм = 0,5 л при тиску = 50 кПа. Газ стискується адіабатичним способом до деякого об'єму V₂ та тиску 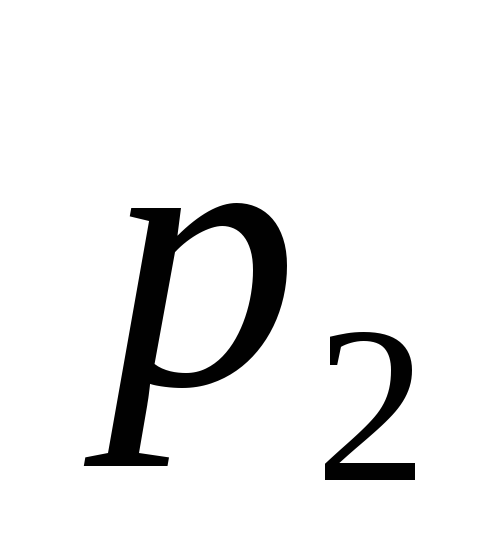. Потім він охолоджується при V₂ = const до початкової температури, причому його тиск стає рівним = 100 кПа. Знайти об'єм V₂ і тиск .

Рис. 2.86

2.86.

Дано

= 5 = 0,5 л = 50 кПа = 100 кПа

= ? = ?

Розв’язок.

Зробимо малюнок.

Рівняння адіабатного процесу (рівняння Пуассона) мають вигляд

, (1)

або , (2)

або , (3)

де — показник адіабати. Рівняння (1) – (3) перетворюються одне в друге завдяки використанню рівнянню Менделєєва – Клапейрона.

Молярну теплоємність газу для випадку його участі в ізохорному процесі визначають за формулою:

, (4)

- кількість ступенів вільності молекул газу.

Відношення до дорівнює

. (6)

Розпишемо рівняння (1) для першого процесу

. (7)

З рівняння (7) отримаємо

. (8)

З рівняння Менделєєва – Клапейрона для першого і останнього стану газу отримаємо:

(9)

отримаємо

. (10)

А з ізохорного процесу отримаємо

. (11)

З рівнянь (10) і (11) отримуємо

. (12)

А з рівнянь (8) та (12) маємо

. (13)

Після перетворень отримаємо вираз для визначення тиску :

. (14)

А з рівняння (8) та (14) отримаємо вираз для розрахунку об’єму :

. (15)

Після підстановки у формули (15) і (14) даних умови задачі, отримаємо відповідь

= =

59. Газ розширяється за законом адіабати так, що його тиск падає від = 200 кПа до = 100 кПа. Потім він нагрівається при постійному об'ємі до початкової температури, причому його тиск стає рівним 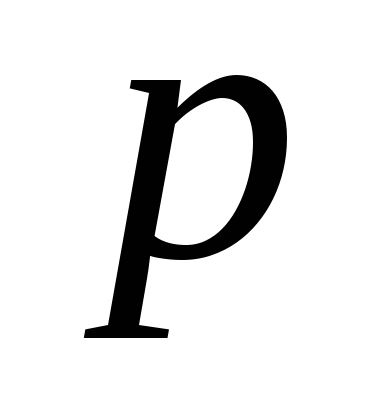= 122 кПа. Знайти відношення с_p/с_v. для цього газу.

Рис. 2.86

2.87.

Дано

= 200 кПа = 100 кПа = 122 кПа

= ?

Розв’язок.

Зробимо малюнок.

Перший процес адіабатичний. Рівняння адіабатного процесу (рівняння Пуассона) мають вигляд

, (1)

або , (2)

або , (3)

де — показник адіабати. Рівняння (1) – (3) перетворюються одне в друге завдяки використанню рівнянню Менделєєва – Клапейрона.

Молярну теплоємність газу для випадку його участі в ізохорному процесі визначають за формулою:

, (4)

- кількість ступенів вільності молекул газу.

Відношення до дорівнює

. (6)

Розпишемо рівняння (1) для першого процесу

. (7)

З рівняння (7) отримаємо

. (8)

З другого, ізохорного процесу:

, (9)

отримаємо

. (10)

Підставляємо температуру з виразу (10) у вираз (8)

. (11)

Логарифмуємо вираз (11)

. (12)

З виразу (12) отримаємо відповідь:

. (13)

Після підстановки у формулу (13) даних умови задачі, отримаємо відповідь

=

59. Яку енергію треба затратити, щоб видути мильний пузир діаметром = 12 см? Яким буде додатковий тиск всередині цього пузиря?

2.88.

Дано

= 12 см = 0,043 Дж/м2

= ? = ?

Розв’язок.

Додаткова енергія, яку мають молекули в поверхневому шарі рідини, отримала назву поверхневої і визначається таким чином:

, (1)

де  - поверхневий натяг; S – площа поверхневого шару, м².

Оскільки мильний пузир має зовнішній і внутрішній шар молекул, площа поверхні яких майже рівні, то енергія дорівнюватиме

. (2)

Надлишковий тиск, зумовлений кривизною поверхні рідини (формула Лапласа), для сферичної поверхні:

. (3)

Після підстановки у формули (2) і (3) даних умови задачі, отримаємо відповідь

= =

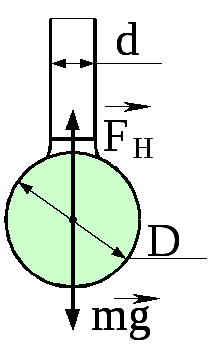
59. На нижньому кінці трубки діаметром d = 0,2 см, висить сферична крапля води. Знайти діаметр цієї краплі.

2.89.

Рис. 2.89

Дано

d = 0,2 см

= ?

Розв’язок.

Зробимо малюнок.

Крапля відірветься від трубки коли її вага перевищить силу поверхневого натягу, що діє в найменшому по діаметру контуру в місті з’єднання краплі з трубкою.

. (1)

Будемо вважати, що цей діаметр дорівнює діаметру трубки . Тоді з формули коефіцієнта поверхневого натягу можна визначити силу натягу:

, (2)

де — сила поверхневого натягу; — довжина ділянки контуру, що обмежує вільну поверхню.

З рівнянь (1) і (2) отримуємо рівняння

. (3)

де - густина води, кг/м³.

Розв’язуємо рівняння (3) відносно діаметра краплі

= (4)

Підставляємо в формулу (4) данні умови задачі, виражені в системі СІ, і отримаємо відповідь:

=

59. Гас витікає з вертикальної трубки діаметром = 1,8 мм. Скільки крапель вийде з = 1 граму гасу, якщо коефіцієнт поверхневого натягу гасу = 24 10^-3 Н/м, g = 10 м/с² ?