Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Криворожский национальный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2_1-2_136

.doc

Скачиваний:

168

Добавлен:

07.03.2016

Размер:

3.7 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 113 4 5 6 7 8 9 10 11 > Следующая >>>

, (4)

де  - кількість молів речовини.

Кількість молів речовини визначимо з рівняння стану ідеального газу (рівняння Менделєєва — Клапейрона):

, (5)

де = 8,31 Дж/(моль•К) — універсальна газова стала.

Кількість молів речовини з рівняння (5) підставляємо у вираз (4)

, (6)

Молярні теплоємкості газу при ізобарному і ізохорному процесі пов’язані рівнянням Майора, з якого отримаємо:

, (7)

Теплоємності з виразів (6) та (7) підставляємо у формулу (1) і отримаємо вираз для розрахунку:

= (8)

Підставляємо дані умови в рівняння (8) та отримаємо відповідь:

У посудині місткістю V = 6 л знаходиться при нормальних умовах двоатомний газ. Визначити теплоємність цього газу при постійному об'ємі.

2.25.

Дано

V = 6 л

= 5

= 10⁵ Па

= 273 К

= ?

Розв’язок.

Теплоємність речовини - це відношення кількості теплоти dQ, що поглинається нею у термодинамічному процесі, до зміни температури dT, що сталася за рахунок надання речовині цієї кількості теплоти:

. (1)

Питомою теплоємністю.

, (2)

Молярною теплоємністю називають кількість теплоти, яка потрібна для підвищення температури одного моля речовини на 1 К.

, (3)

де  - кількість молів речовини.

З рівняння (3) отримуємо

, (4)

Кількість молів речовини визначимо з рівняння стану ідеального газу (рівняння Менделєєва — Клапейрона):

, (5)

де =8,31 Дж/(моль•К) — універсальна газова стала.

Кількість молів речовини з рівняння (5) підставляємо у вираз (4)

, (6)

Молярні теплоємкості газу при ізохорному процесі дорівнює:

, (7)

Теплоємність з виразів (7) підставляємо у формулу (6) і отримаємо вираз для розрахунку:

= (8)

Підставляємо дані умови в рівняння (8) та отримаємо відповідь:

Визначити молярну масу газу, якщо різниця його питомих теплоємкостей = 2,08 кДж/(кг К).

2.26.

Дано

= 260 Дж/(кг∙К)

= ?

Розв’язок.

Між питомою і молярною теплоємністю існує співвідношення:

(1)

де - молярна маса речовини, моль/кг.

Молярні теплоємкості газу при ізобарному і ізохорному процесі пов’язані рівнянням Майора:

, (2)

де = 8,31 Дж/(моль∙К) – універсальна газова стала.

Тоді питомі теплоємності пов’язані таким чином:

. (3)

З рівняння (3) визначаємо молярну масу:

= (4)

Підставляємо дані умови в рівняння (4) і отримаємо відповідь:

2.27. Визначити молярну теплоємність газу, якщо його питома теплоємність = 10,4 кДж/(кг К) і = 14,6 кДж/(кг К).

2.27.

Дано

= 10,4 кДж/(кг∙К)

= 14,6 кДж/(кг∙К)

= ? = ?

Розв’язок.

Між питомою і молярною теплоємністю існує співвідношення:

(1)

де - молярна маса речовини, моль/кг.

Молярні теплоємкості газу при ізобарному і ізохорному процесі пов’язані рівнянням Майора:

, (2)

де = 8,31 Дж/(моль∙К) – універсальна газова стала.

Тоді питомі теплоємності пов’язані таким чином:

. (3)

З рівняння (3) визначаємо молярну масу газу:

= (4)

Тоді молярні теплоємності газу дорівнюватимуть

= (5)

= (6)

Підставляємо дані умови в рівняння (5) та (6) і отримаємо відповідь:

= =

Обчислити питому теплоємність газу, знаючи, що його молярна маса = 4 10^-3кг/моль і відношення теплоємкостей / = 1,67.

2.28.

Дано

= 4 10^-3кг/моль

/ = 1,67

= ? = ?

Розв’язок.

Між питомою і молярною теплоємністю існує співвідношення:

(1)

де - молярна маса речовини, моль/кг.

Відношення молярних теплоємкостей газу при ізобарному і ізохорному процесі дорівнює

. (2)

Тоді для даного газу дорівнює

. (3)

З рівняння (1) з урахуванням (3) визначаємо питомі теплоємності:

(4)

Підставляємо дані умови в рівняння (5) та (6) і отримаємо відповідь:

= =

Трьохатомний газ під тиском = 240 кПа і температурі t = 20°С займає об'єм V = 10 л. Визначити теплоємність цього газу при постійному тиску.

2.29.

Дано

= 6

= 240 кПа

t = 20°С

V = 10 л

= ?

Розв’язок.

. (1)

Молярна теплоємність при сталому тиску дорівнює

. (2)

Кількість молів речовини визначимо з рівняння стану ідеального газу (рівняння Менделєєва — Клапейрона):

, (3)

де = 8,31 Дж/(моль•К) — універсальна газова стала.

Підставляємо кількість молів газу з (3) та молярну теплоємність з (2) в рівняння (1) і отримаємо вираз для розрахунку відповіді:

= (4)

Дані умови задачі підставляємо у формулу (4) і отримаємо відповідь:

Одноатомний газ при нормальних умовах займає об'єм V = 5 л. Обчислити теплоємність Cv цього газу при постійному об'ємі.

2.30.

Дано

= 3

= 10⁵ Па

= 273 К

V = 5 л

= ?

Розв’язок.

. (1)

Молярна теплоємність при сталому об’ємові дорівнює

. (2)

Кількість молів речовини визначимо з рівняння стану ідеального газу (рівняння Менделєєва — Клапейрона):

, (3)

де = 8,31 Дж/(моль•К) — універсальна газова стала.

Підставляємо кількість молів газу з (3) і молярну теплоємність з виразу (2) у вираз (1) та отримаємо розрахункову формулу:

= (4)

Дані умови задачі підставляємо у формулу (4) і отримаємо відповідь:

Знайти середнє число зіткнень за час t = 1 с і довжину вільного пробігу молекули гелію, якщо газ знаходиться під тиском 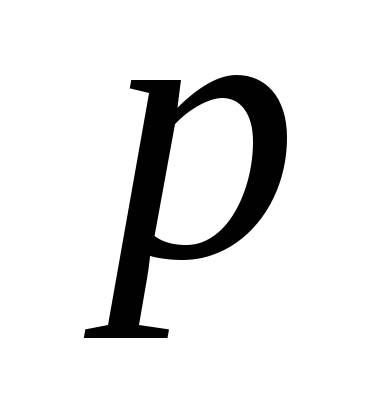= 2 кПа при температурі Т = 200 К.

2.31.

Дано

t = 1 с

= 2 кПа

Т = 200 К

= ? = ?

Розв’язок.

Середня кількість зіткнень однієї молекули за одиницю часу

. (1)

Середня довжина вільного пробігу молекул газу

, (2)

де — концентрація молекул, = 1,9∙10^-10 м — ефективний діаметр молекули гелію.

Середня арифметична швидкості молекул визначається формулою:

, (3)

де = 4 10^-3кг/моль – молярна маса гелію.

Концентрацію молекул газу визначимо з рівняння стану ідеального газу (рівняння Менделєєва — Клапейрона):

, (4)

де = 8,31 Дж/(моль•К) — універсальна газова стала; = 6,02∙10²³ моль^-1 – число Авогадро.

Концентрацію молекул газу з виразу (4) підставляємо в вираз (1) і отримаємо середню довжину вільного пробігу його молекул:

, (5)

Концентрацію молекул газу з виразу (4) та швидкість з виразу (3) підставляємо в вираз (2) і отримаємо середню кількість зіткнень однієї молекули за одиницю часу:

. (6)

Дані умови задачі підставляємо у формули (6) та (5) і отримаємо відповідь:

= =

Визначити середню довжину вільного пробігу молекули азоту в посудині місткістю V = 5 л. Маса газу m = 0,5 г.

2.32.

Дано

V = 5 л

m = 0,5 г

= 28 г/моль

d = 3∙10^-10 м

= ?

Розв’язок.

Середня довжина вільного пробігу молекул газу дорівнює

, (1)

де — концентрація молекул, — ефективний діаметр молекули газу.

Концентрацію молекул газу визначимо з рівняння:

, (2)

де = 6,02∙10²³ моль^-1 – число Авогадро; - кількість молів газу; - кількість молекул цього газу.

Підставляємо концентрацію молекул газу з (2) у формулу (1) і отримуємо розрахунковий вираз:

= (3)

Дані умови задачі (виражені в системі СІ) підставляємо у вираз (3) і отримаємо відповідь:

При нормальних умовах довжина вільного пробігу молекули водню дорівнює = 0,160 мкм. Визначити діаметр молекули водню.

2.33.

Дано

= 10⁵ Па

= 273 К

= 0,160 мкм

= 2 г/моль

d = ?

Розв’язок.

Середня довжина вільного пробігу молекул газу дорівнює

, (1)

де — концентрація молекул, — ефективний діаметр молекули газу.

Звідки отримаємо

. (2)

Концентрацію молекул газу визначимо з рівняння стану ідеального газу (рівняння Менделєєва — Клапейрона):

, (3)

де = 8,31 Дж/(моль•К) — універсальна газова стала; = 6,02∙10²³ моль^-1 – число Авогадро.

Підставляємо концентрацію молекул газу з (3) у формулу (2) і отримуємо розрахунковий вираз:

= (4)

Дані умови задачі (виражені в системі СІ) підставляємо у вираз (4) і отримаємо відповідь:

Кисень знаходиться під тиском = 133 нПа при температурі Т = 200 К. Обчислити середнє число зіткнень молекул кисню при цих умовах за одну секунду.

2.34.

Дано

t = 1 с

= 133 нПа

Т = 200 К

= 2,7∙10^-10 м

= 32 г/моль

= ? = ?

Розв’язок.

Середня кількість зіткнень однієї молекули за одиницю часу

. (1)

де — концентрація молекул, — ефективний діаметр молекули газу.

Середня арифметична швидкості молекул визначається формулою:

. (2)

Концентрацію молекул газу визначимо з рівняння стану ідеального газу (рівняння Менделєєва — Клапейрона):

, (3)

де = 8,31 Дж/(моль•К) — універсальна газова стала; = 6,02∙10²³ моль^-1 – число Авогадро.

Концентрацію молекул газу з виразу (3) та швидкість з виразу (2) підставляємо в вираз (1) і отримаємо середню кількість зіткнень однієї молекули за одиницю часу:

. (4)