8. Метод варіації довільних сталих

Вище ми застосовували метод підбору частинного розвязку при інтегруванні лінійних неоднорідних рівнянь

увипадку, якщо функціяf(x),що стоїть в правій частині, може бути представлена у вигляді:

або складається із суми такого роду функцій.

У всіх інших випадках користуються методом варіації довільних сталих. Розглянемо цей метод на рівняннях другого порядку.

а₀у + а₁у + а₂у=f (x) (1)

Суть цього метода полягає в тому, що для відповідного однорідного рівняння

а₀у + а₁у + а₂у= 0

записуємо загальний розвязок

у_одн= С₁у₁+ С₂у₂,

де С₁і С₂розглядаємо як функціїх.

Підбираємо їх так, щоб

у= С₁(х)у₁+ С₂(х)у₂

б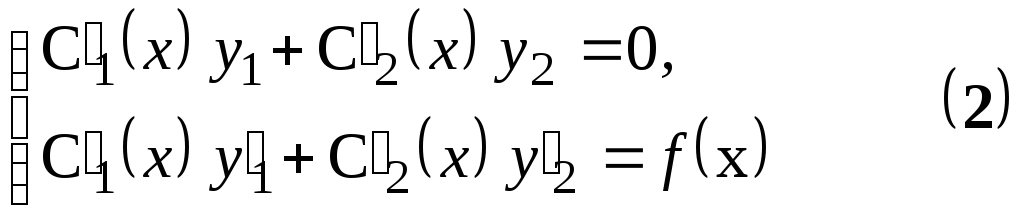уло розвязком рівняння (1). Невідомі функції С₁(х)i C₂(x) визначаються із системи рівнянь:

П р и к л а д 17. Розвязати рівняння: у+ у = .

Р о з в я з о к.Знайдемо загальний розвязок однорідного рівняння. Маємоу+ у= 0, його характеристичне рівнянняk²+1 = 0 іk₁= –і,k₂=і. Отже, загальний розвязок однорідного рівняння буде:

у_одн= С₁cosx +С₂sinx.

Так як права частина f(x) = не належить до функцій “спеціального вигляду”, розглянутих вище, і підібрати вигляд частинного розвязку по вигляду правої частини і кореням характеристичного рівняння в цьому випадку неможливо, то застосуємо метод варіації довільних сталих.

Загальний розвязок даного рівняння шукаємо у вигляді:

у= С₁(x) cosx +С₂ (x) sinx,

де С₁(x) і С₂ (x) невідомі функції від х.

Для їх знаходження складаємо систему:

Д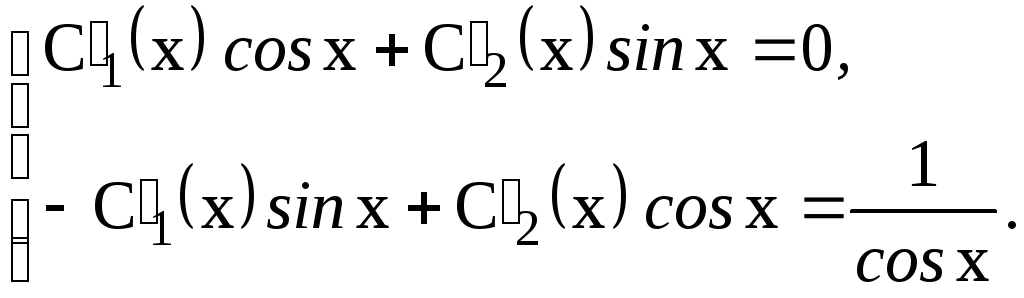омножаємо перше рівняння системи наsinx, а друге на cosx і додаємо одержані рівняння:

О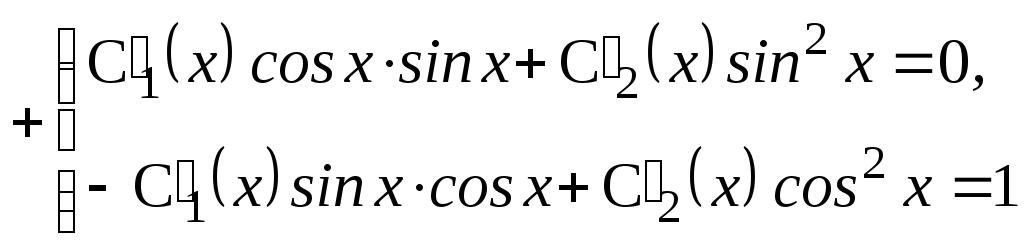держуємо:

С₂(х) = 1,

підставляючи С₂(х) в перше рівняння системи, знайдемо: С₁(х) = –tgx.

І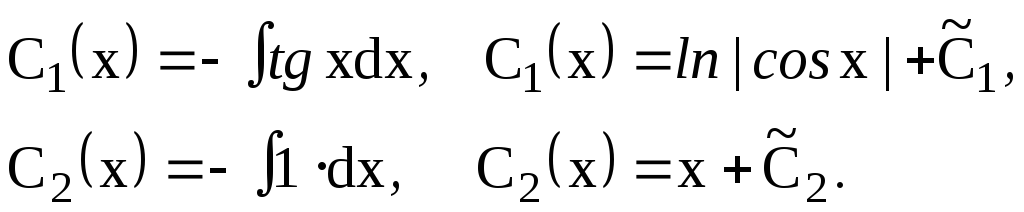нтегруванням знаходимо:

Загальний розвязок даного рівняння буде

П р и к л а д 18. Розвязати рівняння: у+ 4у + 4у = е^–2хlnx.

Р о з в я з о к.Корені характеристичного рівнянняk²+4k+ 4 = 0 дійсні і рівніk₁ =k₂= –2, отже, загальний розвязок однорідного рівняння буде:

у_одн= С₁е^–2х+ С₂хе^–2х.

Загальний розвязок неоднорідного рівняння знаходимо у вигляді:

у = С₁(x)е^–2х+ С₂(х)хе^–2х.

Так як для даного приклада у₁= е^–2х;у₂= хе^–2х;у₁= –2е^–2х;

у₂= е^–2х– 2хе^–2х, то згідно (2) маємо систему:

З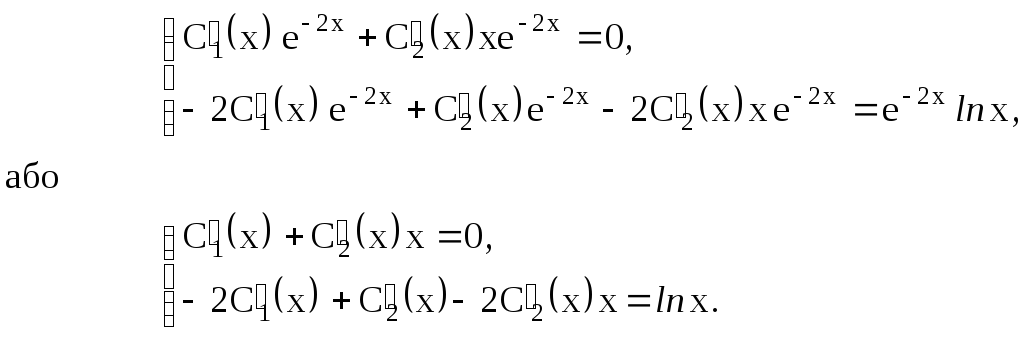цієї системи знайдемо функції С₁(x),С₂(х):

С₂(х) =lnx, С₁(x) = –xlnx.

І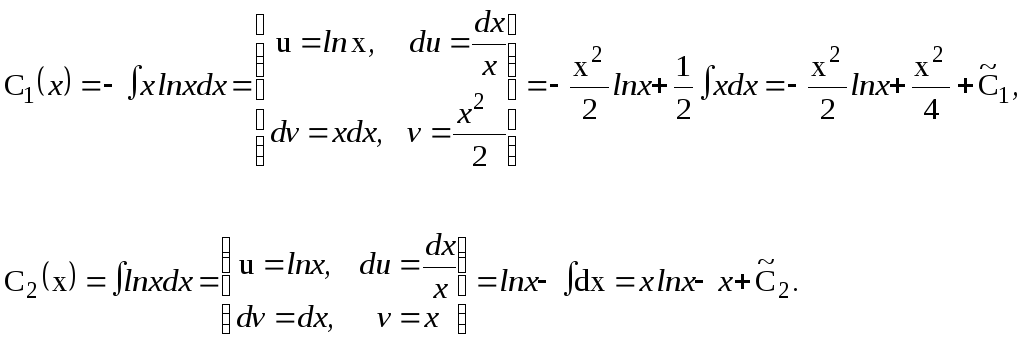нтегруючи, маємо:

Отже, загальний розвязок даного рівняння буде:



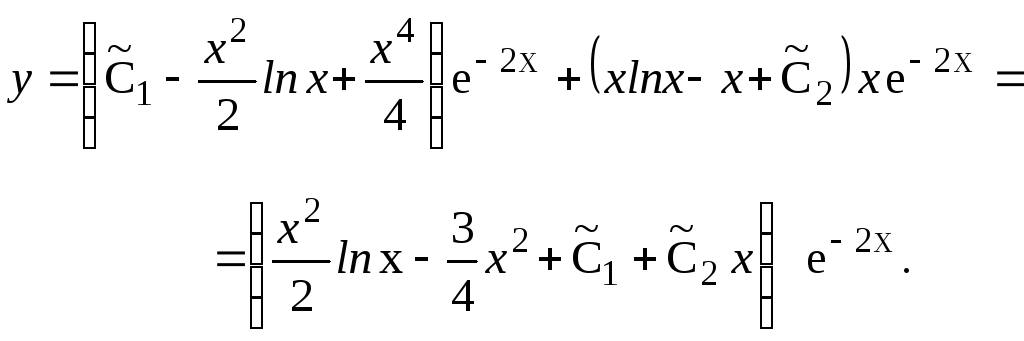
9. Системи лінійних диференціальних рівнянь першого порядку із сталими коефіцієнтами

Деякі технічні задачі приводять до розвязування системи двох або більше диференціальних рівнянь. Розглянемо системи диференціальних рівнянь першого порядка з двома невідомими функціями. Перехід до загального випадку не викликає яких-небудь принципових утруднень.

В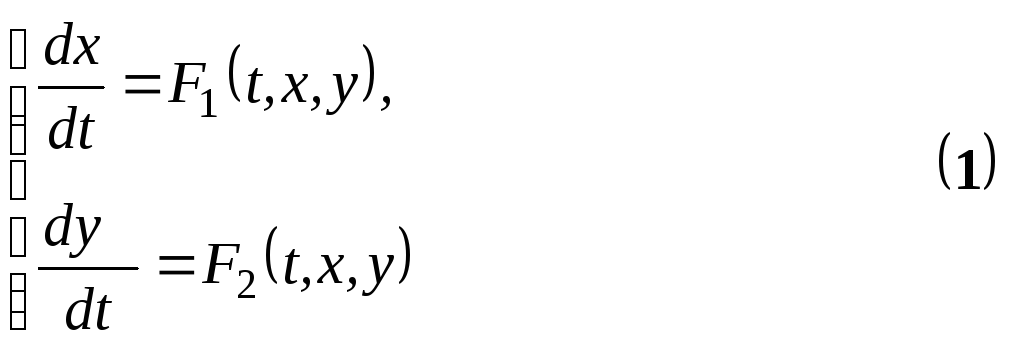нормальній формі система двох диференціальних рівнянь першого порядку має вигляд:

де t – аргумент,

х, у– шукані функції відt.

Розвязком системи(1) називається будь-який набір двох функцій:

х = x(t), y = y(t) (2)

що обертає обидва рівняння системи в тотожності. Задача Коши для системи (1) полягає у тому, щоб знайти такий розвязок (2), який при t = t₀приймав би задані значення:

х (t₀)=а, y(t₀) = b(3)

Загальний розвязок системи (1) містить дві довільні сталі С₁, С₂, фіксуючи які знаходять будь-який частинний розвязок у визначеній області зміни початкових умовt₀, a, b.

Метод розвязування систем із двох рівнянь першого порядку полягає в тому, що після диференціювання одного з рівнянь, систему зводимо до розвязку одного диференціального рівняння другого порядку відносно однієї невідомої функції.

П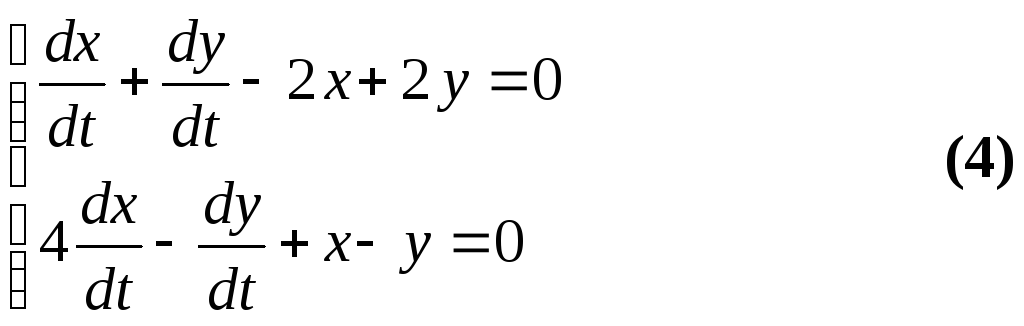р и к л а д 19. Знайти загальний розвязок системи диференціальних рівняннь

Р о з в я з о к.Спочатку систему (4), якщо можливо, приведемо до вигляду (1), тобто, до нормальної форми. Для цього потрібно по черзі виключити із рівнянь системи. Помножимо обидві частини першого рівняння на –4 і додавши до другого, виключимо. Потім, додаючи перше і друге рівняння, виключаємо. Одержимо:

З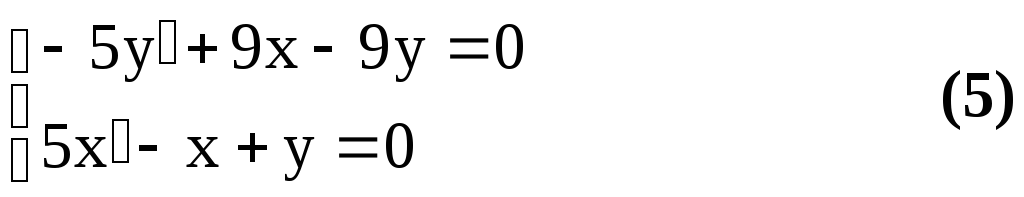найдемо, наприклад, із другого рівняння системи (5)у:

у =–5х+х(6)

знаходимо у= –5х+х і підставляємоуіув перше рівняння системи. Будемо мати:

25х– 5х+ 9х + 45х– 9х = 0, або 25х+ 40х= 0, або 5х+ 8х= 0

Розвязуючи ці рівняння, маємо його характеристичне рівняння

5k² + 8k= 0, звідсиk₁= 0,k₂= –8/5.

Загальний розвязок буде:

х= С₁+ С₂е^8/5t

П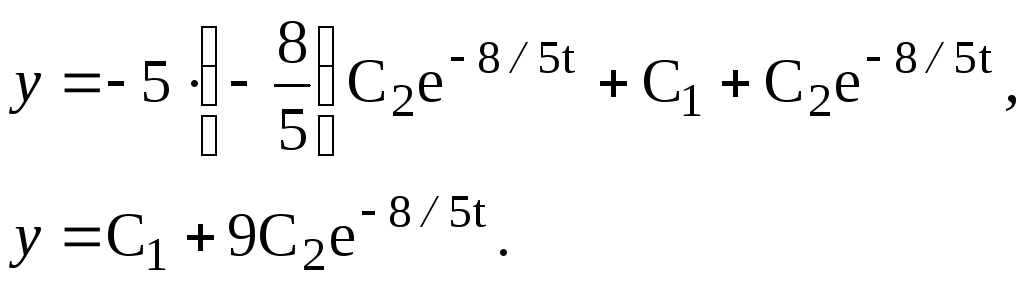родиференцюємо:х=8/5С₂е^{8/5 t}і підставимохіх в рівність (6), знайдемо другу невідому функціюу:

Отже, загальним розвязком системи будуть функції

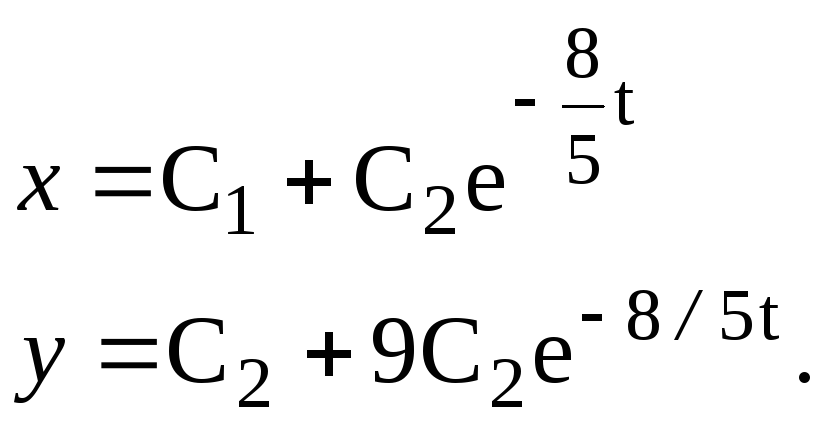
П р и к л а д 20. Знайти загальний розвязок системи

Р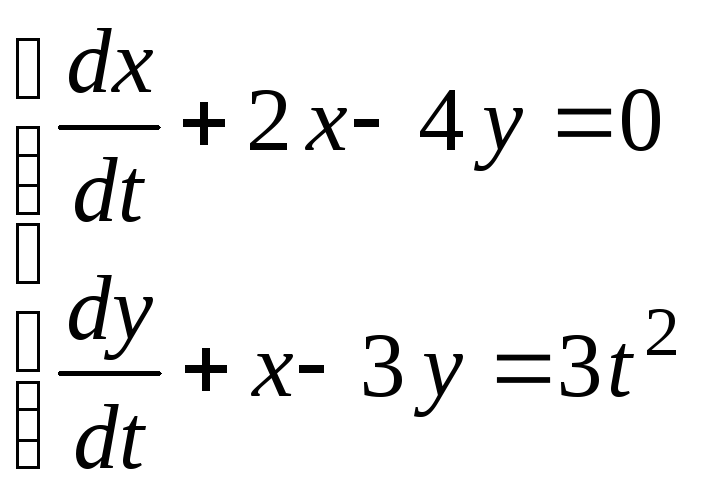о з в я з о к.. Диференцюємо поtперше рівняння:

х+ 2х  4у = 0,

потім виключаємо уіуз одержаного рівняння і двох даних рівнянь

у= 3t²  x + 3y;

4у = x + 2 x ,

в результаті одержимо одне диференціальне рівняння другого порядку з однією невідомою функцієй х:

х+ 2х  4(3t²  х + 3y) = 0,

х+ 2х  12t² +4 х  3х  6х = 0,

х 2х  2х= 12t² (7)

Розвязуємо його як лінійне неоднорідне рівняння зі сталими коефіцієнтами.

Характеристичне рівняння k²  k  2 = 0 має кореніk₁ = 2 k₂ = 1. Загальний розвязок однорідного рівняння буде:

х_одн= С₁е^2t + C₂e^t.

Частинний розвязокх_част. шукаємо у виглядіх_част. = Аt² + Bt + C.

Знаходимо х_част= 2At + B, х_част= 2A.

Підставляємо х_част,х_частіх_частв рівняння (7):

2А 2Аt B  2Аt²  2Bt  2C = 12 t².

Прирівнюючи коєфіцієнти при однакових степенях t лівої і правої частин останьої рівності, маємо:

О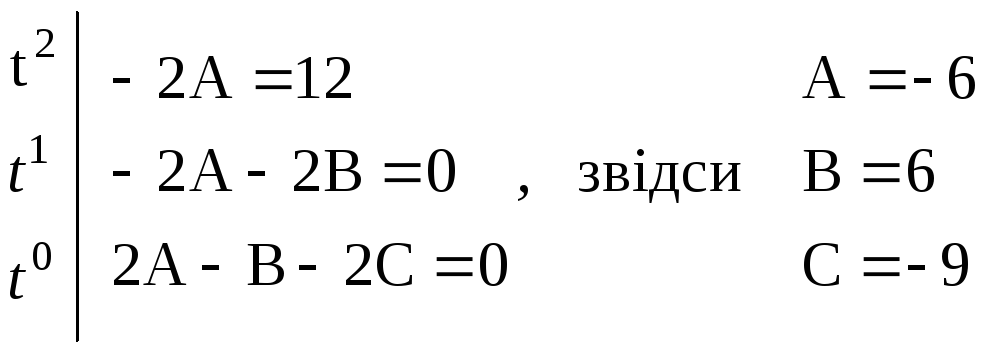тже,

х(t) =C₁e^2t+C₂e^-t6t²+ 6t9.

Другу невідому функцію у(t) знаходимо з першого рівняння системи, підставляючи в нього знайдене значеннях(1) і похідної

х(1) = 2С₁е^2t  С₂e^-t  12t + 6:

Т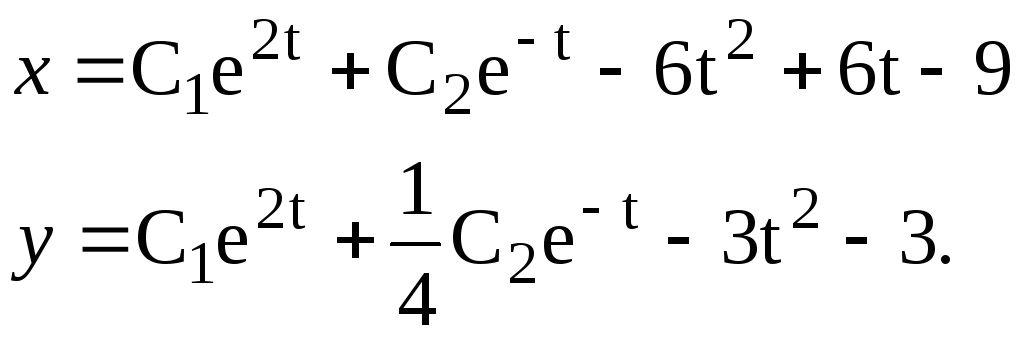аким чином, загальним розвязком даної системи буде сукупність знайдених функцій:

