5.Диференціальні рівняння, що допускають зниження порядку

І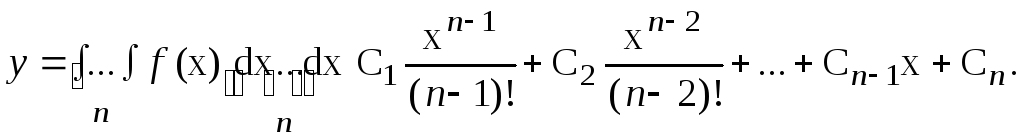. Рівняння виглядуу⁽ⁿ⁾ = f (x). Після n-кратного інтегрування одержуємо загальний розвязок

ІІ. Рівняння не містить шуканої функції та її похідних до порядку k-1 включно:

F (x, y^(k), y^(k+1),..., y⁽ⁿ⁾) = 0 (1)

Порядок такого рівняння можна знизити на k одиниць заміною y^(k) (х) = р(х). Тоді рівняння (1) набуває вигляду:

F (x, р, р,..., р^(n-k)) = 0

Із останнього рівняння, якщо це можливо, визначаємо р (x, C₁, C₂,...,C_n-k), а потім знаходимо у із рівняння y^(k) = f(x, C₁, C₂,..., C_n-k) k-кратним інтегруванням.

ІІІ. Рівняння не містить незалежну змінну:

F (y, у, у,..., y⁽ⁿ⁾) = 0.

П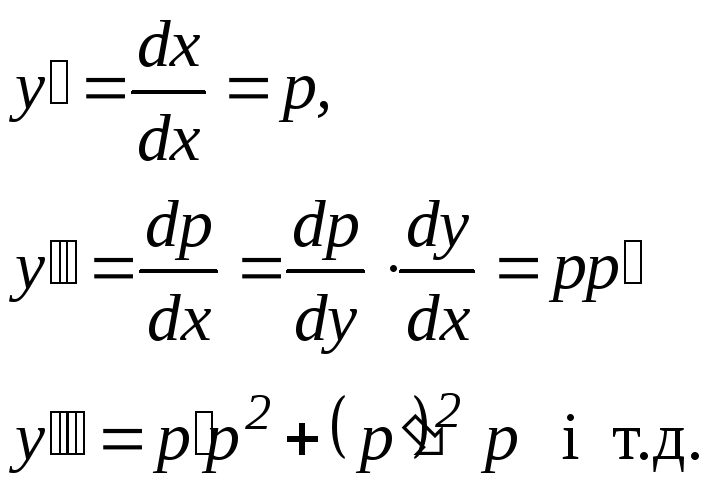ідстановкау = р дозволяє знизити порядок рівняння на одиницю. При цьому р розглядаємо як нову невідому функцію від у: р = р (у). Всі похідні у, у,..., у⁽ⁿ⁾ виражаються через похідні від нової невідомої функції р від у:

Підставляючи ці вирази замість у, у,..., у⁽ⁿ⁾ в рівняння, одержуємо диференціальне рівняння (n-1)-ого порядку.

П р и к л а д 8. Проінтегрувати рівняння у + уtgх = sin2x.

Р о з в я з о к. Це рівняння не містить у. Вводимо нову змінну y = z, y = z, одержимо: z + z tgх = sin2x.

Це лінійне диференціальне рівняння І порядку. Поклавши в ньому z = uv, z = uv + uv, маємо:

uv + uv + uv tgх = sin2x,

uv + u(v + v tgх) = sin2x,

Визначаємо v, поклавши v + vtgx = 0:

з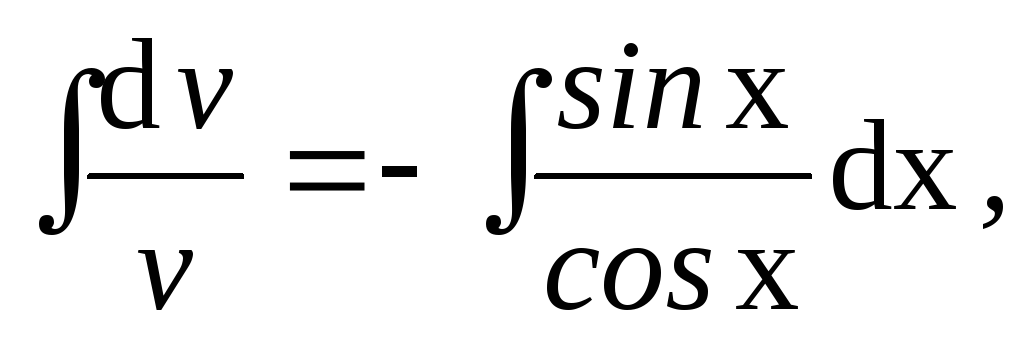відсиln|v| =  ln|cosx|, або v = cosx.

Визначаємо u(x):

ucosx = 2 sinx cosx, du = 2 sinx dx, u = 2 cosx + C₁.

Отже, z = (2 cosx + C₁) cosx, z = 2 cos² x + C₁ cosx.

П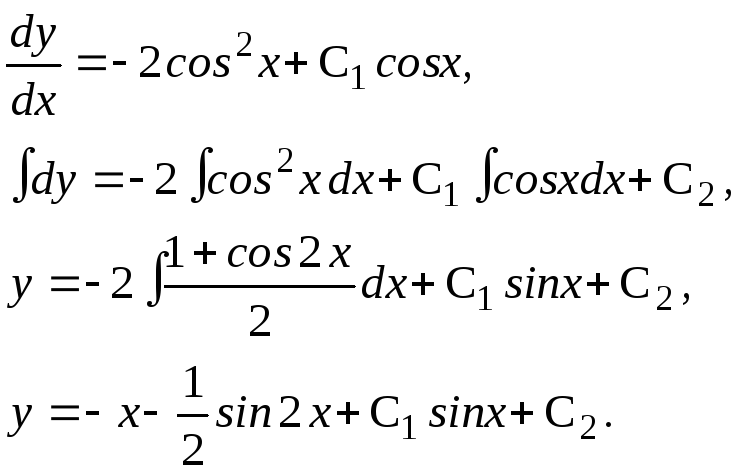овертаючись до змінноїу, одержимо:

Це і буде загальним розвязком даного диференціального рівняння.

П р и к л а д 9. Проінтегрувати диференціальне рівняння у = (у)².

Ро з в я з о к. Введемо нову функцію z = y, тоді одержимо рівняння першого порядку відносно невідомої функції z(x):

Відокремлюємо змінні і проінтегруємо:

Звідси

П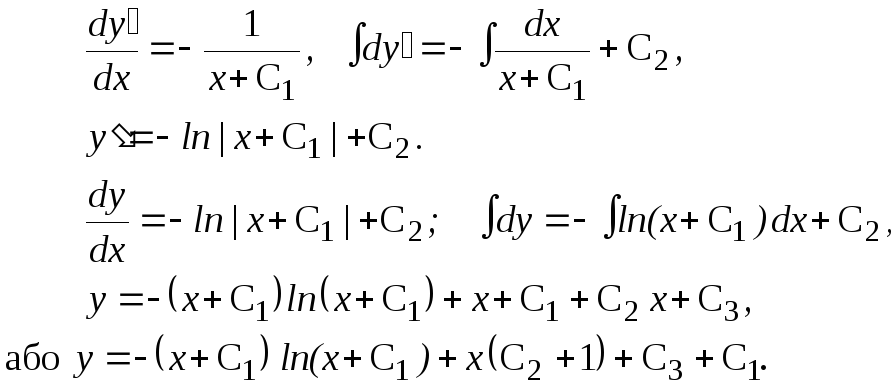ослідовно інтегруючи, маємо:

Замінивши С₂ + 1 на С₂, а С₃ + С₁ на С₃, одержуємо загальний розвязок:

y =  (x + C₁) ln (x + C₁) + C₂х + C₃.

П р и к л а д 10. Проінтегрувати рівняння 2(у)² = (у  1) y.

Р о з в я з о к. Поклавши в цьому рівнянні у = р, у =, одержимо диференціальне рівняння першого порядку:

Прирівнюючи перший множник до нуля, маємо:

Перевірка показує, що у = С (у = 0, у = 0) задовольняє дане рівняння, отже, є розвязком.

З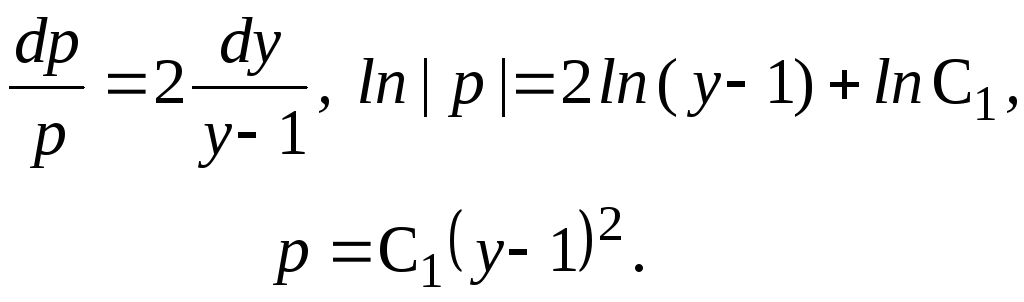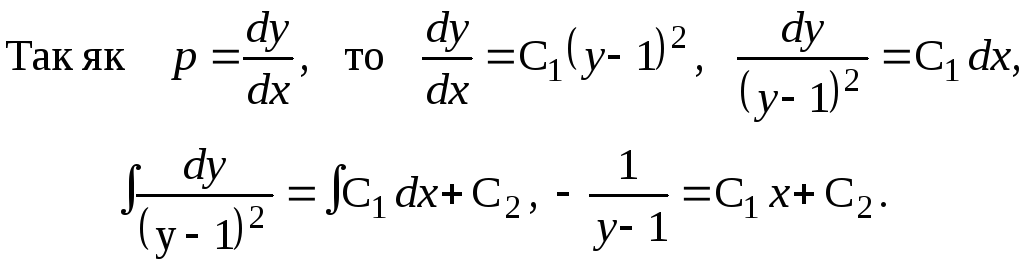агальний розвязок даного диференціального рівняння одержимо, проінтегрувавши рівняння з відокремлюваними змінними= 0:

Отже, загальний інтеграл має вигляд

(С₁х + С₂)(1  у) = 1.



6.Лінійні однорідні рівняння 2-го порядку

Рівняння вигляду

а₀у + а₁у + а₂у = 0 (1),

де а₀, а₁, а₂  сталі, називається лінійним однорідним рівнянням другого порядку із сталими коефіцієнтами.

ТЕОРЕМА. Якщоу₁(х) і у₂(х)  частинні розвязки рівняння а₀у + а₁у + а₂у = 0, причому їх відношення , тоу = С₁у₁(х) + С₂у₂(х) (2) є загальним розвязком цього рівняння.

Ці розвязки у₁(х) і у₂(х) знаходять у вигляді у = е^kx, де k  невизначене стале (дійсне або уявне). Для знаходження k складають характеристичне рівняння

a₀k² + a₁k + a₂ = 0 (3)

Зауважимо, що характеристичне рівняння складається з даного рівняння (1) шляхом заміни у,у,увідповідно наk²,k, 1.

Розвязуючи рівняння (3), знаходимо його кореніk₁іk₂. Можливі такі три випадки:

Таблиця 1

Корені рівняння (3)	Частинні розвязки (1)	Загальний розвязок (1)
1) Дійсні різні k1k2
2) Рівні k1=k2
3) Комплексні спряжені   і

П р и к л а д 11. Знайти загальні розвязки рівнянь: а) у – 2у–3у = 0;

б) у – 6 у +9 у = 0; в) 4 у  – 4 у +3 у = 0; г) у +25у = 0

Р о з в я з о к.

а)Запишемо характеристичне рівняння для даного диференціального:

k² – 2k –3 = 0.

Корені цього рівняння k₁= 3,k₂= –1 дійсні і різні, тому маємо (таблиця 1, формула 1):

у= С₁е^3х+ С₂е^–х.

б)Характеристичне рівнянняk²– 6k+ 9 = 0 має кореніk₁=k₂= 3 – дійсні і рівні, тому за формулою (2) табл. 1 маємо:

у= С₁е^3х+хС₂е^3х, або у = е^3х(С₁+хС₂).

в)Характеристичне рівняння 4k² – 4k + 3 = 0 має два уявних спряжених корені

Отже, за формулою (3) табл.1 загальний розвязок має вигляд:

г)Характеристичне рівнянняk²+ 25 = 0 має чисто уявні кореніk₁= 5iіk₂= –5i(= 0). Тому, згідно з формулою (3) табл.1 дістаємо:

у= С₁cos5x+ C₂sin5x.

П р и к л а д 12. Розвязати задачу Коши:

у – 6у + 5 у = 0, у (0) = 2, у (0) = 2.

Р о з в я з о к. Спочатку знаходимо загальний розвязок цього рівняння. Складаємо його характеристичне рівняння:k² – 6 k + 5 = 0; його кореніk₁= 1,k₂= 5, отже:

у= С₁е^х+ С₂е^5х.

Тепер використаємо початкові умови для знаходження С₁і С₂.

Підставляючи х= 0 іу= 2 у загальний розвязок, дістаємо: 2 = С₁е⁰+ С₂е⁰, або С₁+ С₂= 2.

Візьмемо похідну у від загального розвязку:

у= С₁е^х+ 5 е^5х,

підставляємо сюди значення х= 0 іу= –2. Маємо: –2 = С₁е⁰+ 5С₂е⁰,

або С₁+ 5С₂= –2.

Для визначення С₁і С₂потрібно розвязати систему рівнянь:

Р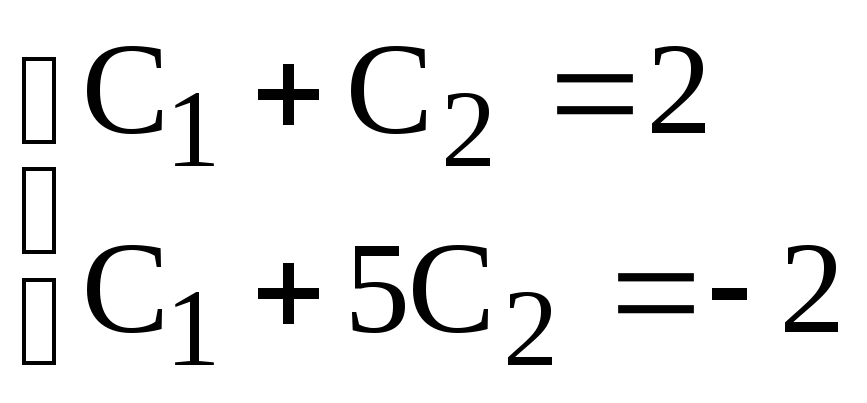озвязком цієї системи є С₁= –1 і С₂= 3. Підставляючи значення С₁і С₂у загальній розвязок, дістанемо шуканий частинний розвязок, тобто розвязок задачі Коши:

у= –е^х+ 3е^5х.

