Національна металургійна академія України

Криворізький металургійний факультет

Кафедра фундаментальних дисциплін

Вища математика

Розділ “Диференціальні рівняння ”

Методичні вказівки для практичних занять та самостійної роботи студентів спеціальності МЗ

дистанційна форма навчання

Затверджено

на засіданні кафедри фундаментальних

дисциплін

«_____»____________________ 2003 р.

Кривий Ріг

2003

Назва дисципліни: Вища математика

Методичні вказівки для практичних занять і самостійної роботи студентів

міжсесійний контроль № 6.

Розділ “Диференціальні рівняння ”

Укладач Рінейська Л.Ф., старший викладач

Рецензент Учитель О.Д., професор, докт.техн.наук

Компьютерний набір, верстка і макетування Васильєва О.А.

Посібник складено у відповідності з програмою вузівського курсу з вищої математики і містить приклади з диференціальних рівнянь, методичні вказівки з довідковим матеріалом для їх розвязання, задачі для самостійної роботи.

З М І С Т

1.Загальні відомості про диференіальні рівняння 5

2.Рівняння з відокремлюваними змінними 7

3.Однорідні рівняння 8

4.Лінійні рівняння 1-го порядку 10

5.Диференціальні рівняння, що допускають зниження порядку 13

6.Лінійні однорідні рівняння 2-го порядку 15

7. Лінійні неоднорідні рівняння 2-го порядку 17

8. Метод варіації довільних сталих 22

9. Системи лінійних диференціальних рівнянь першого порядку із сталими коефіцієнтами 24

10. Деякі задачі фізичного та геометричного змісту 27

1.Загальні відомості про диференіальні рівняння

Рівняння, що звязують незалежні змінні, шукану функцію і похідні або диференціали цієї функції, називаютьдиференціальними рівняннями.

Якщо невідома функція є функцією однієї змінної, то диференціальне рівняння називається звичайним.

Порядком диференціального рівняння називається порядок найвищого диференціалу, або похідної, що входять в диференціальне рівняння.

Диференціальне рівняння першого порядку має вигляд:

F (x, y, y) = 0 (1)

або y = f (x, y) (1a)

якщо воно розвязане відносно похідної.

Розвязком рівняння (1) або (1а) на інтервалі (а; b) називається диференційована на цьому інтервалі функція y =  (x), яка перетворює це рівняння в тотожність при всіх х  (а; b). Графік цієї функції називається інтегральною кривою заданого рівняння.

Загальним розвязком диференціального рівняння (1) або (1а) називається функція y =  (x, С), яка є розвязком цього рівняння при будь-яких допустимих значеннях сталої С, і для будь-якої початкової умови y(x₀ ) = у₀ існує єдине значення С = С₀, при якому розвязок y =  (x, С₀ ) задовольняє задану початкову умову.

Частинним розвязком називається будь-який розвязок y =  (x, С₀ ), який дістаємо з загального розвязку при конкретному значенні С = С₀.

Задача, в якій потрібно знайти частинний розвязок рівняння (1а), який задовольняє умову y(x₀ )= у₀, називається задачею Коши.

Загальному розвязку y =  (x ,С) на площині хОу відповідає сімя інтегральних кривих, залежних від одного параметра  довільної сталої С, а частинному розвязку, що задовольняє початкову умову y(x₀) = у₀  крива цієї сімї, що проходить через точку (х₀, у₀).

Якщо функція f і її похідна f_у в області D, то розвязок диференціального рівняння (1а) за умови y(x₀) = у₀ існує, і єдиний, тобто через точку (х₀, у₀) проходить єдина інтегральна крива даного рівняння (теорема Коши).

Диференціальне рівняння другого порядку має вигляд:

F (x, y, y) = 0 (2)

або y = f (x, y, у) (2a)

Задача Коши для рівняння (2а) формулюється так: знайти той розвязокy = (x), який задовольняє початкові умови

y (x₀)= у_0, y (x₀) = у₀ (3)

тобто треба знайти ту інтегральну криву, яка проходить через задану точку (х₀, у₀), і її дотична в цій точці має кутовий коефіциєнт у_0.

Загальним розвязком диференціального рівняння (2) або (2а) називається функціяy = (x, С₁, С₂ ), або Ф (x, y, C₁, C₂) = 0,яка задовольняє умовам:

1. вона перетворює рівняння в тотожність при довільних С₁, С₂;

2. при довільних початкових умовах (3) знайдуться такі С₁, і С₂, при яких початкові умови (3) будуть задовільнені.

Частинний розвязокодержується із загального при знаходженні певних значень С₁, і С₂за допомогою початкових умов (3).

П р и к л а д 1. Перевірити, що задана функція є розвязком відповідного диференціального рівняння:

а) y = 2e^3x, y  3 = 0

b) y = 4x + 3x², y 

Р о з в я з о к.

а)Знайдемо похіднуу= 6е^3хі підставимо її значення і значення самої функціїу= 2е^3ху задане рівняння. Дістанемо тотожність

6е^3х32е^3х0

б)Двічі диференцюючи задану функцію, дістаємоу= 4 + 6х іу= 6. Підставляючи значенняу, у іу в задане рівняння, маємо тотожність:

П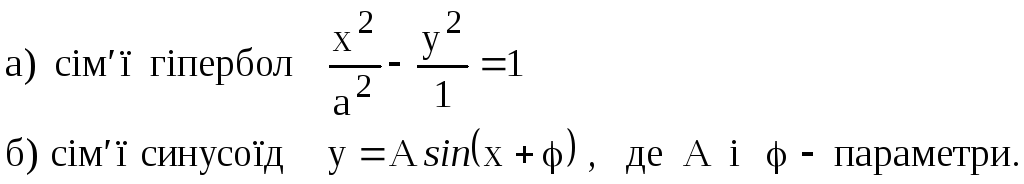р и к л а д 2.Методом виключення параметра скласти диференціальне рівняння:

Р о з в я з о к.

а)Диференцюючи це рівняння пох, одержимо

Помножимо обидві частини нах:

Підставляючи в рівняння сімї, знайдемо:

хуу  у²= 1.

б) Обчислимо

у= Аcos (x + ) i y =  A sin(x + ).

Звідси дістаємо

у = у, абоу + у= 0.

До прикладів 2170