
bludova_t_v_praktikum_z_vishoi_matematiki
.pdf
1
Візьмемо x3 1, тоді x1 1, x 2 1, X 2 1 .
1
3. 3 6 Маємо рівняння:
3 |
1 |
1 x |
|
|
0 |
||
|
1 |
1 |
1 |
|
|
0 |
|
|
1 x2 |
|
|
. |
|||
|
1 |
1 |
|
|
|
0 |
|
|
3 x3 |
|
|
|
|||
Знову шукаємо розв’язок системи в табличній формі:
х1 |
х2 |
х3 |
|
|
|
– 3 |
1 |
1 |
1 |
– 1 |
1 |
1 |
1 |
– 3 |
|
|
|
– 3 |
1 |
1 |
– 2 |
0 |
2 |
4 |
0 |
– 4 |
|
|
|
0 |
1 |
– 2 |
1 |
0 |
– 1 |
0 |
0 |
0 |
|
|
|
x 2 2x3, x1 x3.
|
|
|
|
|
1 |
|
Якщо x3 1, |
то x1 1, |
x 2 2 і |
X 3 |
|
2 |
|
|
. |
|||||
|
|
|
|
|
1 |
|
Ранг матриці
Розглянемо матрицю порядку m n . Виберемо в ній довільним чином k рядків та k стовпців. На їх перетині дістанемо визначник k-го порядку, який називається мінором k-го порядку даної матриці.
178

Рангом матриці називається найвищий порядок її мінора, відмінного від нуля.
Існує два методи обчислення рангу матриці. 1. Метод обвідних мінорів.
Якщо знайдений мінор k-го порядку матриці відмінний від нуля, а всі її мінори k 1-го порядку, які містять даний мінор k-го порядку, дорівнюють нулю, то ранг матриці дорівнює k .
2. Метод елементарних перетворень. Такими називають перетворення матриці:
1)переставлення рядків або стовпців матриці;
2)множення всіх елементів рядка або стовпця на відмінне від нуля число;
3)додавання до елементів деякого рядка або стовпця відповідних елементів іншого рядка або стовпця, помножених на відмінне від нуля число.
Елементарні перетворення не змінюють рангу матриці. За їх допомогою матрицю зводять до вигляду, коли в кожному рядку та кожному стовпці залишається не більш як одне відмінне від нуля число. Тоді ранг матриці дорівнює кількості відмінних від нуля елементів.
Задача 1.6. 1. Знайти ранг матриці
13 |
6 |
8 |
8 |
|
|
|
|
|
2 |
6 |
1 |
7 |
|
|
|
|
|
|
|
||||
|
7 |
12 |
5 |
|
. |
|
|
|
13 |
|
|
||||
|
3 |
2 |
2 |
2 |
|
|
|
|
|
|
|
||||
|
13 |
6 |
|
||||
Обчислимо мінор другого порядку: |
13 6 2 6 90. |
||||||
|
|
|
|
|
2 |
6 |
|
Обчислимо його обвідні мінори третього порядку:
13 |
6 |
8 |
|
|
|||
2 |
6 |
1 |
13 6 5 6 1 7 2 12 8 7 6 8 2 6 5 13 12 1 0; |
7 |
12 |
5 |
|
|
|
|
179 |

13 |
6 |
|
8 |
|
|
|
2 |
6 |
7 |
|
|
13 6 13 6 7 7 2 12 8 7 6 8 2 6 13 13 12 7 0; |
|
7 |
12 |
13 |
|
|
|
|
13 |
|
6 |
8 |
|
|
|
|
|
|||||
2 |
|
6 |
1 |
|
13 6 2 6 1 3 2 2 8 3 6 8 2 6 2 13 2 1 0; |
|
3 |
2 |
2 |
|
|
||
13 |
|
6 |
8 |
|
|
|
|
|
|||||
2 |
|
6 |
7 |
|
13 6 2 6 3 7 2 2 8 3 6 8 2 6 2 13 2 7 0. |
|
3 |
2 |
2 |
|
|
||
Таким чином, знайдено мінор другого порядку, відмінний від нуля, а всі його обвідні мінори третього порядку дорівнюють нулю. Тому ранг матриці дорівнює двом.
|
4 |
2 |
3 |
3 |
|
|
3 |
2 |
2 |
5 |
|
2. Знайти ранг матриці |
. |
||||
4 |
2 |
3 |
3 |
||
|
2 |
2 |
1 |
7 |
|
|
|
||||
Поміняємо місцями перший і четвертий рядки та перший і третій стовпці. Дістанемо еквівалентну матрицю
|
1 |
2 |
2 |
7 |
|
|
2 |
2 |
3 |
5 |
|
|
|
||||
|
3 |
2 |
4 |
|
. |
|
3 |
||||
|
3 |
2 |
4 |
|
|
|
3 |
||||
Помножимо елементи першого рядка на 2 та додамо до відповідних елементів другого рядка. Помножимо елементи першого рядка на 3 та додамо до відповідних елементів третього рядка. Помножимо елементи першого рядка на –3 та додамо до відповідних елементів четвертого рядка.
180
1 |
2 |
2 |
7 |
|
|
|
0 |
2 |
1 |
9 |
|
Дістанемо |
. |
||||
0 |
4 |
2 |
18 |
|
|
|
0 |
4 |
2 |
18 |
|
|
|
||||
Помножимо елементи першого стовпця на 2 та додамо до відповідних елементів другого стовпця. Помножимо елементи першого стовпця на – 2 та додамо до відповідних елементів третього стовпця. Помножимо елементи першого стовпця на – 7 та додамо
до відповідних елементів четвертого стовпця. Дістанемо еквівалентну матрицю
1 |
0 |
0 |
0 |
|
|
|
0 |
2 |
1 |
9 |
|
|
|
||||
|
0 |
4 |
2 |
18 |
. |
|
|
||||
|
0 |
4 |
2 |
18 |
|
|
|
||||
Помножимо елементи другого рядка на 2 та додамо до відповідних елементів третього рядка. Помножимо елементи другого рядка на –2 та додамо до відповідних елементів четвертого рядка.
1 |
0 |
0 |
0 |
|
|
|
0 |
2 |
1 |
9 |
|
Дістанемо еквівалентну матрицю |
. |
||||
0 |
0 |
0 |
0 |
|
|
|
0 |
0 |
0 |
0 |
|
|
|
||||
Поділимо елементи другого стовпця на 2. Утворений стовпець додамо до третього стовпця, потім помножимо його на 9 і додамо до четвертого стовпця.
1 |
0 |
0 |
0 |
|
|
|
0 |
1 |
0 |
0 |
|
Дістанемо еквівалентну матрицю |
. |
||||
0 |
0 |
0 |
0 |
|
|
|
0 |
0 |
0 |
0 |
|
|
|
||||
Ранг цієї матриці дорівнює 2.
181

Зведення квадратичної форми до канонічного вигляду
Квадратичною формою від п змінних називається вираз
n |
n |
a ji . З коефіцієнтів квадратичної фор- |
|
aij x i x j , в якому aij |
|
i 1 |
j 1 |
|
ми можна скласти симетричну матрицю A aij , яка назива-
ється матрицею квадратичної форми.
Кожну квадратичну форму в результаті певного перетворення координат можна звести до канонічного вигляду 1 y12 2 y22
n yn2 , при цьому 1 , 2 , , n називаються канонічними
коефіцієнтами квадратичної форми.
До канонічного вигляду квадратичну форму можна звести такими способами:
1. Метод Лагранжа.
Якщо a11 0 , групуємо доданки, що містять x 1 , та виділяємо повний квадрат. Потім групуємо доданки, що містять x 2 , та
виділяємо повний квадрат і т. д. 2. Метод Якобі.
Головними мінорами матриці квадратичної форми називаються мінори різних порядків, розташовані в її лівому верхньому куті:
|
|
|
|
|
|
|
|
|
a11 |
a12 |
|
, |
|
|
a11 |
a12 |
a13 |
|
, … . |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1 |
|
|
a |
|
, |
2 |
|
|
3 |
|
a |
21 |
a |
22 |
a |
23 |
|
||||
|
|
|||||||||||||||||||||
|
|
|
11 |
|
|
|
a21 |
a22 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a31 |
a32 |
a33 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Якщо всі головні мінори матриці квадратичної форми відмінні від нуля, то канонічні коефіцієнти квадратичної форми знаходять за формулами:
1 1 ; i |
i |
(i 2, 3, , n) . |
|
|
|||
|
|
||
|
i 1 |
|
3. Канонічні коефіцієнти квадратичної форми дорівнюють власним числам матриці квадратичної форми.
Задача 1.7. Звести квадратичну форму 3x12 4x 22 5x 32 + 4x1x2 4x2 x3 до канонічного вигляду.
1. За методом Лагранжа:
182

3x12 4x 22 5x 32 4x1x 2 4x 2 x 3 3 x12 43 x1x 2 4x 22
5x 32 4x 2 x 3 3 x1 23 x 2 2 83 x 22 4x 2 x 3 5x 32
|
|
|
2 |
|
|
|
2 |
|
8 |
2 |
|
3 |
|
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|
3(x1 |
|
|
|
x 2 ) |
|
|
|
x 2 |
|
|
x 2 x 3 |
|
5x 3 |
3 x1 |
|
|
x 2 |
|
|
||||||
3 |
|
3 |
2 |
3 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
8 |
|
|
3 |
|
|
|
2 |
|
7 2 |
|
|
|
2 |
|
8 2 |
|
7 2 |
|
|
|
|
|
||
|
3 x |
2 |
|
x |
3 |
|
|
2 x 3 |
3y1 |
|
|
3 y2 |
|
2 y3 . |
|
|
|
|
|
||||||
4 |
|
|
|
|
|
|
|
||||||||||||||||||
2. За методом Якобі:
3 |
2 |
0 |
|
|
Запишемо матрицю квадратичної форми A |
2 |
4 |
2 |
. |
|
0 |
2 |
5 |
|
Її головні мінори |
1 3; |
2 |
|
|
3 |
2 |
|
8; |
|
|
|
3 |
2 |
0 |
|
28 . |
|||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
3 |
|
|
2 |
4 2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
|
|
|
|
|
0 |
2 |
5 |
|
|
Канонічні коефіцієнти |
|
|
|
|
|
8 |
|
|
7 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
3; |
2 |
3 ; 3 |
2 . |
Тому квадратична |
||||||||||||||||||
форма |
зводиться |
до |
канонічного |
|
вигляду таким |
чином: |
|||||||||||||||||
3y 2 8 y 2 |
7 y 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
3 |
2 |
2 |
3 |
|
власні |
числа матриці |
квадратичної |
форми |
||||||||||||||
3. |
Обчислимо |
||||||||||||||||||||||
|
3 |
2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
4 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
. Для цього складемо характеристичне рівняння |
|||||||||||||||||||||
|
|
0 |
2 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3 |
2 |
|
0 |
0 . |
Розкриваючи визначник, дістанемо кубі- |
|||||||||||||||||
|
2 |
|
4 |
|
2 |
||||||||||||||||||
|
0 |
|
2 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чне рівняння |
3 |
12 2 39 28 0 , |
|
корені якого |
1 1; |
2 4; |
||||||||||||||||
3 7 . Таким чином, квадратичну форму можна звести до такого |
|||||||||||||||||||||||
канонічного вигляду: y12 4y22 |
7y32 . |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
183 |
|
|
|
|
|
|
|
|
|
|
|
||
Розділ 2. ВЕКТОРНА АЛГЕБРА. АНАЛІТИЧНА ГЕОМЕТРІЯ
Задача 2.1. Дано координати чотирьох вершин А1 (0, 0, 1), А2
(1, 0, – 1), А3 (1, 2, 0), А4 (2, 0, 1) піраміди А1А2А3А4. За допомогою методів векторної алгебри знайти:
а) довжину ребра А1А2; б) площу грані A1 A2 A3;
в) кут між векторами A1 A2 і A1 A4 ; г) об’єм піраміди A1 A2 A3 A4 ;
д) напрямні косинуси вектора а A1 A4 .
|
|
а) Розглянемо |
вектор |
|
|
|
|
|
|
|
|
1, |
0, |
2 . Довжину |
вектора |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
A1 A2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
x, y, z |
знаходимо за формулою |
|
|
|
|
|
|
|
x 2 x 2 |
x |
2 . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
a |
|
|
|
a |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
3 |
|
|
|
|
|
|
||||||
|
|
Звідси |
|
|
|
|
|
|
12 |
02 |
|
2 2 |
|
|
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
A A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
б) Площа |
|
|
грані |
A A A |
|
|
|
дорівнює |
S 1 |
|
|
|
|
|
|
|
|
|
|
, де |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
A A |
|
A A |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
2 |
1 |
3 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
— векторний добуток векторів |
|
|
|
|
|
і |
|
|
|
, який зна- |
||||||||||||||||||||||||||||||||||||||||||||||||
|
A1 A2 |
A1 A3 |
|
|
|
A1 A2 |
A1 A3 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ходимо за формулою |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
j |
k |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
y1 |
z1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 A2 |
A1 A3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
y2 |
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
У нашому випадку |
|
|
|
|
|
x1 , |
y1 , z1 1, |
0, 2 , |
|
|
x2 , y2 , z2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
A1 A2 |
A1 A3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1, 2, 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Маємо |
|
|
|
|
|
1 |
|
|
0 |
|
2 |
|
4i j 2k . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
A1 A2 |
A1 A3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Звідси SA A A |
1 |
42 12 |
22 |
|
|
13 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
2 |
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
в) Кут між векторами |
|
|
і |
|
|
|
|
знаходимо за формулою |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
A1 A2 |
A1 A4 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
A1 A2 |
A1 A4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
1 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
184

У нашому випадку |
|
1, 0, |
2 , |
|
|
|
|
2, 0, |
0 . |
||||||||
A1 A2 |
A1 A4 |
||||||||||||||||
Маємо: cos |
2 1 0 0 2 |
|
1 |
|
|
5 |
. |
|
|||||||||
|
|
|
|
5 |
|
5 |
|
||||||||||
|
|
|
|
5 2 |
|
|
|
|
|
|
|
|
|
||||
Отже, arccos |
5 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
г) Об’єм піраміди знаходимо за формулою |
|
||||||||||||||||
|
|
|
|
V 1 |
|
x1 |
y1 |
z1 |
|
, |
|
|
|||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
x2 |
y2 |
z2 |
|
|
|
|||||||
6 |
|
x3 |
y3 |
z3 |
|
|
|
|
|
||||||||
де A1 A2 x1, y1, z1 , A1 A3 x2 , y2 , z2 , A1 A4 x3 , y3 , z3 . Використовую-
чи попередні обчислення, дістаємо
V |
1 |
|
1 |
0 |
2 |
|
|
1 |
8 |
4 |
куб |
од. . . |
|
|
|||||||||||
|
1 |
2 |
1 |
|
||||||||
6 |
|
|
6 |
3 |
||||||||
|
|
2 |
0 |
0 |
|
|
|
|
|
д) Застосовуючи формулу напрямних косинусів
cos |
|
|
x |
|
, |
cos |
|
|
y |
|
, cos |
|
|
z |
|
, |
|
|
a |
|
|
|
a |
|
|
|
a |
|
|||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
знаходимо cos 22 1; cos 02 0; cos 02 0.
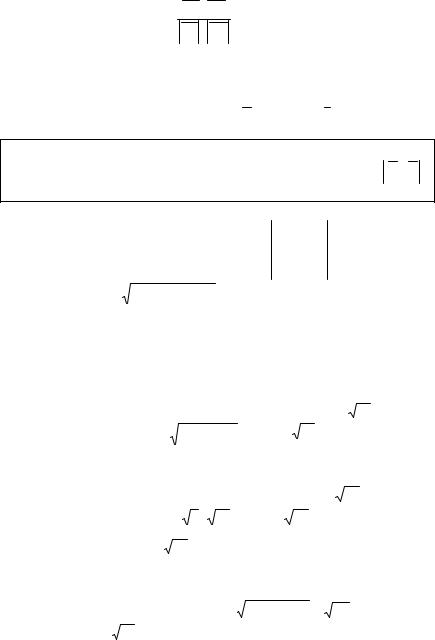
Задача 2.1-1. Дано довжину ОА = 1, ОВ = 2, ОС = 3 ребер ОА, ОВ, ОС прямокутного паралелепіпеда.
ЕТ
С |
|
|
|
c |
n |
|
|
B |
|
||
|
D |
||
b |
m |
||
|
|||
O |
a |
A |
|
|
Знайти:
а) площу трикутника ОЕD; б) проекцію вектора АВ на ВС;
185
в) кут АВС; cos ABC BA BC ; BA BC
г) довжину діагоналі паралелепіпеда; д) об’єм піраміди ОАВС.
а) Діагоналі ОD і ОЕ розглянемо як вектори m i n . У координатній формі вони запишуться як m 1, 2, 0 , n 0, 2, 3 .
Площу трикутника ОЕD знаходимо за формулою SOED 12 m n .
|
|
|
|
i |
j |
k |
|
Обчислимо векторний добуток |
|
|
|
1 |
2 |
0 |
6i 3 j 2k. |
m |
n |
||||||
0 |
2 |
3 |
|
||||
Звідси SOED 12 |
|
|
|
|
62 3 2 22 |
72 (кв. од.). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
б) |
пр |
|
|
|
|
|
|
|
|
|
|
АВ |
ВС |
. |
|
|
|
У нашому |
випадку |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
АВ |
|
|
|
|
|
|
АВ |
а |
b |
|||||||||||||||||||||||||||||||||||||||||||
ВС |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ВС |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1, 2, 0 , |
|
|
|
|
|
|
|
|
|
|
|
0, 2, 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
BC |
b |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Маємо: пр |
|
|
|
|
|
|
|
|
|
1 0 2 2 3 0 |
|
|
4 |
|
|
4 13 |
. |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
АВ |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ВС |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
32 |
|
13 |
|
|
13 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
в) Оскільки |
|
1, 2, |
|
0 , |
|
|
|
0, 2, |
3 , дістанемо: |
||||||||||||||||||||||||||||||||||||||||||||||||
BA |
|
BC |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
cos ABC 1 0 2 2 0 3 |
|
4 |
|
|
4 |
65 |
. |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
65 |
|
|
65 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Отже, ABC arccos |
4 |
65 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
65 |
|
1, |
|
2, 3 . Довжиною діагоналі пара- |
|||||||||||||||||||||||
г) Розглянемо вектор |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
OT |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
лелепіпеда є довжина вектора |
|
12 22 |
32 |
14. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
OT |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Звідси |
|
|
|
|
|
|
|
|
14. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
ОТ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
186

|
|
д) Об’єм піраміди знаходимоза формулою V |
1 |
|
|
|
|
|
OC, |
|||||||||||||||||||||
OA |
OB |
|||||||||||||||||||||||||||||
де |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
1, 0, 0 , |
||||||
OA |
|
OB |
OC |
|
|
|
|
— мішаний добуток |
векторів |
|
OA |
|||||||||||||||||||
|
|
|
0, 2, |
0 , |
|
|
|
0, |
0, |
3 . |
|
|
|
|
|
|
|
|
|
|||||||||||
OB |
OC |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
Маємо: V |
1 |
|
|
1 |
0 |
0 |
|
1 2 3 1 (куб. од.). |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
0 |
2 |
0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
0 |
0 |
3 |
|
6 |
|
|
|
|
|
|
|
|
|
||
|
|
Задача |
2.1-2 |
|
|
Дано три послідовні вершини |
паралелограма |
|||||||||||||||||||||||
А (1, 0, 0), В (4, 3, 2), С (2, –1, 0). Застосовуючи методи векторної |
||||||||||||||||||||||||||||||
алгебри, знайти: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
а) координати четвертої вершини D (x, y, z); |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
б) площу трикутника АВС; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
в) довжину діагоналі АС; |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
г) кут АВС; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
д) об’єм піраміди ОАВС. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
а) Cторони паралелограма розглядаємо як вектори. Маємо: |
||||||||||||||||||||||||||||
|
|
|
|
, |
AB |
4 1, 3 0, 2 0 3, 3, 2 , |
DC 2 x, 1 y, z . |
|||||||||||||||||||||||
|
AB |
DC |
||||||||||||||||||||||||||||
Вектори рівні, якщо рівні їхні координати. Звідси дістаємо:
3 2 x, |
x 1, |
|
|
1 y, |
|
3 |
y 4, |
|
|
z, |
|
2 |
z 2. |
|
Отже, D (– 1, – 4, – 2).
б) Площа АВС є половина площі паралелограма, побудованого на векторах BA i BC ; площа його дорівнює модулю вектор-
BA i BC.
Маємо: |
|
3, 3, 2 , |
|
2, 4, 2 . |
BA |
BC |
Векторний добуток BA BC знаходимо за формулою:
|
|
|
|
i |
|
j |
|
|
k |
|
|
|
|
|
|
|
|
|
|
3 |
3 |
2 |
2i 2 |
|
6 |
|
. |
||||
BA |
BC |
j |
k |
||||||||||||
|
|
|
|
2 |
4 |
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
187
