
дискретна+математика_09
.pdfОтримані комбінації задовольняють різним умовам. Залежно від правил їх утворення можна виділити три типи
комбінацій: перестановки, розміщення, сполучення.
Розглянемо їх окремо.
7.1. Перестановки
Визначення 7.1. Комбінації з n елементів, які відрізняються друг від друга тільки порядком елементів,
називаються перестановками.
Перестановки позначаються символом Рn, де n — число елементів, що входять у кожну перестановку.
Приклад 7.1. Нехай множина М містить три букви А, В, С. Складемо всі можливі комбінації із цих букв: АВС, АСВ, ВСА, CAB, CBA, ВАС (усього 6 комбінацій). Видно, що вони відрізняються друг від друга тільки порядком розташування букв.
Дійсно, на перше місце в комбінації (перестановці) можна поставити три букви. На друге місце вже можна поставити тільки дві букви із трьох (одна посіла перше місце), а на третьому виявиться тільки одна (та, що залишилася).
Виходить, 3 · 2 · 1 = 6 = P , але 1 · 2 · 3 = 3! Прийшли до
3
відомого у математиці поняттю факторіала.
Визначення 7.2. Добуток всіх натуральних чисел від 1 до n включно називають n-факторіалом і пишуть: n!= 1 · 2 · 3 ·
... · (n - 1) · n. Вважають, що 0! = 1 і |
n N . Основна |
властивість факторіала: (n + 1)! = (n +1) n!. |
|
Отже, число перестановок обчислюємо за формулою: |
|
Рn = n! |
(7.1) |
91 |
|

7.2. Розміщення
Визначення 7.3. Комбінації з n елементів по m елементів, які відрізняються друг від друга або самими елементами або порядком елементів, називаються
розміщеннями.
Розміщення позначаються символом À nm , де n - число
всіх наявних елементів, m - число елементів у кожній комбінації. Число розміщень можна обчислити по формулі:
À nm = n(n -1)(n - 2)...(n - m +1), де 0 ≤ m ≤ n; m, n N. (7.2)
Вважають, що À n0 =1 .
Приклад 7.2. Нехай множина M містить чотири букви А, В, С, D. Склавши всі комбінації тільки із двох букв, одержимо:
АВ, AC, AD, ВА, ВР, BD, СА, СВ, CD, DA, DB, DC.
Бачимо, що всі отримані комбінації (їх 12) відрізняються або буквами, або їхнім порядком (комбінації ВА і АВ вважаються різними).
За формулою (7.2) À 42 = 4 ×3 = 12 , що збігається з
результатом наведеного приклада. Тут кожен рядок відповідає однієї із всіх наявних букв (n=4), а число стовпців відповідає іншим буквам (n-1=3) , усього 4 · 3=12 різних комбінацій.
Формулу (7.2) можна записати у факторіальній формі:
|
À |
nm = |
n! |
|
|
|
(n - m)! |
. |
(7.3) |
||
|
Основні властивості розміщень: |
|
|||
1) À m+1 |
= Am ×(n - m); |
|
|
2) À n = P = n!. |
|
n |
n |
|
|
n |
n |
|
|
92 |
|
|
|

7.3. Сполучення
Визначення 7.4. Сполученнями називаються всі можливі комбінації з n елементів по m, які відрізняються друг від друга принаймні хоча б одним елементом ( m, n N і n ³
m).
У загальному випадку число сполучень із n елементів по m дорівнює числу розміщень з n елементів по m, діленому на
m
число перестановок з m елементів: Ñ nm = An . Використовуючи
Pm
для чисел розміщень і перестановок факторіальні формули
À |
nm = |
m! |
|
і Pn |
= n!, одержимо формулу числа сполучень у |
|||||||
(m - n)! |
||||||||||||
вигляді: |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Cnm = |
n! |
|
|||
|
|
|
|
|
|
|
(n - m)!m! |
. |
(7.4) |
|||
|
|
Основні властивості сполучень: |
|
|||||||||
|
|
n−m |
= |
|
Pn |
= |
n! |
|
||||
|
1) Cn |
|
|
|
(n - m)!m! |
; |
|
|||||
|
|
P |
× P |
|
||||||||
|
|
|
|
|
n−m |
m |
|
|
|
|
|
|
2) Cnm = Cnn−m .
Приклад 7.3. Множина М утворена з чотирьох букв А, В, С, D. Скласти комбінації з двох букв, що відрізняються друг від друга хоча б одним елементом.
Маємо АВ, AC, AD, ВР, BD, CD. Виходить, що число сполучень з чотирьох елементів по двоє дорівнює 6. Це коротко
записується так: Ñ 42 = 6 .
93

7.4. Розміщення з повтореннями
Розміщення з n елементів по k зображують упорядковані комбінації різних елементів множини М, |М|= n. Часто доводиться робити упорядковані комбінації з повтореннями деяких елементів. Наприклад, з множини М = {A, Б} можна зробити вісім комбінацій з трьох елементів: ААА, ААБ, АБА, БАА, БАБ, ББА, АББ, БББ. Тут n = 2, k = 3. Такі упорядковані k- комбінації називають кортежами довжини k. Два кортежі (тобто дві загальні комбінації) вважаються однаковими, якщо вони мають однакову довжину і на місцях з однаковими номерами стоять однакові елементи.
Визначення 7.5. Розміщенням з повтореннями з n
елементів по k називається кортеж довжини k з n елементів.
Кількість кортежів обчислюється за формулою: |
|
||
|
|
= nk . |
|
|
Аk |
(7.5) |
|
|
n |
|
|
Розглянутий вище приклад обчислюється за формулою (7.5)
А23 = 23 = 8 .
Дійсно, після заповнення першого місця кортежу довжиною k одним з n елементів (що можливо зробити n варіантами) заповнити друге місце кортежу можна знову будьяким елементом з усієї множини (повторюючи в одному з варіантів елемент, який знаходиться на першому місці), і так далі k разів. За правилом добутку одержимо, що
















 .
.
94

8. ЗРАЗОК ВИКОНАННЯ КОНТРОЛЬНОЇ РОБОТИ
Завдання 1. Задати різними способами елементи множини букв у слові «СВЯТО». Знайти потужність множини і булеана множини.
Розв’язання: Задамо множину
а) перерахуванням: 












 ;
;
б) описом характеристичної властивості:

































 .
.
За визначенням 1.2 потужність множини 




 . За визначенням 1.6 потужність булана
. За визначенням 1.6 потужність булана 



















 .
.
Завдання |
2. |
|
|
|
Задано |
|
множини |
||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Визначити наступні множини: |
|
|
. |
||||||||
Розв’язання: За визначеннями 1.7 – 1.11 маємо
; |
|
; |
|

























































 .
.
Завдання 3. Для наведеної множини 






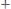



 побудувати діаграму Венна, на якій штриховкою показати область, що зображує множину.
побудувати діаграму Венна, на якій штриховкою показати область, що зображує множину.
Розв’язання: Побудуємо спочатку множину 



 , а потім шукану множину
, а потім шукану множину 










 :
:
95
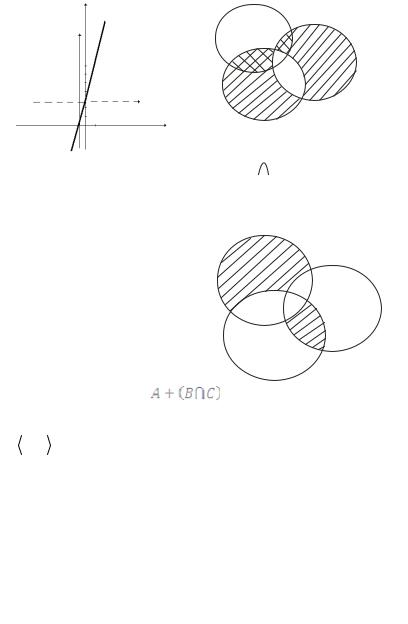
A |
A |
C |
C |
B |
B |
B+C |
A (B+C) |
Завдання 4. За допомогою операцій над множинами описати A множини, що відповідають зафарбованій частині діаграми Венна:
Розв’язання: Скориста-
ємося приведеними у розділі 1.3 рис. 1.2, маємо:
|
|
|
|
|
B |
|
|
|
|
|
. |
Завдання |
5. |
З’ясувати, |
чи |
||
f = { x, y |
|
y = 4x + 3, |
x, y R} функцією. |
||
|
|||||
властивість. Якщо функція є взаємнооднозначною, знайти обернену.
Розв’язання: Побудуємо графік відношення. Дане відношення є функцією, тому що не існує елементів, які мають однакові перші координати. Ця функція є взаємно однозначною, тому що переводить
C
є відношення Визначити її
96

різні елементи в різні. Знайдемо функцію, обернену до даної:
f = { x, y |
|
y = 4x + 3, x, y R}; |
||||
|
||||||
f −1 = { y, x |
|
|
x = 4 y + 3, |
x, y R}; |
||
|
||||||
f −1 = { y, x |
|
|
4 y = x − 3, |
x, y R}; |
||
|
|
|||||
f −1 = y, x |
|
y = |
x |
− |
3 |
; |
x, y R . |
|
|
||||||
|
|
|
4 4 |
|
|
||
|
|
||||||
Завдання 6. Знайти істинносте значення наступного |
|||||||
висловлювання: |
|
P Q →~ ((Q ~ R) → (Q P)), якщо |
|||||
P = 1 , Q = 0 , R = 1 .
Розв’язання: Скористаємося таблицями істинності, які приведені у розділі 3.1:
P Q →~ ((Q ~ R) → (Q P))
1 |
0 |
0 |
1 |
0 |
1 |
|
|
|
0 |
|
|
|
|
|
0 |
|
0 |
1
0
0
1
Отже, дане висловлення істинне.
Завдання 7. Скласти таблицю істинності для наступного висловлювання: 























 .
.
Розв’язання: Скористаємося таблицями істинності, які приведені у розділі 3.1 і виконаємо всі дії послідовно:
97

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
|
0 |
|
|
1 |
1 |
|
|
0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
|
1 |
|
|
0 |
0 |
|
|
0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
|
0 |
|
|
1 |
1 |
|
|
0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
0 |
|
0 |
|
|
1 |
1 |
|
|
0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
1 |
|
0 |
|
|
1 |
1 |
|
|
0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
|
1 |
|
|
0 |
1 |
|
|
1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
0 |
|
0 |
|
|
1 |
1 |
|
|
0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
|
0 |
|
|
1 |
1 |
|
|
0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Завдання 8. Обчислити значення функції
























 на зазначеному наборі змінних:
на зазначеному наборі змінних: 







 .
.
Розв’язання: Скористаємося таблицями 4.1, 4.2:

















 ;
;








 .
.
Отже, функція на зазначеному наборі змінних хибна.
98

Завдання |
9. |
Логічну |
функцію |



























 представити булевою формулою у вигляді ДДНФ і у вигляді ДКНФ:
представити булевою формулою у вигляді ДДНФ і у вигляді ДКНФ:
Розв’язання: Побудуємо таблицю істинності функції за допомогою таблиць 4.1, 4.2:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
0 |
|
|
|
1 |
|
|
0 |
|
|
0 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
0 |
|
|
|
1 |
|
|
0 |
|
|
0 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
0 |
|
|
|
1 |
|
|
0 |
|
|
0 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
1 |
0 |
|
|
|
1 |
|
|
0 |
|
|
0 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
1 |
|
|
|
0 |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
0 |
0 |
|
|
|
0 |
|
|
1 |
|
|
0 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
0 |
1 |
|
|
|
1 |
|
|
0 |
|
|
0 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
0 |
|
|
|
1 |
|
|
0 |
|
|
0 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Скористаємося наслідками 1,2 до теореми 4.1 та запишемо ДДНФ та ДКНФ.
Бачимо, що функція має лише один одиничний набір змінних, тому ДДНФ буде мати одну диз’юнкцію кон’юкцій. Зауважимо, що змінні, які дорівнюють одиниці беремо без заперечення, а змінні, які дорівнюють нулю – із запереченням. Отже, ДДНФ функції має вигляд:


















 .
.
Функція має сім нульових набрів змінних, тому ДКНФ буде мати сім кон’юкцій диз’юнкцій. Зауважимо, що змінні, які
99
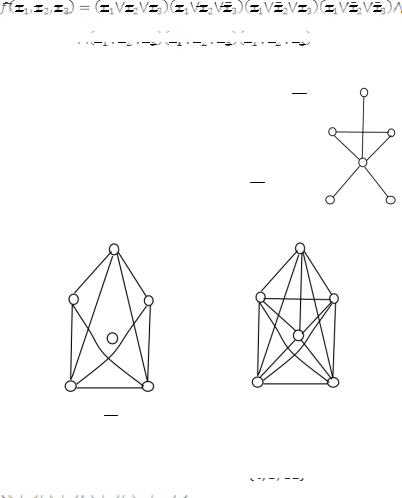
дорівнюють одиниці беремо із запереченням, а змінні, які дорівнюють нулю – без заперечення. Отже, ДКНФ функції має вигляд:








































 .
.
Завдання 10. Визначити доповнення G
графа G . Побудувати повний граф, якщо G має вигляд:
Розв’язання: Скористаємося визначеннями 5.7, 5.8. Побудуємо доповнення G графу G . Отже повний граф має вигляд:
G G
Завдання 11. Для неорієнтованого графу G виконати операції видалення вершин 







 та ребер
та ребер 











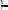




















 . Побудувати отриманий граф.
. Побудувати отриманий граф.
100
