- •Кафедра фізики в.В.Соловйов, л.П.Давиденко Конспект лекцій із фізики
- •Полтава 2004
- •Тема: елементи кінематики
- •Лекція іі тема: динаміка частинок план
- •Лекція ііі тема: закони збереження. Тверде тіло план
- •Повний імпульс ізольованої (замкненої) механічної системи не змінюється при будь-яких взаємодіях у ній.
- •Трохи про консервативні системи
- •Швидкість зміни момента імпульсу відносно нерухомої точки о дорівнює результуючому моменту сил усіх зовнішніх сил.
- •Лекція IV тема: механічні коливання
- •Лекція V тема: механічні хвилі
- •Лекція vі тема : елементи механiки суцiльних середовищ
- •Лекція VII тема: макроскопічний стан
- •Лекція viiі тема: статистичний розподіл. Явища переносу
- •Лекція IX тема: основи термодинаміки
- •Лекція X тема: тверді тіла та рідини
- •Лекція XI тема: електростатика план
- •Механізм взаємодії
- •Лекція хii тема: постійний струм план
- •Можна показати, що
- •Лекція хш тема: електричне поле в діелектриках план
- •Лекція х IV тема: магнітне поле план
- •Правило свердлика
- •Лекція XV
- •Тема: електромагнітна індукція.
- •Рівняння максвелла
- •Лекція XVI оптика тема: фотометрія. Інтерференція світла
- •Лекція XVII тема: дифракція
- •Лекція XVIII тема: електромагнітні хвилі в речовині
- •Лекція XIX квантова фізика тема: теплове випромінювання
- •Лекція хх тема: квантова природа світла
- •Лекція ххi тема: будова атома. Теорія бора
- •Лекція ххii тема: елементи квантової механіки
- •Лекція ххiii
- •Лекція ххiv тема: атомне ядро
Лекція х IV тема: магнітне поле план
1. Магнітне поле. Сила Ампера.
2. Сила Лоренца.
3. Закон БіоСавараЛапласа. Принцип суперпозиції. Приклади розрахунків полів.
4. Рамка зі струмом у магнітному полі.
5. Закон повного струму.
6. Магнітний потік. Теорема Гауса.
7. Робота з переміщення провідника зі струмом у магнітному полі.
1.
За відсутності струму провідники не взаємодіють. При пропусканні струму в однаковому напрямку вони будуть притягуватися. Тобто ми спостерігаємо факт взаємодії провідників унаслідок протікання через них струму. Оскільки цю взаємодію ми спостерігаємо об’єктивно, то повинно існувати таке матеріальне середовище, яке буде передавати цю взаємодію. Це матеріальне середовище має назву магнітне поле.
Магнітне поле це матеріальне середовище, яке оточує провідник зі струмом та рухомі електричні заряди.
Головна
характеристика магнітного поля
вектор магнітної індукції
![]() .
.
Його напрямок збігається з силою, яка діє на відповідний полюс магнітної стрілки, що поміщена в цю точку поля.
Опис
магнітного поля за допомогою вектора
![]()
це аналітичний підхід.
це аналітичний підхід.
Окрім цього, існує графічний засіб описання за допомогою силових ліній.
Силова
лінія
це така уявна лінія, у кожній точці якої
![]() збігається з вектором дотичної.
збігається з вектором дотичної.
Правило свердлика
Якщо поступальний рух свердлика вказує на напрямок струму, то обертальний рух його рукоятки вказує на напрямок силових ліній.
Числове значення сили, діючої на провідник зі струмом у магнітному полі, встановив Ампер, який показав, що для однорідного магнітного поля чисельне значення цієї сили визначається за формулою
d![]() =
I d
=
I d![]()
![]()
sin
( 1 )
sin
( 1 )
= ( B ,dl )
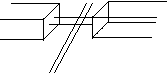 dl
dl
d![]() = I d
= I d![]()
![]()
( 1a )
( 1a )
|
B
dl |
sin = 1;
dl B ;
B
=
|
Вектор магнітної індукції чисельно дорівнює максимальній силі, яка діє на провідник одиничної довжини зі струмом, рівним одному амперу.
B = Tл ( тесла ); Tл = Н /( А м)
2.
Магнітне поле повинне діяти не тільки на провідник зі струмом, але й на рухомий заряд.
d![]() =
I
d
=
I
d![]()
![]()
j
= q n
![]() ;
;
J = q v n S; n = N / V;
Idl = q v n Sdl = q v dV ; Sdl = dV; n Sdl = dN;
dF = q dN
![]()
![]()
, dF / dN = Fл
, dF / dN = Fл
![]() л
це сила, яка діє на будь-яку заряджену
частинку, що, знаходячись в магнітному
полі, рухається зі швидкістю v.
л
це сила, яка діє на будь-яку заряджену
частинку, що, знаходячись в магнітному
полі, рухається зі швидкістю v.
![]() л
= q
л
= q
![]()
![]()
( 3 )
( 3 )
Із
формули (3) випливає, що
![]() л
завжди перпендикулярна швидкості
заряд-женої частинки.
л
завжди перпендикулярна швидкості
заряд-женої частинки.
![]() л
v
, тому
вона надає частинці доцентрового
прискорення, крім того, ця сила не виконує
роботи (
= 90,
cos
= 0).
л
v
, тому
вона надає частинці доцентрового
прискорення, крім того, ця сила не виконує
роботи (
= 90,
cos
= 0).
У загальному випадкові:
![]() л
=
q
л
=
q![]() + q
+ q
![]()
![]()
( 4 )
( 4 )
3. Закон Біо Савара Лапласа
Досліди показали, що:
1) Індукція магнітного поля прямо пропорційна силі струму в провідникові В ~ І.
2) В залежить від форми та розмірів провідника зі струмом у магнітному полі.
B = f ( форма і розміри )
3) У даній точці магнітного поля що залежить від розміщення цієї точці відносно провідника зі струмом.
Ці три
основні наслідки стимулювали появу
загального закону, який би дав можливість
обчислювати
![]() у будь-який точці магнітного поля.
у будь-який точці магнітного поля.
d![]() = к ( І / r3
)
d
= к ( І / r3
)
d![]()
![]() ,
( 5 )
,
( 5 )
де
d![]()
вектор, який чисельно дорівнює елементарній
довжині провідника зі струмом і збігається
з напрямком струму.
вектор, який чисельно дорівнює елементарній
довжині провідника зі струмом і збігається
з напрямком струму.
![]() радіус
- вектор, проведений від елемента
провідника d
радіус
- вектор, проведений від елемента
провідника d![]() в
розглядану точку поля.
в
розглядану точку поля.
к коефіцієнт пропорційності, який визначається дослідним шляхом.
dB
елементарна індукція. Вона перпендикулярна
площині, в якій лежать вектори d![]() і
і
![]() .
.
Для однорідного та ізотропного середовища:
|
к = кi CI : кi = 0 / 4 |
магнітна проникність; 0 магнітна стала
|
0 = 4 10-7 Гн / м
= 1 ( для вакууму )
dB = ( 0І / 4r2 ) dl sin ( 5a)
Закон БіоСавараЛапласа дає можливість знайти вектор магнітної індукції для струму, який тече в провідникові кінцевих розмірів, завдяки принципу суперпозиції
n
![]() =
=
![]() i
( 6 )
i
( 6 )
i = 1
де n - загальне число ділянок, на які розбито провідник.
Якщо
n
;
![]()
![]() =
=
![]()
![]() d
d![]() i
( 6а )
i
( 6а )
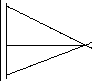
а) Для відрізка провідника:
B = 0І / 4r0 ( cos1 - cos2 )
б) Для нескінченно довгого провідника
1 0 ; 2
cos 1 - cos 2 = 2
B = 0І / 2r0.
в) B = 0І / 2R – у центрі колового провідника
г) У середині соленоїда
d
<<
![]()
l
B
= 0І
, n = N /
![]()
де n число витків.
a
|
4. a B
l І
n
F b
F h n |
Якщо струм у рамці відсутній, то результуюча сила, яка діє на рамку, дорівнює нулю. Якщо через рамку пропускати струм, то на горизонтальні ділянки рамки сила не діє, а на вертикальні ділянки діє момент пари сил, який дорівнює:
M
= 2F
h /2 = B І a
= B І S sin: |
Магнітний момент контуру зі струмом:
![]()
![]() m
= J S
m
= J S
![]() ,
,![]() = 1 ( 7 )
= 1 ( 7 )
M = рm B sin;
![]() =
=
![]() m
m
![]() ;
( 8 )
;
( 8 )
B



0 рm
5. Закон повного струму.
Як нам відомо, циркуляція вектора напруженості електричного поля по замкненому контуру дорівнює нулю. Це говорить про те, що електричне поле є потенційним.
![]() =
0.
=
0.
Для магнітного поля виділяємо контур
 І2
І2
І1
![]() (
9 )
(
9 )
Циркуляція
вектора
![]() вздовж замкненого контуру
вздовж замкненого контуру
![]() дорівнює
добутку магніт-ної сталої 0
на
алгебраїчну суму всіх струмів, які
охоплені цим контуром. Це твердження є
законом повного струму.
дорівнює
добутку магніт-ної сталої 0
на
алгебраїчну суму всіх струмів, які
охоплені цим контуром. Це твердження є
законом повного струму.
6.
Магнітний
потік через поверхню площиною dS
дорівнює добутку модуля вектора
![]() на елемент площини dS
та на cos.
на елемент площини dS
та на cos.
dФm = B dS cos; B
dФm = B dS;
n
= ( n ,B )
= 0о
(![]()
d
d![]() )
= dФm
( 10 )
)
= dФm
( 10 )
В електродинаміці доводиться теорема Остроградського Гауса: магнітний потік через будь-яку замкнену поверхню дорівнює нулю.
![]()
![]() d
d![]() = 0 ( 11 )
= 0 ( 11 )
Фізичний зміст формули: у природі не існують магнітні заряди, тому силові лінії магнітного поля завжди замкнені і магнітне поле не потенціальне, а вихрове, (на противагу електростатичному полю).
7.
Оскільки на провідник зі струмом у магнітному полі буде діяти Fамп , то він буде переміщуватись, а ця сила діє з боку магнітного поля, виконує роботу з переміщення провідника зі струмом у магнітному полі.
|
l F
|
dA = F dx = І Bl dx = І B dS = І dФm A = І Фm = І ( Ф2 - Ф1) A = ІФm ( 12 ) |

 dF
dF