
- •Кафедра фізики в.В.Соловйов, л.П.Давиденко Конспект лекцій із фізики
- •Полтава 2004
- •Тема: елементи кінематики
- •Лекція іі тема: динаміка частинок план
- •Лекція ііі тема: закони збереження. Тверде тіло план
- •Повний імпульс ізольованої (замкненої) механічної системи не змінюється при будь-яких взаємодіях у ній.
- •Трохи про консервативні системи
- •Швидкість зміни момента імпульсу відносно нерухомої точки о дорівнює результуючому моменту сил усіх зовнішніх сил.
- •Лекція IV тема: механічні коливання
- •Лекція V тема: механічні хвилі
- •Лекція vі тема : елементи механiки суцiльних середовищ
- •Лекція VII тема: макроскопічний стан
- •Лекція viiі тема: статистичний розподіл. Явища переносу
- •Лекція IX тема: основи термодинаміки
- •Лекція X тема: тверді тіла та рідини
- •Лекція XI тема: електростатика план
- •Механізм взаємодії
- •Лекція хii тема: постійний струм план
- •Можна показати, що
- •Лекція хш тема: електричне поле в діелектриках план
- •Лекція х IV тема: магнітне поле план
- •Правило свердлика
- •Лекція XV
- •Тема: електромагнітна індукція.
- •Рівняння максвелла
- •Лекція XVI оптика тема: фотометрія. Інтерференція світла
- •Лекція XVII тема: дифракція
- •Лекція XVIII тема: електромагнітні хвилі в речовині
- •Лекція XIX квантова фізика тема: теплове випромінювання
- •Лекція хх тема: квантова природа світла
- •Лекція ххi тема: будова атома. Теорія бора
- •Лекція ххii тема: елементи квантової механіки
- •Лекція ххiii
- •Лекція ххiv тема: атомне ядро
Лекція IV тема: механічні коливання
ПЛАН
1. Поняття про коливальний процес.
2. Кiнематика гармонiчних коливань.
3. Гармонiчний осцилятор. Маятники, вантаж на пружинi.
4. Енергетичне спiввiдношення для осцилятора.
5. Додавання коливань.
6. Вiльнi затухаючі коливання.
7. Вимушенi коливання осцилятора пiд дiєю синусоїдальної сили. Резонанс.
1. Пiд коливаннями в самому загальному випадкові розумiють рухи або процеси, якi мають певну повторюванiсть із часом.
Найбiльше значення у фiзицi мають механiчнi та електромагнiтні коливання.
Власнi, або вiльнi, коливання це такi коливання, якi виникають у системi, на яку не дiють зовнiшнi змiннi сили, а система приходить у коливання внаслiдок початкового вiдхилення вiд положення рiвноваги.
А якщо цi коливання виникають у консервативнiй системi, то вони будуть незатухаючими.
Коливальний рух є перiодичним, якщо значення фiзичної величини повторюється через певний промiжок часу.
Коливання рiзної фiзичної природи мають однаковi закономiрностi i тому описуються єдиним математичним апаратом.
2. Найбільш простий тип механiчних коливань гармонiчнi коливання. Це такi коливання, якi вiдбуваються за законом sin або cos.
Математично це можна представити так:
![]() (1)
(1)

 Х
Х


 t
t
Х змiщення точки вiд положення рiвноваги у момент часу t;
A амплiтуда коливань;
![]() фаза
коливань у момент часу t;
фаза
коливань у момент часу t;
![]() початкова
фаза;
початкова
фаза;
![]() циклiчна
(кругова)
частота;
циклiчна
(кругова)
частота;
![]() частота
коливань
кiлькiсть коливань за одиницю
частота
коливань
кiлькiсть коливань за одиницю
часу.
![]()
![]()
Амплiтуда величина максимального змiщення коливальної величини вiд положення рiвноваги.
Початкова фаза значення фази у момент часу t = 0.
![]()
T перiод коливань час одного повного коливання.
[T] = c.
3. Розглянемо коливання пружинного маятника.
Пружинний
маятник
це тiло масою m,
з`єднане з нерухомою пружиною з
коефiцiєнтом пружностi k,
що коливається в горизонтальній площинi
пiд дiєю сили
![]() ;
;









 mnp.
m
mnp.
m







![]()
![]()

Опишемо математично цей рух :
![]()
![]() (2)
(2)
- диференцiйне рiвняння гармонiчних коливань.
Нехай
![]() .Перевiримо,
чи задовольняе рiвняння (2) такому вигляду
х.
.Перевiримо,
чи задовольняе рiвняння (2) такому вигляду
х.
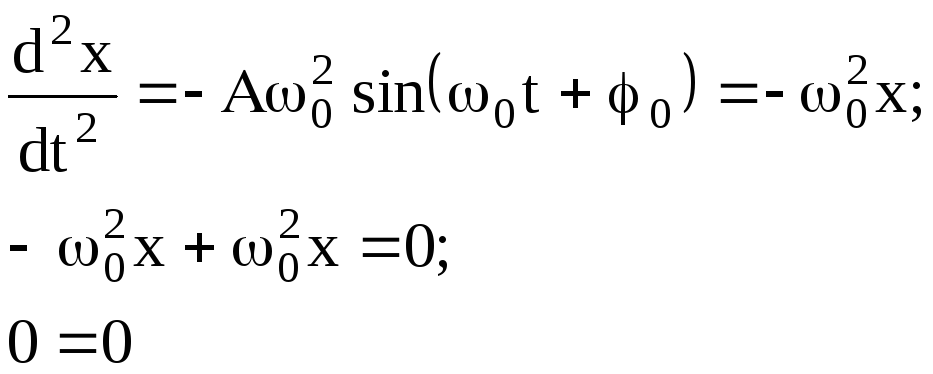
Наслiдки перевiрки:
1) рiвняння (1) є рiшенням диференцiйного рiвняння (2);
2)
коливання пружинного маятника є
гармонiчним
коливанням
із частотою
![]() .
.
3).
![]()
(сила пропорцiйна першому степеневі змiщення).
4).
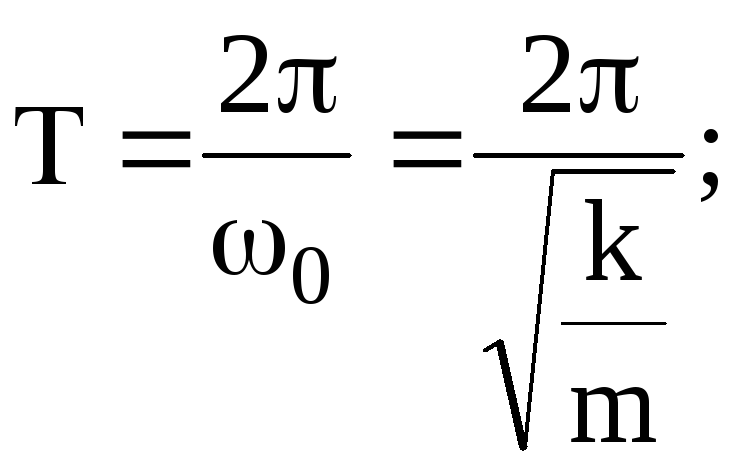
![]() (3)
(3)
Математичний маятник iдеалiзована система, яка складається iз матерiальної точки, що пiдвiшена на невагомій нерозтягнутій нитцi та здійснює малі коливання пiд дiєю сили тяжiння у вертикальній площині.



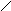
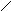






![]()




![]()






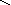


 Fтяж.
Fтяж.
![]()
Диференцiйне рiвняння руху має вигляд :
![]()
![]() (5),
тоді:
(5),
тоді:
![]() (4)
(4)
- диференцiйне рiвняння коливань математичного маятника.
Висновки:
1. F~X;
2. Коливання математичного маятнику теж є гармонiчнi.
3. З урахуванням (5) маємо :
![]() (6)
(6)
- перiод коливань математичного маятника.
Сили, якi за своєю дiєю аналогiчнi силам пружностi, називаються квазiпружними (квазi - майже), а звiдси випливає найбiльш загальне визначення гармонiчних коливань :
Гармонiчнi коливання це коливання, якi виникають пiд дiєю пружних або квазiпружних сил.
Фiзичний маятник це абсолютно тверде тiло, яке коливається вiдносно горизонтальної осi, яка не проходить через центр iнерцiї цього тiла.




 О
О






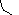


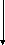


 C
C

![]()
 mg
mg
О'
Розглянемо
малi коливання фiзичного маятника
![]() :
:
Якщо вивести маятник iз положення рiвноваги, виникне обертальний момент, який буде прагнути повернути маятник у положення рiвноваги.
Можна показати, що диференцiйне рiвняння в цьому випадкові таке:
![]() (7)
(7)
l вiдстань мiж центром iнерцiї та вiccю обертання;
І момент iнерцiї маятника вiдносно вiсi обертання;
m маса маятника;
![]()
![]() (8)
(8)
- перiод коливань фiзичного маятника
![]() (9)
(9)
- приведена довжина фiзичного маятника
![]() (10)
(10)
Із
порiвняння формули (10) i (6) випливає, що
![]()
це довжина такого математичного маятника,
який коливається синхронно з фiзичним.
це довжина такого математичного маятника,
який коливається синхронно з фiзичним.
Усi вищенаведенi приклади являють собою частковi випадки коливань гармонiчного осцилятора.
Гармонiчний осцилятор це фiзична система, коливання якої можна представити таким диференцiйним рiвнянням:
![]() (11)
(11)
S коливальна величина.
Цi коливання становлять собою приклад гармонічного руху i тому можуть бути моделлю у багатьох галузях фiзики.
4.
![]()
![]() кiнетична
енергія тіла,
що
кiнетична
енергія тіла,
що
коливається.
Потенцiйна енергія тiла, що коливається, вимірюється роботою, яку виконує повертальна сила F = -kx, котра приводить тiло у положення рiвноваги
(En = A);
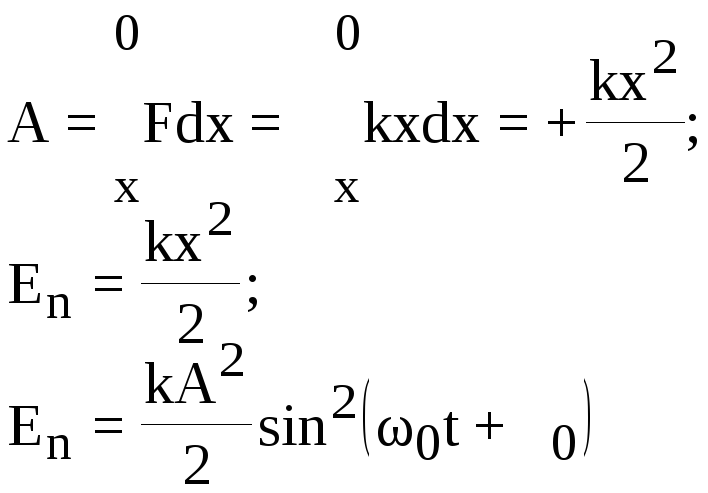
Вiдомо, що повна енергія коливань тiла = Ек + Еn




![]()
1
![]() (12)
(12)
повна механічна енергія тiла, що коливається.
5.
Кожне гармонiчне коливання можна
зобразити за допомогою векторної
дiаграми, якщо ввести обертальний вектор
амплітуди
![]() .
.
У
будь-який промiжок часу проекцiя кiнця
вектора
![]() буде змiнюватись так:
буде змiнюватись так:
![]()



![]()


![]()

 О
Х
О
Х
A
модуль вектора
![]() ;
;
![]() кутова
швидкiсть обертання вектора
кутова
швидкiсть обертання вектора
![]() навколо точки О (фiзичний змiст циклiчної
частоти
навколо точки О (фiзичний змiст циклiчної
частоти![]() );
);
![]() початкова
фаза.
початкова
фаза.
Використавши цей прийом, складемо 2 коливання однакової частоти та однакового напрямку :
![]()
![]()
Нехай результуюче коливання має такий вигляд :
![]()
Складемо вектори за правилом паралелограма:








 А
А




![]()


![]()







![]()
![]() С
С







![]()
![]() В
В
За допомогою теореми косинусів маємо:
![]() (13)
(13)
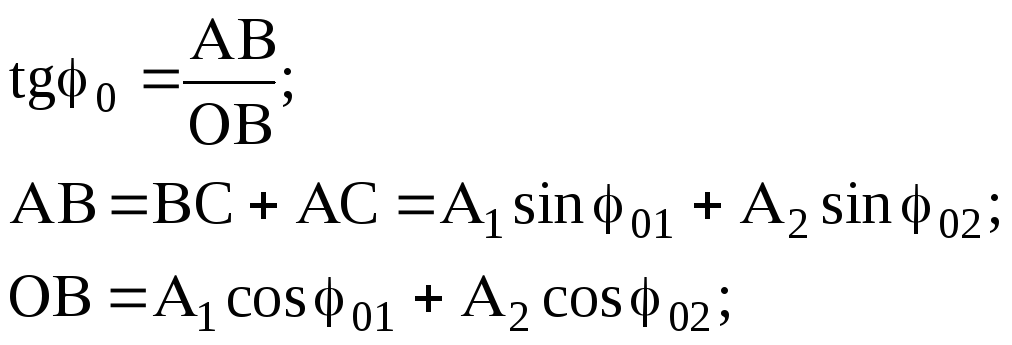
![]() (14)
(14)
Цей прийом є унiверсальним, оскільки вiн дозволяє скласти не тiльки 2 коливання, а й бiльше.
При складаннi 2-х взаємно перпендикулярних коливань у загальному випадку маємо складне рiвняння елiпсу.
Розглянемо частковий випадок, коли рiзниця фаз дорiвнюе 900:
![]()
![]()
![]()
![]()
![]()
![]()
![]()


 У
У


![]() Х
Х
6. Ранiше ми показали, що в консервативнiй cистемi пiд дiєю квазiпружних сил виникають вiльнi незатухаючі коливання, а якщо система буде дисипативною, то буде вiдбуватись відтiк енергії на виконання роботи проти сил тертя i внаслiдок цього коливання будуть затухати.
Уведемо
силу опору:
![]()
(на одній горизонталі).
![]()
![]() (15)
(15)
- диференцiйне рiвняння вiльних затухаючих коливань.
Можна показати, що рiшення цього диференцiйного рiвняння має такий вигляд :
![]() (16)
(16)

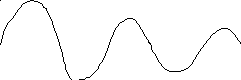



 t
t
At At+T
Таким чином, маємо затухаюче коливання, амплiтуда якого зменьшується з часом за таким законом :
![]()
Частота
![]()
Період
![]()
Уведемо
логарифмiчний декремент
![]() :
:
![]() це
величина, що дорiвнює натуральному
логарифму вiдношення двох послiдовних
амплiтуд, у моменти часу, що вiдрiзняється
на перiод коливань.
це
величина, що дорiвнює натуральному
логарифму вiдношення двох послiдовних
амплiтуд, у моменти часу, що вiдрiзняється
на перiод коливань.
![]() (17)
(17)
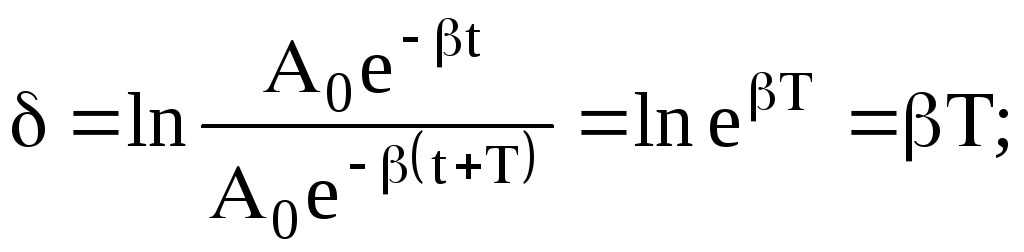
![]() (18)
(18)
![]() коефіцієнт
затухання.
коефіцієнт
затухання.
Розглянемо
фiзичний змiст
![]() i
i![]() .
.
Нехай
за час
![]() амплiтуда коливань зменшилась в е раз.
амплiтуда коливань зменшилась в е раз.
![]()
![]() (19)
(19)
Коефiцiєнт затухання обернений часу, за який амплiтуда коливань зменшилась в е раз.
Нехай
за час
![]() у
системi вiдбудеться N коливань.
у
системi вiдбудеться N коливань.
![]()
![]() (20)
(20)
Логарифмiчний декремент обернений кiлькостi коливань, по завершенні яких амплiтуда коливань зменшується в е раз.
7. А як одержати незатухаючi коливання в дисипативнiй системi?
Для цього потрiбна дiя зовнiшньої перiодичної сили, яка б протидiяла дисипацiї енергiї у системi.
Нехай ця сила має такий вигляд:
![]() зовнiшня
перiодична сила.
зовнiшня
перiодична сила.
Ця сила в певнi промiжки часу буде привносити енергiю в коливальну систему, внаслiдок чого коливання не будуть затухати.
Диференцiйне рiвняння буде мати такий вид:
![]()
![]() (21)
(21)
Можна показати, що у сталому режимi рiшення рiвняння має такий вигляд (за виглядом правої частини):
![]() (22)
(22)
Видно, що коливання будуть вiдбуватися з частотою зовнiшньої перiодичної сили F.
Можна показати, що
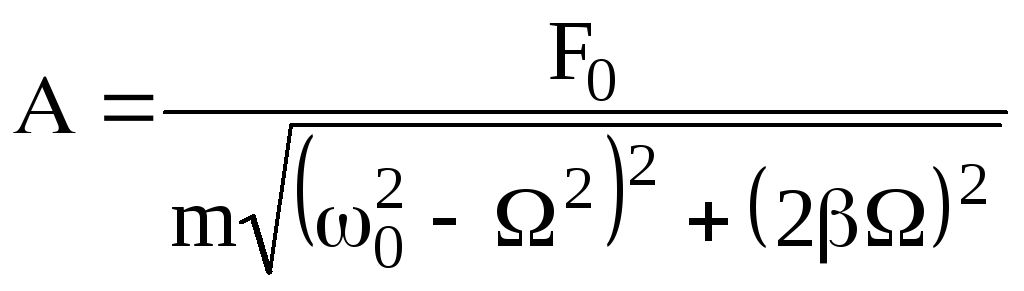 (23)
(23)
![]() (24)
(24)
Тобто
коливальний
рух визначається тiльки параметрами
самої коливальної системи
![]() .
.
Нехай
коефiцiєнт затухання
![]() .
Тодi, як видно iз (23),
.
Тодi, як видно iз (23),![]() .
.
![]() резонанс
резонанс
Резонанс
це явище рiзкого зростання амплiтуди
коливань при спрямуванні частоти
вимушеної сили
![]() до частоти власних коливань
до частоти власних коливань



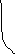
 A
A




А

 0
0









![]()
![]()
![]()
