Гіперболічний параболоїд
Досліджуємо поверхню, визначувану рівнянням
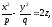(12.34)
де
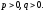Розітнемо
поверхню (12.34) площинами
.
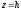Отримаємо
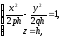
яка
при всіх значеннях
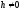є, гіперболою. При
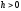її
дійсні осі паралельні осі
;
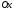при
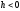— паралельні осі
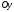; при
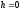лінія перетину 
розпадається на пару пересічних прямих
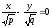і
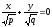. При перетині поверхні площинами,
паралельними площині
,
виходитимуть параболи
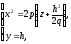
гілки
яких направлені вгору. При
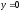в перетині виходить парабола
Рис.
95.
з
вершиною на початку координат і віссю
симетрії
.
Перетинаючи
поверхню (12.34) площинам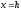и
,
отримаємо параболи
гілки яких направлені вниз.
Аналіз лінії перетину дозволяє визначити вид поверхні: вона має вид сідла (див. рис. 95). Поверхня (12.34) називається гіперболічним параболоїдом.
Конус другого порядку
Досліджуємо рівняння поверхні
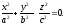(12.35)
Перетнемо
поверхню (12.35) площинами
.
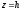Лінія перетину
.
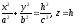При
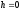вона вироджується в точку (0;0;0). При
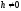в перетині одержуватимемо еліпси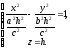
Напівосі
цих еліпсів зростатимуть при зростанні
.
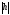Розітнемо
поверхню (12.35) площиною
.
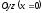Вийде лінія
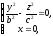
що розпадається на дві пересічні прямі
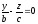і
.
При
перетині поверхні (12.35) площиною
у
=
0 отримаємо лінію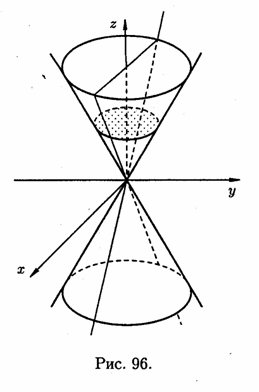
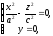
також що розпадається на дві пересічні прямі
і
Поверхня, визначувана рівнянням (12.35), називається конусом другого порядку, має вигляд, зображений на малюнку 96.
Поверхні, складені з прямих ліній, називаються лінійчатими. Такими поверхнями є циліндричні, конічні поверхні, а також однопорожнинний гіперболоїд і гіперболічний параболоїд.