
- •Рівняння площини в просторі
- •Загальне рівняння площини
- •Відстань від точки до площини
- •Рівняння прямої в просторі
- •2) Перетворення в нуль одного із знаменників рівнянь (12.13) означає перетворення в куль відповідного чисельника.
- •Умова, при якій дві прямі лежать в одній площині
- •Циліндричні поверхні
- •Нехай в площині лежить деяка лінія, рівняння якої (12.21)
- •Перетини твірної з еліпсом будуть. Виключимо, і з цих рівнянь і рівняння
- •4.1.9 Канонічні рівняння поверхонь другого порядку
- •Однопорожнинний гіперболоїд
- •Гіперболічний параболоїд
- •Конус другого порядку
Відстань від точки до площини
Нехай
задана точка
 і площина
і площина
 своїм рівнянням
своїм рівнянням
 . Відстань
. Відстань
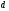 від точки
від точки
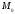 до площини
до площини
 знаходиться по формулі
знаходиться по формулі

Висновок
цієї формули такий же, як висновок
формули відстані від точки
 до прямої
до прямої
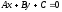 (див. с.61).
(див. с.61).
Відстань
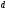 від точки
від точки
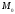 до площини
до площини
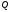 дорівнює модулю проекції вектора
дорівнює модулю проекції вектора ,
де
,
де
 — довільна точка площини
— довільна точка площини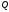 ,
на напрям нормального вектора
,
на напрям нормального вектора
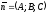 (див. рис. 74). Отже
(див. рис. 74). Отже

А
оскільки точка
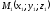 належить площині
належить площині ,
то
,
то
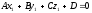 ,
тобто
,
тобто
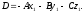
Тому
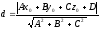 .
Відзначте, що якщо площина
.
Відзначте, що якщо площина
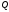 задана рівнянням
задана рівнянням
 то відстань від точки
то відстань від точки
 до площини
до площини
 може бути знайдено по формулі
може бути знайдено по формулі
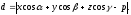
Рівняння прямої в просторі
Положення
прямої в просторі цілком визначено,
якщо задати яку
або крапку
 на прямій і вектор
на прямій і вектор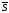 ,
паралельний цій прямій. Вектор
,
паралельний цій прямій. Вектор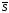 називається направляючим вектором
прямої. Нехай пряма
називається направляючим вектором
прямої. Нехай пряма
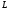 задана точкою
задана точкою
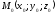 і направляючим вектором
і направляючим вектором
 . Візьмемо на прямій
. Візьмемо на прямій
 довільну точку
довільну точку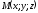 .
Позначимо
радіус-вектори точок
.
Позначимо
радіус-вектори точок
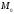 і
і
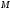 відповідно через
відповідно через
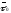 і
і
 .
Очевидно, що три вектори
.
Очевидно, що три вектори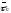 ,
,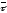 і
і
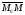 зв'язані співвідношенням
зв'язані співвідношенням
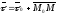 (12.10)
(12.10)
Вектор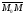 ,
що
лежить на прямій
,
що
лежить на прямій ,
паралельний
направляючому вектору
,
паралельний
направляючому вектору ,
тому
,
тому ,
де
,
де - скалярний множник, званий параметром,
може
приймати різні значення залежно від
положення
точки
- скалярний множник, званий параметром,
може
приймати різні значення залежно від
положення
точки
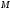 на прямій (див. рис. 75). Рівняння (12.10)
можна записати у вигляді
на прямій (див. рис. 75). Рівняння (12.10)
можна записати у вигляді
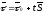 (12.11)
(12.11)
Отримане рівняння називається векторним рівнянням прямої.
Параметричні рівняння прямої
Помічаючи,
що,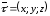 ,
,

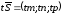 ,
рівняння
(12.11) можна записати у вигляді
,
рівняння
(12.11) можна записати у вигляді
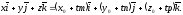
Звідси
слідує рівність:
 (12.12)
(12.12)
Вони називаються параметричними рівняннями прямої в просторі. Канонічні рівняння прямої
Нехай
 — направляючий вектор прямої
— направляючий вектор прямої
 і
і
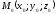 — точка, що лежить на цій прямій. Вектор
— точка, що лежить на цій прямій. Вектор ,
що сполучає точку
,
що сполучає точку
 з довільною точкою
з довільною точкою
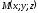 прямої
прямої ,
паралель вектору
,
паралель вектору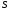 . Тому координати вектора
. Тому координати вектора
 і вектора
і вектора
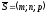 пропорційні:
пропорційні:
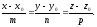 (12.13)
(12.13)
Рівняння (12.13) називаються канонічним рівняннями прямої в просторі.
Зауваження: 1) Рівняння (12.13) можна було б отримати відразу з параметричних рівнянь прямої (12.12), виключивши параметр t. З рівнянь (12.12) знаходимо

2) Перетворення в нуль одного із знаменників рівнянь (12.13) означає перетворення в куль відповідного чисельника.
Наприклад,
рівняння
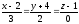 задають пряму, що проходить через
точку
задають пряму, що проходить через
точку
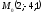 перпендикулярно осі
перпендикулярно осі
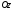 (проекція
вектора
(проекція
вектора
 на
вісь
на
вісь
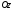 рівна
нулю). Але це означає, що пряма лежить
в площині
рівна
нулю). Але це означає, що пряма лежить
в площині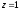 ,
і
тому для всіх точок прямої буде
,
і
тому для всіх точок прямої буде
 .
.
Рівняння
прямої в просторі, що проходить через
дві точки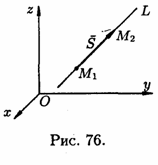
Нехай
пряма
 проходить через точки
проходить через точки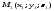 ,
і
,
і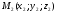 . Як направляючий вектор
. Як направляючий вектор
 можна узяти вектор
можна узяти вектор ,
тобто
,
тобто
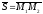 (див. рис. 76). Отже
(див. рис. 76). Отже
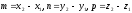 .
Оскільки пряма проходить через точку
.
Оскільки пряма проходить через точку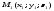 ,
то, згідно рівнянням (12.13), рівняння
прямої
,
то, згідно рівнянням (12.13), рівняння
прямої
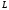 мають вигляд
мають вигляд
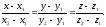 (12.14)
(12.14)
Рівняння (12.14) називаються рівняннями прямої, що проходить через дві дані точки.
Загальні рівняння прямої
Пряму в просторі можна задати як лінію перетину двох непаралельних площин. Розглянемо систему рівнянь
 (12.15)
(12.15)
Кожне
з рівнянь цієї системи визначає площину.
Якщо,
площини не паралельні (координати
векторів
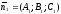 і
і
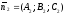 не пропорційні), то система (12.15) визначає
пряму
не пропорційні), то система (12.15) визначає
пряму
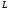 як геометричне місце точок простору,
координати яких задовольняють кожному
з рівнянь системи (див. рис. 77). Рівняння
(12.15) називають загальними рівняннями
прямої.
як геометричне місце точок простору,
координати яких задовольняють кожному
з рівнянь системи (див. рис. 77). Рівняння
(12.15) називають загальними рівняннями
прямої.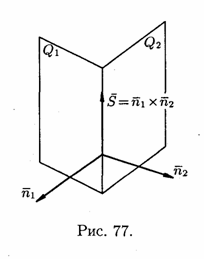
Від
загальних рівнянь (12.15) можна перейти
до канонічних рівнянь
(12.13). Координати точки на прямій
на прямій
 одержуємо
з системи рівнянь (12.15), додавши одну з
координат довільне значення (наприклад,
2 = 0). Оскільки пряма перпендикулярна
векторам
одержуємо
з системи рівнянь (12.15), додавши одну з
координат довільне значення (наприклад,
2 = 0). Оскільки пряма перпендикулярна
векторам
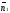 і
і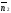 ,
то за направляючий вектор
,
то за направляючий вектор
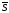 прямої
прямої
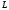 можна прийняти векторний добуток
можна прийняти векторний добуток
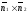 :
:
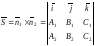
Зауваження: Канонічні рівняння прямої легко отримати, узявши дві які-небудь точки на ній і застосувавши рівняння (12.14).
Приклад
12.1.
Написати
канонічні рівняння прямої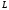 ,
заданою
рівнянням
,
заданою
рівнянням

Рішення:
Покладемо
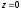 і вирішимо систему точку
і вирішимо систему точку
 .
Покладемо
.
Покладемо
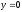 і вирішимо систему
і вирішимо систему
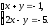
Знаходимо
другу точку
 прямої
прямої
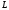 .
Записуємо рівняння прямої
.
Записуємо рівняння прямої ,
що проходить через точки
,
що проходить через точки
 і
і
 :
:
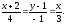
Пряма лінія в просторі. Основні задачі
Кут між прямими. Умови паралелі і перпендикулярності прямих
Нехай
прямі
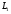 і
і
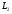 задані рівняннями
задані рівняннями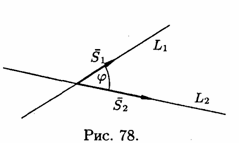

і

Під
кутом між цими прямими розуміють кут
між
направляючими векторами
 і
і
 (див. рис. 78). Тому, по відомій формулі
для косинуса кута між векторами,
одержуємо
(див. рис. 78). Тому, по відомій формулі
для косинуса кута між векторами,
одержуємо
 або
або
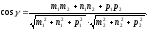 (12.16)
(12.16)
Для
знаходження гострого кута між прямими
 і
і
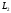 чисельник правої частини формули
(12.16) слідує узяти по модулю.
чисельник правої частини формули
(12.16) слідує узяти по модулю.
Якщо
прямі
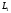 і
і
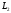 перпендикулярні, то в цьому і тільки в
цьому випадку маємо
перпендикулярні, то в цьому і тільки в
цьому випадку маємо
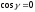 . Отже, чисельник дробу (12.16) рівний нулю,
тобто
. Отже, чисельник дробу (12.16) рівний нулю,
тобто
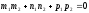 .
.
Якщо
прямі
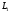 і
і
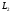 паралеьні, то паралеьні їх направляючі
вектори
паралеьні, то паралеьні їх направляючі
вектори
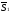 і
і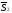 . Отже, координати цих векторів
пропорційні, тобто
. Отже, координати цих векторів
пропорційні, тобто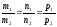 .
.
Приклад
12.2. Знайти кут між прямими
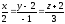 і
і
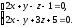
Розв’язок:
Очевидно,
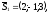 а
а ,
де
,
де
 .
Звідси витікає, що
.
Звідси витікає, що
 .
Оскільки
.
Оскільки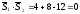 ,
то
,
то .
.
