
- •Рівняння площини в просторі
- •Загальне рівняння площини
- •Відстань від точки до площини
- •Рівняння прямої в просторі
- •2) Перетворення в нуль одного із знаменників рівнянь (12.13) означає перетворення в куль відповідного чисельника.
- •Умова, при якій дві прямі лежать в одній площині
- •Циліндричні поверхні
- •Нехай в площині лежить деяка лінія, рівняння якої (12.21)
- •Перетини твірної з еліпсом будуть. Виключимо, і з цих рівнянь і рівняння
- •4.1.9 Канонічні рівняння поверхонь другого порядку
- •Однопорожнинний гіперболоїд
- •Гіперболічний параболоїд
- •Конус другого порядку
Перетини твірної з еліпсом будуть. Виключимо, і з цих рівнянь і рівняння
(точка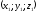 лежить
на еліпсі)
лежить
на еліпсі)
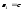 .
Маємо:
:
.
Маємо:
:
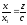 ,
,
 .
.
Звідси
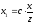 і
і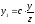 . Підставляючи значення
. Підставляючи значення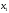 і
і
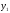 в рівняння еліпса (12.27), отримаємо
в рівняння еліпса (12.27), отримаємо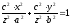 або
або

Це і є шукане рівняння конуса. •
4.1.9 Канонічні рівняння поверхонь другого порядку
По заданому рівнянню поверхні другого порядку (тобто поверхні, рівняння якої в прямокутній системі координат є рівнянням алгебри другого ступеня) визначатимемо її геометричний вид. Для цього застосовний так званий метод перетинів. дослідження вода поверхні проводитимемо за допомогою вивчення ліній перетину даної поверхні з координатними площинами або площинами, ним паралельними.
Еліпсоїд
Досліджуємо поверхню, задану рівнянням
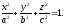 (12.28)
(12.28)
Розглянемо перетини поверхні (12.28) з площинами, паралельними
площини
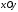 .
Рівняння таких площин:
.
Рівняння таких площин:
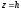 ,
де
,
де
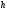 —
будь-яке число.
Лінія, одержувана в перетині, визначається
двома рівняннями
—
будь-яке число.
Лінія, одержувана в перетині, визначається
двома рівняннями
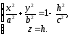 (12.29)
(12.29)
Досліджуємо рівняння (12.29):
а)
Якщо
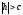 ,
,
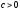 то
то
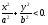 Точок
перетину поверхні
(12.28) з площинами
Точок
перетину поверхні
(12.28) з площинами
 не існує.
не існує.
б)
Якщо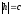 ,
,
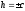 то
то
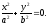 Лінія
перетину (12.29) вироджується
в дві точки
Лінія
перетину (12.29) вироджується
в дві точки
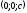 і
і
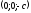 .
Площини
.
Площини
 і
і
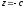 торкаються
даної поверхні.
торкаються
даної поверхні.
в)Якщо
 ,
то рівняння (12.29) можна переписати у
вигляді:
,
то рівняння (12.29) можна переписати у
вигляді: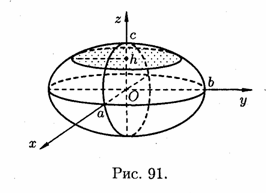
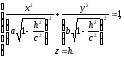
Як видно, лінія перетину є еліпс з напівосями (див. рис. 91)
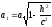 і
і

При
цьому чим менше ,
тим
більше напівосі
,
тим
більше напівосі
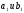 .
При
.
При вони досягають своїх найбільших
значень:
вони досягають своїх найбільших
значень:
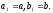 Рівняння
(12.29) приймуть вигляд
Рівняння
(12.29) приймуть вигляд
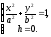
Аналогічні
результати отримаємо, якщо розглянемо
перетини поверхні (12.28)
площинами
 і
і

Таким
чином, розглянуті перетини дозволяють
зобразити поверхню
(12.28) як замкнуту овальну поверхню.
Поверхня (12.28) називається
еліпсоїдом.
Величини і
і
 називаються напівосями еліпсоїда.
Якщо всі вони різні, то еліпсоїд
називається трьовісним.
Якщо
які-небудь дві напівосі рівні, тривісний
еліпсоїд перетворюється на
еліпсоїд
обертання, якщо
називаються напівосями еліпсоїда.
Якщо всі вони різні, то еліпсоїд
називається трьовісним.
Якщо
які-небудь дві напівосі рівні, тривісний
еліпсоїд перетворюється на
еліпсоїд
обертання, якщо
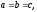 то — в сферу
то — в сферу

Однопорожнинний гіперболоїд
Досліджуємо поверхню, задану рівнянням
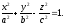 (12.30)
(12.30)
Перетинаючи
поверхню (12.30) площини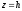 ,
отримаємо лінію перетину, рівняння
якої мають вигляд
,
отримаємо лінію перетину, рівняння
якої мають вигляд

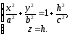 або
або
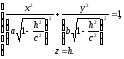
Як видно, цією лінією є еліпс з напівосями
 і
і
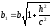
Напівосі
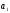 і
і
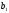 досягають свого якнайменшого значення
при:
досягають свого якнайменшого значення
при:
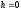 ,
,
 ,
,
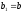 .
При
.
При
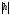 зростанні
напівосі еліпса збільшуватимуться.
зростанні
напівосі еліпса збільшуватимуться.
Якщо
перетинати поверхню (12.30) площинами
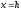 або
або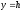 ,
то
в перетині отримаємо гіперболи. Знайдемо,
наприклад ,
лінію перетину поверхні (12.30) з
площиною
,
то
в перетині отримаємо гіперболи. Знайдемо,
наприклад ,
лінію перетину поверхні (12.30) з
площиною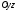 рівняння
якої
рівняння
якої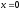 .
Ця лінія перетину описується
рівняннями
.
Ця лінія перетину описується
рівняннями
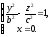
Як видно, ця лінія є гіпербола (див. рис. 92).Аналіз цих перетинів показує, що поверхня, визначувана рівнянням (12.30), має форму нескінченної трубки, що розширяється. Поверхня (12.30) називається однопорожнинним гіперболоїдом.
Зауваження: можна довести, що через будь-яку точку гіперболоїда (12.30) проходять дві прямі, лежачі на ньому.
Двопорожнинний гіперболоїд
Нехай поверхня задана рівнянням
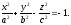 (12.31)
(12.31)
Якщо поверхню (12.31) перетнути площинами z = h, то лінія перетину визначається рівняннями
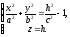 (12.32)
(12.32)
Звідси витікає, що:
а) Якщо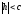 ,
то
площини
,
то
площини
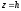 не перетинають поверхні;
не перетинають поверхні;
б) Якщо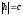 ,
то
площини
,
то
площини
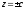 торкаються даної поверхні
відповідно
в точках
торкаються даної поверхні
відповідно
в точках
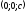 і
і
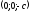 .
.
в) Якщо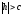 ,
то рівняння (12.32) можуть
бути переписаний
так
,
то рівняння (12.32) можуть
бути переписаний
так
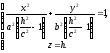
Ці
рівняння визначають еліпс, напівосі
якого зростають
із зростанням
 .
.
Рис. 93.
Перетинаючи
поверхню (12.31) координатними площинами
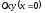 і
і
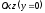 ,
отримаємо
в перетині гіперболи, рівняння яких
відповідно
мають вигляд
,
отримаємо
в перетині гіперболи, рівняння яких
відповідно
мають вигляд
 і
і

У
обох гіпербол дійсною віссю є вісь
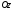 .
Метод перетину дозволяє зобразити
поверхню (див. рис. 93), визначувану
рівнянням (12.31), як поверхню, що складається
з двох порожнин, що мають форму опуклих
необмежених чаш. Поверхня (12.31) називається
двопорожнинним гіперболоїдом
.
Метод перетину дозволяє зобразити
поверхню (див. рис. 93), визначувану
рівнянням (12.31), як поверхню, що складається
з двох порожнин, що мають форму опуклих
необмежених чаш. Поверхня (12.31) називається
двопорожнинним гіперболоїдом
Еліптичний параболоїд
Досліджуємо
поверхню, задану рівнянням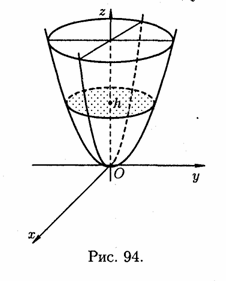
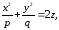 (12.33)
(12.33)
де
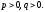 Розітнемо поверхню (12.33) площинами
Розітнемо поверхню (12.33) площинами
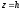 .
В перетині отримаємо лінію, рівняння
якою є
.
В перетині отримаємо лінію, рівняння
якою є

Якщо
 ,
то
площини
,
то
площини
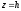 поверхні
не перетинають;
якщо
поверхні
не перетинають;
якщо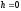 ,
то площина
,
то площина
 торкається поверхні в точці (0;0;0);
торкається поверхні в точці (0;0;0);

якщо ,
то в перетині маємо еліпс, рівняння
якого має вигляд
,
то в перетині маємо еліпс, рівняння
якого має вигляд
Його
напівосі зростають із зростанням.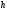 .
При
перетині поверхні (12.33) координатними
площинами Oxz
і
Oyz
вийдуть
відповідно параболи
.
При
перетині поверхні (12.33) координатними
площинами Oxz
і
Oyz
вийдуть
відповідно параболи
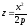 і
і
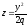 . Таким чином, поверхня, визначувана
рівнянням (12.33), має вид опуклої,
нескінченно розширяється чаші (див.
рис. 94). Поверхня (12.33) називається
еліптичним параболоїдом.
. Таким чином, поверхня, визначувана
рівнянням (12.33), має вид опуклої,
нескінченно розширяється чаші (див.
рис. 94). Поверхня (12.33) називається
еліптичним параболоїдом.
