
- •Рівняння площини в просторі
- •Загальне рівняння площини
- •Відстань від точки до площини
- •Рівняння прямої в просторі
- •2) Перетворення в нуль одного із знаменників рівнянь (12.13) означає перетворення в куль відповідного чисельника.
- •Умова, при якій дві прямі лежать в одній площині
- •Циліндричні поверхні
- •Нехай в площині лежить деяка лінія, рівняння якої (12.21)
- •Перетини твірної з еліпсом будуть. Виключимо, і з цих рівнянь і рівняння
- •4.1.9 Канонічні рівняння поверхонь другого порядку
- •Однопорожнинний гіперболоїд
- •Гіперболічний параболоїд
- •Конус другого порядку
Нехай в площині лежить деяка лінія, рівняння якої (12.21)
Теорема
12.1. Рівняння циліндра, твірні якого
паралельні осі Oz,
має
вигляд (12.21), тобто не містить координати
z.
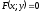 (12.21)
(12.21)
Побудуємо
циліндр із твірними паралельними осі
 і направляючою
і направляючою
 .
.
Візьмемо
на циліндрі будь-яку точку
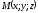 (див. рис. 84). Вона лежить на якійсь
твірній. Нехай
(див. рис. 84). Вона лежить на якійсь
твірній. Нехай
 — точка перетину цієї твірної з площиною
— точка перетину цієї твірної з площиною . Отже, точка
. Отже, точка
 лежить на кривій
лежить на кривій
 і її
координати
задовольняють рівнянню (12.21).
і її
координати
задовольняють рівнянню (12.21).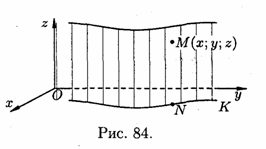
Але
точка
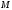 має такі ж абсцису
має такі ж абсцису
 и ординату
и ординату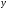 ,
що і точка
,
що і точка
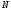 .
Отже, рівнянню (12.21) задовольняють і
координати точки
.
Отже, рівнянню (12.21) задовольняють і
координати точки ,
оскільки воно не містить
,
оскільки воно не містить
 .
І оскільки
.
І оскільки
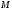 — це будь-яка точка циліндра, те рівняння
(12.21) і буде рівнянням цього циліндра.
— це будь-яка точка циліндра, те рівняння
(12.21) і буде рівнянням цього циліндра.
Тепер
ясно, що
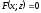 є рівняння циліндра із твірними,
паралельними осі
є рівняння циліндра із твірними,
паралельними осі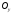 ,
а
,
а
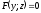 — з твірними, паралельними осі
— з твірними, паралельними осі
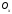 .
Назва циліндра визначається назвою
направляючої.
Якщо направляючій служить еліпс
.
Назва циліндра визначається назвою
направляючої.
Якщо направляючій служить еліпс
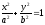
в
площині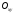 ,
то
відповідна циліндрова поверхня
називається еліптичним
циліндром (див.
рис. 85).
,
то
відповідна циліндрова поверхня
називається еліптичним
циліндром (див.
рис. 85).


Окремим
випадком еліптичного циліндра
є круговий
циліндр, його
рівняння
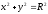 .
Рівняння
.
Рівняння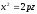 визначає в просторі параболічний
циліндр (див. рис. 86). Рівняння
визначає в просторі параболічний
циліндр (див. рис. 86). Рівняння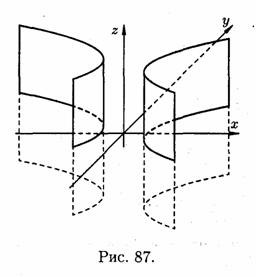
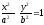
визначає в просторі гіперболічний циліндр (див. рис. 87).
Всі
ці поверхні називаються циліндрами
другого порядку, оскільки
їх
рівняння є рівняння другого ступеня
відносно поточних координат
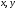 і
і
 .
.
Рис.
87.
Поверхня,
утворена обертанням деякої плоскої
кривої навкруги осі,
що лежить в її площині, називається
поверхнею
обертання. Нехай
деяка крива
 лежить в площині
лежить в площині
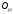 . Рівняння цієї кривої
. Рівняння цієї кривої
запишуться у вигляді
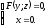 (12.22)
(12.22)
Знайдемо
рівняння поверхні, утвореної обертанням
кривої
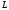 навкруги осі
навкруги осі .
.
Візьмемо
на полощині
довільну
точку
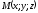 (см. рис. 88).
віссю
(см. рис. 88).
віссю
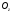 і
кривої
і
кривої
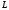 відповідно
через
відповідно
через
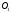 і
і
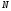 .
Позначимо
координати
точки
.
Позначимо
координати
точки
 через
через
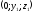 .
Відрізки
.
Відрізки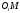 і
і
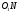 є
радіусами
одної
і
тієї ж округи
. Тому
є
радіусами
одної
і
тієї ж округи
. Тому .
Але
.
Але
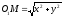
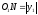 .
То,
.
То,
 або
або
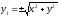 .
Окрім
цього,
очевидно
.
Окрім
цього,
очевидно
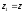 .
.
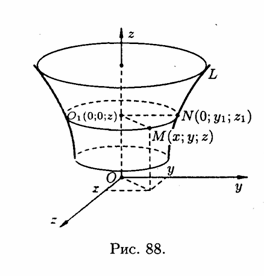
Оскільки
точка
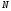 лежить на кривій
лежить на кривій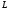 ,
то її координати задовольняють рівнянню
(12.22), Отже
,
то її координати задовольняють рівнянню
(12.22), Отже . Виключаючи допоміжні координати
. Виключаючи допоміжні координати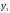 і
і
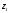 точки
точки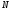 ,
приходимо до рівняння
,
приходимо до рівняння (12.23)
(12.23)
Рис.
88. цієї поверхні і не задовольняють
координати точок, що не лежать на
поверхні обертання.
цієї поверхні і не задовольняють
координати точок, що не лежать на
поверхні обертання.
Як
видно, рівняння (12.23) виходить з (12.22)
простої заміною
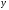 на
на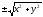 ,
координата я зберігається.
,
координата я зберігається.
Зрозуміло,
що якщо крива (12.22) обертається навкруги
ос і,
то рівняння поверхні обертання має
вигляд
і,
то рівняння поверхні обертання має
вигляд
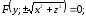
Рис.
89. і її рівняння
і її рівняння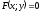 ,
то рівняння поверхні обертання, утвореної
обертанням кривої навкруги осі
,
то рівняння поверхні обертання, утвореної
обертанням кривої навкруги осі ,
є
,
є
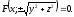
Так,
наприклад, обертаючи пряму
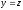 навкруги осі
навкруги осі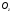 (див. рис. 89), отримаємо поверхню обертання
(її рівняння
(див. рис. 89), отримаємо поверхню обертання
(її рівняння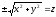 або
або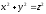 ).
Вона називається конусом другого
порядку.
).
Вона називається конусом другого
порядку.
Поверхня,
утворена прямими
лініями, що проходять через дану точку
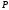 і
перетинаючими дану плоску лінію
і
перетинаючими дану плоску лінію
 (не проходить через
(не проходить через ),
називається конічною поверхнею конусом.
При цьому лінія
),
називається конічною поверхнею конусом.
При цьому лінія називається направляючою конуса,
точка
називається направляючою конуса,
точка — її вершиною, а пряма, описує поверхня,
називається утворюючою.
Нехай
направляюча
— її вершиною, а пряма, описує поверхня,
називається утворюючою.
Нехай
направляюча
 задана рівняннями
задана рівняннями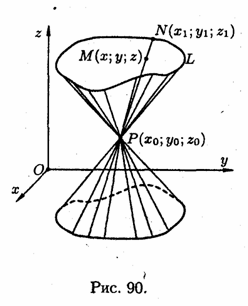
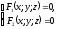 (12.24)
(12.24)
а
точка — вершина конуса. Знайдемо рівняння
конуса.
— вершина конуса. Знайдемо рівняння
конуса.
Візьмемо
на поверхні конуса довільну точку
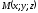 (див. рис. 90). Твірна, що проходить через
точки
(див. рис. 90). Твірна, що проходить через
точки
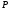 і
і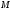 ,
перетне направляючу
,
перетне направляючу
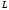 в деякій точці
в деякій точці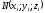 . Координати точки
. Координати точки
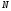 задовольняють рівнянням (12.24) направляючої.
задовольняють рівнянням (12.24) направляючої.
 (12.25)
(12.25)
Канонічні
рівняння твірних, що проходять через
точки
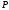 і
і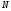 ,
мають вигляд
,
мають вигляд
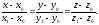 (12.26)
(12.26)
Виключаючи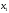 ,
,
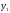 і
і
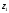 з рівнянь (12.25) і (12.26), отримаємо рівняння
конічної поверхні, що зв'язує поточні
координати
з рівнянь (12.25) і (12.26), отримаємо рівняння
конічної поверхні, що зв'язує поточні
координати
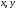 і
і
 .
.
.
.
Приклад
12.3.
Скласти
рівняння конуса з вершиною в точці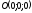 ,
якщо
направляючій служить еліпс
,
якщо
направляючій служить еліпс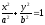 ,
що лежить в площині
,
що лежить в площині
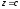 .
.
Розв’язок:
Нехай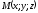 —
будь-яка точка конуса. Канонічні рівняння
твірних,
що проходять через точки
—
будь-яка точка конуса. Канонічні рівняння
твірних,
що проходять через точки
 і точку
і точку

