
- •Рівняння площини в просторі
- •Загальне рівняння площини
- •Відстань від точки до площини
- •Рівняння прямої в просторі
- •2) Перетворення в нуль одного із знаменників рівнянь (12.13) означає перетворення в куль відповідного чисельника.
- •Умова, при якій дві прямі лежать в одній площині
- •Циліндричні поверхні
- •Нехай в площині лежить деяка лінія, рівняння якої (12.21)
- •Перетини твірної з еліпсом будуть. Виключимо, і з цих рівнянь і рівняння
- •4.1.9 Канонічні рівняння поверхонь другого порядку
- •Однопорожнинний гіперболоїд
- •Гіперболічний параболоїд
- •Конус другого порядку
Основні поняття.
Рівняння площини в просторі.
Площина. Основні задачі.
Рівняння прямої в просторі.
Пряма лінія в просторі. Основні задачі.
Пряма і площина в просторі. Основні задачі.
Циліндричні поверхні.
Поверхні обертання. Конічні поверхні.
Канонічне Рівняння поверхні другого порядку.
Рівняння площини в просторі
Найпростішою
поверхнею є площина. Площину в просторі
 можна задати різними способами. Кожному
з них відповідає певний вид її рівняння.
можна задати різними способами. Кожному
з них відповідає певний вид її рівняння.
Рівняння площини, що проходить через дану точку перпендикулярно даному вектору
Нехай
у просторі
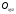 площина
площина
 задана
точкою
задана
точкою
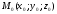 і вектором
і вектором
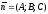 ,
перпендикулярним
цій площині(см. рис. 69). Виведемо
рівняння площини
,
перпендикулярним
цій площині(см. рис. 69). Виведемо
рівняння площини
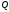 .
Візьмемо
на ній довільну точку
.
Візьмемо
на ній довільну точку
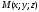 і
складемо вектор
і
складемо вектор
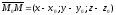 .
При
довільному місці точки
.
При
довільному місці точки
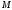 на
площині
на
площині
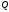 вектори
вектори
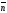 и
и
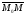 взаємно перпендикулярні, тому їх
скалярний добуток дорівнює нулю:
взаємно перпендикулярні, тому їх
скалярний добуток дорівнює нулю:
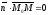 ,
тобто
,
тобто
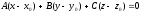 .
(12.3)
.
(12.3)
Координати
будь-якої точки
площини
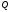 задовольняють рівняння (12.3), координати
точок, що не лежать на площині, цьому
рівнянню не задовольняють (для
задовольняють рівняння (12.3), координати
точок, що не лежать на площині, цьому
рівнянню не задовольняють (для
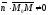 ).
).
Рівняння
(12.3)
називається рівнянням
площини, що проходить через
дану
точку
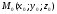 перпендикулярно вектору
перпендикулярно вектору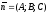 .
Воно першого ступеня відносно поточних
координат
.
Воно першого ступеня відносно поточних
координат
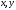 і
і
 .
Вектор
.
Вектор
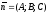 називається
нормальним вектором площини.
називається
нормальним вектором площини.
Додаючи
коефіцієнтам
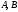 і
і
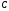 рівняння (12.3) різні значення, можна
отримати рівняння будь-якої площини,
що проходить вектор
рівняння (12.3) різні значення, можна
отримати рівняння будь-якої площини,
що проходить вектор
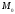 .
Сукупність площин, що проходять через
дану точку, називається зв'язкою площин,
а рівняння (12.3) — рівнянням зв'язку
площин.
.
Сукупність площин, що проходять через
дану точку, називається зв'язкою площин,
а рівняння (12.3) — рівнянням зв'язку
площин.
Загальне рівняння площини
Розглянемо
загальне рівняння першого ступеня з
трьома змінними
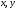 і
і
 :
:
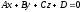 .
(12.4)
.
(12.4)
Вважаючи
що, принаймні, один з коефіцієнтів
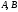 або
або
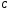 не рівний нулю, наприклад
не рівний нулю, наприклад
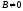 ,
перепишемо рівняння (12.4) у вигляді
,
перепишемо рівняння (12.4) у вигляді
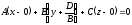 (12.5)
(12.5)
Порівнюючи
рівняння (12.5) з рівнянням (12.3), бачимо,
що рівняння
(12.4) і (12.5) є рівнянням площини з нормальним
вектором
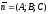 ,
що
проходить через точку
,
що
проходить через точку
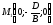 .
.
Отже,
рівняння (12.4) визначає в системі координат
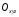 деяку
площину.
Рівняння (12.4) називається загальним
рівнянням площини.
деяку
площину.
Рівняння (12.4) називається загальним
рівнянням площини.
Окремі випадки загального рівняння площини:
-
Якщо
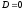 ,
то воно приймає, вигляд
,
то воно приймає, вигляд
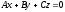 .
Цьому рівнянню задовольняє точка
.
Цьому рівнянню задовольняє точка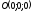 .Отже,
в цьому випадку площина проходить
через початок координат.
.Отже,
в цьому випадку площина проходить
через початок координат. -
Якщо
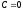 ,
то маємо рівняння
,
то маємо рівняння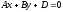 .
Нормальний вектор
.
Нормальний вектор
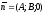 перпендикулярний осі Oz. Отже, площина
паралель осі Oz; якщо
перпендикулярний осі Oz. Отже, площина
паралель осі Oz; якщо
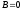 — паралель осі
— паралель осі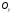 ,
,
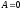 — паралель осі
— паралель осі
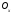 .
. -
Якщо
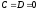 ,
то площина проходить через
,
то площина проходить через
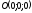 паралель осі
паралель осі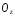 ,
тобто площина
,
тобто площина
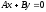 проходить через вісь
проходить через вісь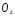 .
Аналогічно рівнянням
.
Аналогічно рівнянням
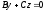 і
і
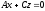 , відповідають площини, що проходять
відповідно через осі
, відповідають площини, що проходять
відповідно через осі
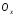 і
і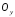 .
. -
Якщо
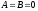 ,
то рівняння (12.4) приймає вигляд
,
то рівняння (12.4) приймає вигляд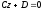 тобто
.
тобто
.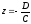 Площина
паралельна
площині.
Площина
паралельна
площині.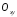 Аналогічно,
рівнянням
Аналогічно,
рівнянням
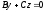 і відповідають
і відповідають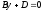 площини,
відповідно паралельні площинам
площини,
відповідно паралельні площинам
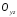 і
і
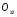 .
. -
Якщо
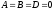 ,
то рівняння (12.4) прикмет вигляд
,
то рівняння (12.4) прикмет вигляд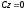 ,
тобто
,
тобто
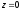 .
Це рівняння площини
.
Це рівняння площини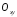 .
Аналогічно:
.
Аналогічно:
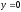 — зрівняний площині
— зрівняний площині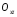 ;
;
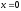 —
рівняння площини
—
рівняння площини
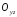 .
.
Рівняння площини, що проходить через три дані точки
Три
точки простору, не лежачі па однієї
прямої, визначають єдину
площину. Знайдемо рівняння площини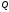 ,
що
проходить через три
дані точки,
,
що
проходить через три
дані точки,
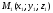 ,
,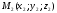 і
і
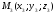 ,
не лежачі на одній прямій.
,
не лежачі на одній прямій.
Візьмемо
на площині довільну точку
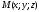 і складемо вектори
і складемо вектори
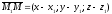 ,
,
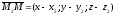 ,
,
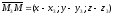 .
Ці вектори лежать на площині
.
Ці вектори лежать на площині
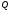 отже, вони компланарні. Використовуємо
умову компланарності трьох векторів
(їх змішаний добуток дорівнює нулю),
одержуємо
отже, вони компланарні. Використовуємо
умову компланарності трьох векторів
(їх змішаний добуток дорівнює нулю),
одержуємо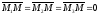 ,
тобто
,
тобто
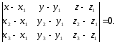 (12.6)
(12.6)
Рівняння (12.6) є рівняння площини, що проходить через три дані точки.
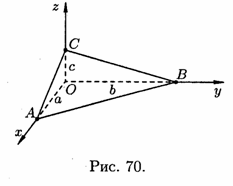
Рівняння площини у відрізках
Нехай
площина відсікає на осях
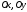 і
і
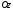 відповідно відрізки
відповідно відрізки
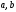 і
с
тобто проходить через три точки
і
с
тобто проходить через три точки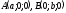 і
і
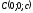 (див. рис. 70).
(див. рис. 70).
Підставляючи координати цих точок в рівняння (12.6), отримуємо
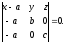
Розкривши
детермінант, маємо,
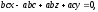 тобто .
тобто .
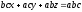 або
або
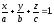 (12.7)
(12.7)
Рівняння (12.7) називається рівнянням площини у відрізках на осях. Їм зручно користуватися при побудові площини.
Нормальне рівняння площини
Положення
площини
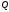 цілком визначається заданням одиничного
вектора
цілком визначається заданням одиничного
вектора
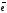 ,
що має напрям перпендикуляра
,
що має напрям перпендикуляра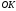 ,
опущеного на площину з початку координат,
і завдовжки
,
опущеного на площину з початку координат,
і завдовжки
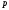 цього перпендикуляра (див. рис. 71).
цього перпендикуляра (див. рис. 71).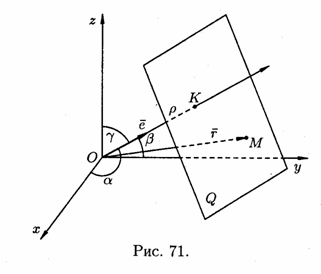
Нехай,
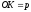 ,
а
,
а
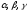 — кути, утворені
одиничним
вектором
— кути, утворені
одиничним
вектором
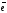 з осями
з осями
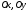 і
і
 .
Тоді
.
Тоді
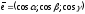 .
Візьмемо
на площині довільну точку
.
Візьмемо
на площині довільну точку
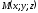 і з'єднаємо її з початком координат.
Утворюємо вектор
і з'єднаємо її з початком координат.
Утворюємо вектор
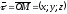 .
.
При
будь-якому положенні точки
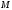 на площині
на площині
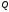 проекція радіус-вектора
проекція радіус-вектора
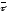 на напрям вектора
на напрям вектора
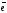 завжди рівно
завжди рівно
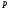 :
: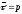 ,
тобто
,
тобто
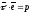 або
або
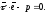 (12.8)
(12.8)
Рівняння
(12.8) називається нормальним
рівнянням площини у векторній
формі. Знаючи
координати векторів
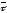 і,
і,
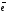 рівняння
(12.8) перепишемо у вигляді
рівняння
(12.8) перепишемо у вигляді
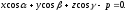 (12.9)
(12.9)
Рівняння (12.9) називається нормальним рівнянням площини в координатній формі.
Відзначимо,
що загальне рівняння площини (12.4) можна
привести до нормального рівняння
(12.9) так, як це робилося для рівняння
прямої на
площині. А саме: помножити обидві частини
рівняння (12.4) на нормуючий множник
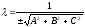 ,
де знак береться протилежним
знаку
вільного члена
,
де знак береться протилежним
знаку
вільного члена
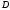 загального рівняння площини.
загального рівняння площини.
Площина. Основні задачі
Кут між двома площинами. Умови паралельності і перпендикулярності двох площин
Нехай
задано дві площини
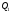 і
і
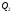 :
:
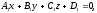
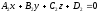 .
.
Під
кутом
між
площинами
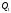 і
і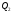 розуміється один з двогранних кутів,
утворених цими площинами.
розуміється один з двогранних кутів,
утворених цими площинами.
Кут
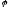 між нормальними векторами
між нормальними векторами
 і
і
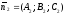 площин
площин
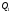 і
і
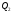 рівний одному з цих кутів (див. рис. 72).
Тому
рівний одному з цих кутів (див. рис. 72).
Тому
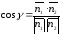 або
або
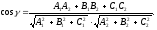
Для
знаходження гострого кута
слід узяти модуль правої частини.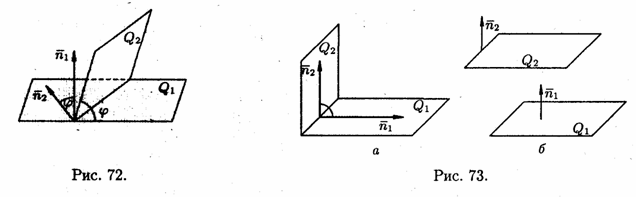
Якщо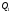 і
і
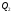 площини перпендикулярні (див. рис. 73,
а), то такі ж їх нормалі, тобто
площини перпендикулярні (див. рис. 73,
а), то такі ж їх нормалі, тобто
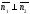 (і навпаки). Але тоді,
(і навпаки). Але тоді,
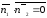 тобто
тобто
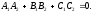 Отримана рівність є умова перпендикулярності
двох площин
Отримана рівність є умова перпендикулярності
двох площин
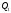 і
і
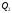 .
.
![]()
![]()
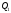 і
і
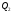 паралельні (див. рис. 73, б), то паралельні
і їх нормалі
паралельні (див. рис. 73, б), то паралельні
і їх нормалі
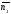 і
і
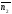 (і навпаки). Але тоді, як відомо, координати
векторів пропорційні:
(і навпаки). Але тоді, як відомо, координати
векторів пропорційні:
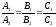 . Це і є умова паралельності площин
. Це і є умова паралельності площин
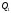 і
і
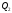 .
.
