
- •Рівняння площини в просторі
- •Загальне рівняння площини
- •Відстань від точки до площини
- •Рівняння прямої в просторі
- •2) Перетворення в нуль одного із знаменників рівнянь (12.13) означає перетворення в куль відповідного чисельника.
- •Умова, при якій дві прямі лежать в одній площині
- •Циліндричні поверхні
- •Нехай в площині лежить деяка лінія, рівняння якої (12.21)
- •Перетини твірної з еліпсом будуть. Виключимо, і з цих рівнянь і рівняння
- •4.1.9 Канонічні рівняння поверхонь другого порядку
- •Однопорожнинний гіперболоїд
- •Гіперболічний параболоїд
- •Конус другого порядку
Умова, при якій дві прямі лежать в одній площині
Нехай
прямі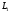 і
і
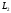 задані канонічними рівняннями
задані канонічними рівняннями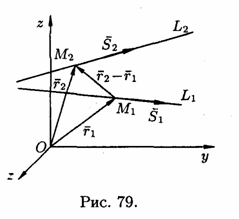
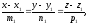
і
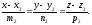
Рис. 79.
Їх
направляючі вектори відповідно
 і
і
 (див. рис. 79).
(див. рис. 79).
Пряма
 проходить через точку
проходить через точку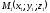 ,радіус-вектор
якої позначимо через
,радіус-вектор
якої позначимо через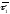 ; пряма
; пряма
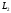 проходить
через точку
проходить
через точку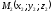 ,
радіус-вектор якої позначимо через
,
радіус-вектор якої позначимо через
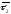 .
Тоді
.
Тоді
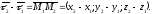
Прямі
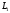 і
і
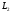 лежать в одній площині, якщо вектори
лежать в одній площині, якщо вектори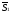 ,
,
 і
і
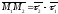 компланарні. Умовою компланарності
векторів є рівність нулю їх мішаного
добутку:
компланарні. Умовою компланарності
векторів є рівність нулю їх мішаного
добутку:
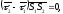 тобто
тобто
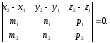
При
виконанні цієї умови прямі
 і
і
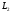 лежать
в одній площині, тобто або перетинаються,
якщо
лежать
в одній площині, тобто або перетинаються,
якщо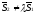 ,
або паралельні, якщо
,
або паралельні, якщо
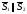 .
.
Пряма і площина в просторі. Основні задачі
Кут між прямою і площиною. Умови паралелі і перпендикулярності прямої і площини
Нехай
площина
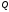 задана рівнянням
задана рівнянням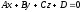 ,
а пряма
,
а пряма
 рівняннями
рівняннями
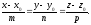
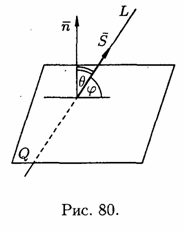
Рис.
80. кут між площиною
кут між площиною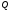 і прямою
і прямою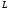 ,
а через
,
а через
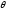 — кут між векторами
— кут між векторами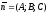 і
і
 (див. рис. 80). Тоді
(див. рис. 80). Тоді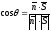 . При цьому :
. При цьому :
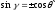 якщо
якщо то
то
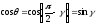 якщо
якщо то
то

(12.17)
Гострий
кут між площиною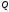 і прямою
і прямою
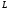 можна знайти, узявши у формулі (12.17)
модуль правої частини.
можна знайти, узявши у формулі (12.17)
модуль правої частини.
Якщо
пряма
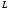 паралельна площин
паралельна площин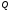 і,
то вектори
і,
то вектори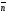 і
і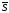 перпендикулярні (див. рис. 81), а тому
перпендикулярні (див. рис. 81), а тому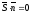 ,
тобто
,
тобто

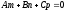
є
умовою
паралельності
прямої і площини.
Якщо
пряма
 перпендикулярна площині
перпендикулярна площині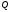 ,
то вектори
,
то вектори
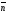 і
і
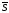 паралельні (див. рис. 82). Тому рівність
паралельні (див. рис. 82). Тому рівність
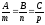
є умовами перпендикулярності прямої і площини.
Перетин прямої з площиною. Умова приналежності прямої площини
Нехай вимагається знайти точку перетину прямої
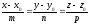 (12.18)
(12.18)
з
площиною
 (12.19)
(12.19)
Для цього треба вирішити систему рівнянь (12.18) і (12.19). Простіше всього це зробити, записавши рівняння прямої (12.18) в параметричному вигляді:
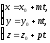
Підставляючи
ці вирази для
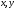 і
і
 в рівняння площини (12.19), одержуємо
рівняння
в рівняння площини (12.19), одержуємо
рівняння
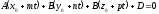 або
або
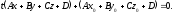 (12.20)
(12.20)
Якщо
пряма
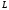 не паралель площині, тобто якщо
не паралель площині, тобто якщо
 то
з рівності (12.20) знаходимо значення
то
з рівності (12.20) знаходимо значення
 :
:

Підставляючи
знайдене значення t
в
параметричні рівняння прямої, знайдемо
координати точки перетину прямої з
площиною. Розглянемо тепер випадок,
коли

 :
:
а)
якщо
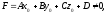 то
пряма
то
пряма
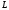 паралель площині і перетинати її не
буде (рівняння (12.20) рішення не має,
оскільки має вигляд
паралель площині і перетинати її не
буде (рівняння (12.20) рішення не має,
оскільки має вигляд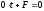 ,
де
,
де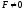 );
);
б)
якщо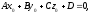 то рівняння (12.20) має вигляд
то рівняння (12.20) має вигляд йому
задовольняє будь-яке значення
йому
задовольняє будь-яке значення
 ,
будь-яка точка прямої є точкою перетину
прямої і площини. Висновок: пряма лежить
в площині. Таким чином, одночасне
виконання рівності
,
будь-яка точка прямої є точкою перетину
прямої і площини. Висновок: пряма лежить
в площині. Таким чином, одночасне
виконання рівності

є умовою приналежності прямої площини.
Циліндричні поверхні
Поверхня,
утворена рухом прямої ,
яка переміщається в
просторі, зберігаючи постійний напрям
і перетинаючи кожного разу деяку
криву
,
яка переміщається в
просторі, зберігаючи постійний напрям
і перетинаючи кожного разу деяку
криву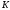 ,
називається
циліндричною поверхнею
або
циліндром.
При
цьому крива К
називається
направляючою
циліндра,
а пряма
,
називається
циліндричною поверхнею
або
циліндром.
При
цьому крива К
називається
направляючою
циліндра,
а пряма
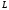 — його твірної (див. рис. 83).
— його твірної (див. рис. 83).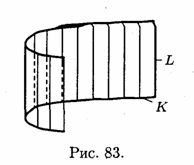
Розглядатимемо циліндричні поверхні, що направляють яких лежать в одній з координатних площин, а твірні паралелі координатної осі, перпендикулярній цій площині.
