
- •Лекція 5
- •1. Збіжні послідовності
- •2. Властивості збіжних послідовностей
- •3. Невизначені вирази. Теорема Штольца
- •Лекція 6
- •1. Граничний перехід у нерівностях
- •2. Монотонні послідовності
- •3. Число е
- •Лекція 7
- •1. Теорема про вкладені відрізки
- •3. Теорема Больцано-Вейєрштрасса
- •4. Критерій Коші збіжності числової послідовності. Фундаментальна послідовність
- •Лекція 8
- •1. Поняття метричного простору
- •2. Повні метричні простори.
- •3. Доповнення простору.
- •Питання для самостійного опрацювання
- •Функції однієї змінної
- •2. Класифікація функцій
- •3. Елементарні функції.
- •Тема 3. Границя функції однієї змінної лекція 9
- •1. Границя функції. Означення границі функції за Гейне й за Коші.
- •2. Односторонні границі
- •3. Границя функції на нескінченності
- •4.Теореми про границі функцій
- •Лекція 10
- •1. Визначні границі
- •2. Нескінченно малі й нескінченно великі функції
- •3. Порівняння нескінченно малих функцій. Еквівалентні нескінченно малі функції.
2. Односторонні границі
Число
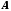 називається границею функції
називається границею функції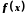 у точці
у точці справа (зліва), якщо для будь-якої збіжної
до
справа (зліва), якщо для будь-якої збіжної
до послідовності
послідовності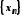 ,
елементи якої більші (менші)
,
елементи якої більші (менші)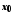 ,
відповідна послідовність
,
відповідна послідовність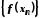 збігається до числа
збігається до числа .
.
Символічно це записують так:
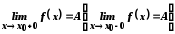 .
.
Можна дати
рівносильне означення односторонніх
границь функції "в термінах
 ".
".
Число
 називається границею функції
називається границею функції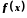 у точці
у точці
 справа (зліва), якщо для довільного числа
справа (зліва), якщо для довільного числа
 існує таке
існує таке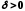 ,
що для всіх
,
що для всіх ,
які задовольняють умову
,
які задовольняють умову ,
виконується нерівність
,
виконується нерівність .
.
Теорема.
Функція
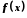 має в точці
має в точці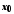 границю тоді й тільки тоді, коли в цій
точці існує як права, так і ліва границя
та ці границі рівні між собою. У цьому
випадку границя функції дорівнює
одностороннім границям.
границю тоді й тільки тоді, коли в цій
точці існує як права, так і ліва границя
та ці границі рівні між собою. У цьому
випадку границя функції дорівнює
одностороннім границям.
Доведення.
Нехай у
точці
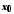 існують односторонні границі функції
існують односторонні границі функції
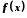 і
і
 .
Тоді, згідно з означенням односторонніх
границь, для будь-якого
.
Тоді, згідно з означенням односторонніх
границь, для будь-якого
 існують числа
існують числа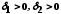 ,
такі, що для всіх
,
такі, що для всіх ,
які задовольняють умову
,
які задовольняють умову ,
і для всіх
,
і для всіх ,
котрі задовольняють умову
,
котрі задовольняють умову ,
виконується нерівність
,
виконується нерівність .
Виберемо
.
Виберемо .
Тоді для всіх
.
Тоді для всіх ,
що задовольняють умову
,
що задовольняють умову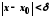 ,
виконуватиметься нерівність
,
виконуватиметься нерівність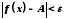 .
Тобто
.
Тобто .
З іншого боку, якщо
.
З іншого боку, якщо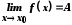 ,
то в точці
,
то в точці існують односторонні границі й
існують односторонні границі й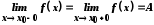 .
.
3. Границя функції на нескінченності
Число
 називається границею функції
називається границею функції при
при , якщо для будь-якої нескінченно великої
послідовності
, якщо для будь-якої нескінченно великої
послідовності значень аргументу відповідна послідовність
значень аргументу відповідна послідовність значень функції збігається до числа
значень функції збігається до числа .
.
Символічно це
записують так:
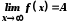 .
.
Число
 називається границею функції
називається границею функції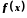 при
при , якщо для будь-якої нескінченно великої
послідовності
, якщо для будь-якої нескінченно великої
послідовності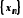 ,
елементи
,
елементи![]() якої додатні (від'ємні), відповідна
послідовність
якої додатні (від'ємні), відповідна
послідовність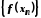 значень функції збігається до числа
значень функції збігається до числа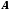 .
.
Символічно це записують так:
 .
.
Можна дати означення
"в термінах
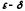 ",
рівносильні наведеним вище.
",
рівносильні наведеним вище.
4.Теореми про границі функцій
Теорема.
Якщо функція
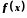 має границю в точці
має границю в точці
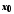 ,
то ця границя єдина.
,
то ця границя єдина.
Доведення.
Припустимо, що функція
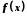 має дві
різні границі
має дві
різні границі
 .
Виберемо з області визначення функції
.
Виберемо з області визначення функції довільну послідовність
довільну послідовність ,
збіжну до
,
збіжну до .
Тоді послідовність
.
Тоді послідовність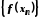 ,
згідно з означенням границі функції,
матиме дві різні границі
,
згідно з означенням границі функції,
матиме дві різні границі ,
що неможливо, оскільки будь-яка збіжна
послідовність має єдину границю.
,
що неможливо, оскільки будь-яка збіжна
послідовність має єдину границю.
Теорема.
Якщо функції
 і
і
 мають у точці
мають у точці границі, тофункції
границі, тофункції
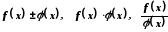 (при
(при
 )
у точці
)
у точці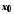 також мають границі, причому
також мають границі, причому
 ;
(3)
;
(3)
 ;
(4)
;
(4)
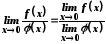 .
(5)
.
(5)
Доведення.
Нехай послідовність
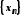
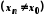 – довільна збіжна до
– довільна збіжна до послідовність значень аргументу функцій
послідовність значень аргументу функцій і
і .
Тоді відповідні послідовності
.
Тоді відповідні послідовності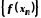 і
і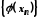 збіжні й
за властивостями збіжних послідовностей
збіжні й
за властивостями збіжних послідовностей
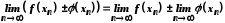 ;
;
 ;
;
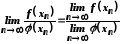 (де
(де
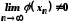 ).
).
Отже, згідно з означенням границі функції мають місце співвідношення 3-5.
Теорема .
Нехай функції
 і
і
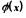 ,
визначені в деякому околі точки
,
визначені в деякому околі точки
 ,
крім, можливо, самої точки
,
крім, можливо, самої точки ,
мають у точці
,
мають у точці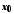 границі, й такі, що в околі точки
границі, й такі, що в околі точки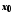
 .
Тоді
.
Тоді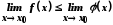 .
.
Доведення.
Виберемо в околі точки
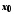 довільну збіжну до
довільну збіжну до послідовність
послідовність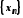
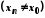 .
Тоді послідовності
.
Тоді послідовності і
і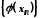 збіжні й
збіжні й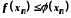 .
Тому за відповідною властивістю збіжних
послідовностей
.
Тому за відповідною властивістю збіжних
послідовностей .
.
Звідси,
за означенням границі функції в точці,
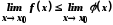 .
.
Наслідок.
Якщо в деякому околі
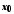 ,
крім, можливо, самої точки
,
крім, можливо, самої точки ,
виконується нерівність
,
виконується нерівність і функція
і функція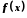 у точці
у точці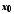 має границю, то
має границю, то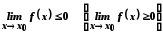 .
.
Теорема
3.5.
Нехай
функції
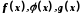 визначені в деякому околі точки
визначені в деякому околі точки
 ,
крім, можливо, самої точки
,
крім, можливо, самої точки ,функції
,функції
 мають у точці
мають у точці
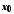 границю, рівну
границю, рівну ,
тобто
,
тобто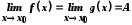 .
Нехай, крім того, виконується нерівність
.
Нехай, крім того, виконується нерівність .
Тоді функція
.
Тоді функція![]() у точці
у точці має границю, рівну
має границю, рівну ,
тобто
,
тобто .
.
Доведення.
Нехай
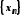
 – довільна збіжна до
– довільна збіжна до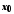 послідовність. Послідовності
послідовність. Послідовності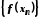 і
і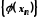 відповідних значень функції
відповідних значень функції збіжні, й
збіжні, й .
Оскільки
.
Оскільки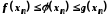 ,
то згідно з відповідною властивістю
збіжних послідовностей
,
то згідно з відповідною властивістю
збіжних послідовностей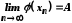 .
Отже, за означенням границі функції в
точці
.
Отже, за означенням границі функції в
точці .
.
Зауваження.
Наведені вище теореми про границі мають
місце і для випадків
 .
.
