
- •Лекція 5
- •1. Збіжні послідовності
- •2. Властивості збіжних послідовностей
- •3. Невизначені вирази. Теорема Штольца
- •Лекція 6
- •1. Граничний перехід у нерівностях
- •2. Монотонні послідовності
- •3. Число е
- •Лекція 7
- •1. Теорема про вкладені відрізки
- •3. Теорема Больцано-Вейєрштрасса
- •4. Критерій Коші збіжності числової послідовності. Фундаментальна послідовність
- •Лекція 8
- •1. Поняття метричного простору
- •2. Повні метричні простори.
- •3. Доповнення простору.
- •Питання для самостійного опрацювання
- •Функції однієї змінної
- •2. Класифікація функцій
- •3. Елементарні функції.
- •Тема 3. Границя функції однієї змінної лекція 9
- •1. Границя функції. Означення границі функції за Гейне й за Коші.
- •2. Односторонні границі
- •3. Границя функції на нескінченності
- •4.Теореми про границі функцій
- •Лекція 10
- •1. Визначні границі
- •2. Нескінченно малі й нескінченно великі функції
- •3. Порівняння нескінченно малих функцій. Еквівалентні нескінченно малі функції.
3. Невизначені вирази. Теорема Штольца
Нехай
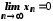 і
і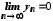 .
Виникає питання, що можна сказати про
границю
.
Виникає питання, що можна сказати про
границю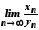 ?
Виявляється, що ця границя залежно від
окремого закону поведінки змінних
?
Виявляється, що ця границя залежно від
окремого закону поведінки змінних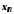 та
та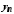 може приймати різні значення або взагалі
не існувати.
може приймати різні значення або взагалі
не існувати.
Приклади.
1. Якщо
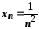 і
і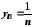 ,
то
,
то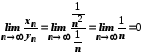 .
.
2. Якщо
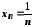 і
і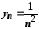 ,
то
,
то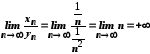 .
.
3. Якщо
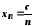 і
і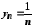 ,
то
,
то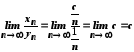 .
.
4. Якщо
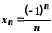 і
і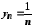 ,
то
,
то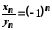 та
та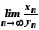 не існує.
не існує.
Отже, лише значення
границь числових послідовностей
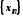 ,
,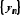 не дозволяє у розглянутому вище випадку
робити висновки про значення границі
їх відношення. Для того, щоб схарактеризувати
цю особливість, говорять, що за умови
не дозволяє у розглянутому вище випадку
робити висновки про значення границі
їх відношення. Для того, щоб схарактеризувати
цю особливість, говорять, що за умови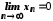 і
і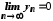 вираз
вираз
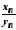 є невизначеністю типу
є невизначеністю типу
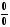 .
.
Аналогічно невизначеними виразами є:
а) у випадку
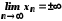 і
і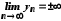 вираз
вираз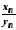 є невизначеністю типу
є невизначеністю типу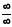 ;
;
б) у випадку
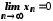 і
і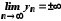 вираз
вираз
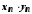 є
невизначеністю типу
є
невизначеністю типу
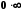 ;
;
в) у випадку
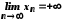 та
та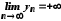 вираз
вираз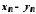 є невизначеністю типу
є невизначеністю типу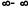 .
.
Для визначення
границь невизначених виразів
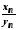 типу
типу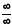 часто може застосовуватися теорема
Штольца, яку ми наведемо без доведення
часто може застосовуватися теорема
Штольца, яку ми наведемо без доведення
Теорема.
Якщо послідовності
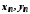 такі,
що
такі,
що
1) починаючи з
деякого номера
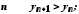
2)
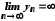 ;
;
3) існує
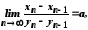
то
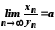 .
.
Лекція 6
Граничний перехід у нерівностях.
Монотонні послідовності.
Число е.
1. Граничний перехід у нерівностях
Теорема
. Якщо
елементи збіжної послідовності
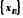 ,
починаючи з деякого номера
,
починаючи з деякого номера ,
задовольняють нерівність
,
задовольняють нерівність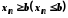 ,
то і границя цієї послідовності
задовольняє нерівність
,
то і границя цієї послідовності
задовольняє нерівність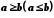 .
.
Доведення.
Нехай, починаючи з деякого номера
 ,
елементи збіжної послідовності
,
елементи збіжної послідовності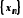 задовольняють нерівність
задовольняють нерівність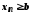 і
і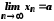 .
Припустимо, що
.
Припустимо, що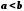 .
Оскільки
.
Оскільки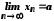 ,
то для
,
то для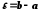 існує номер
існує номер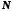 такий, що для
такий, що для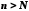 виконується нерівність
виконується нерівність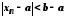 ,
яка рівносильна нерівності
,
яка рівносильна нерівності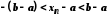 .
Тоді із нерівності
.
Тоді із нерівності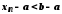 одержуємо:
одержуємо: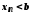 ,
що суперечить умові. Отже,
,
що суперечить умові. Отже,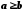 .
.
Випадок
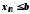 доводиться аналогічно.
доводиться аналогічно.
Наслідок
1. Якщо
елементи збіжних послідовностей
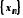 і
і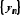 ,
починаючи з деякого номера
,
починаючи з деякого номера ,
задовольняють нерівність
,
задовольняють нерівність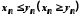 ,
то
,
то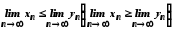 .
.
Нехай, починаючи
з деякого номера, виконується нерівність
![]() .
Тоді для таких
.
Тоді для таких
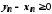 .
Отже,
.
Отже,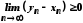 ,
а тому
,
а тому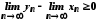 .
Звідси маємо
.
Звідси маємо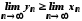 .
Другий випадок установлюється аналогічно.
.
Другий випадок установлюється аналогічно.
Теорема.
Нехай члени послідовностей
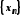 ,
,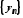 ,
,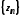 ,
починаючи з деякого номера, задовольняють
нерівність
,
починаючи з деякого номера, задовольняють
нерівність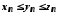 і
і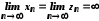 .
Тоді послідовність
.
Тоді послідовність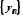 збіжна й
збіжна й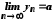 .
.
Доведення.
Задамо довільне число
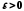 .
Тоді для заданого
.
Тоді для заданого знайдеться такий номер
знайдеться такий номер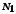 ,
що для
,
що для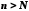 виконуватиметься нерівність
виконуватиметься нерівність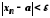 ,
тобто
,
тобто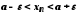 .
Для цього ж
.
Для цього ж знайдеться такий номер
знайдеться такий номер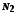 ,
що
,
що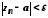 для
для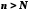 ,
тобто
,
тобто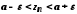 .
.
Виберемо
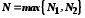 .
Тоді виконуватиметься нерівність
.
Тоді виконуватиметься нерівність
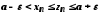
для всіх
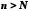 .
.
Ураховуючи умову
теореми, маємо
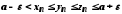
або
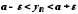 ,
тобто
,
тобто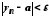 для всіх
для всіх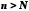 .
Звідси випливає, що
.
Звідси випливає, що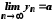 .
.
2. Монотонні послідовності
Послідовність
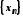 називається неспадною ( незростаючою
), якщо виконується нерівність
називається неспадною ( незростаючою
), якщо виконується нерівність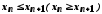 для усіх
для усіх .
.
Неспадні та незростаючі послідовності називаються монотонними.
Якщо для всіх
членів монотонної послідовності
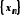 виконується строга нерівність
виконується строга нерівність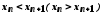 ,
то послідовність називається зростаючою
(спадною). Зростаючі та спадні послідовності
називаються також строго монотонними.
,
то послідовність називається зростаючою
(спадною). Зростаючі та спадні послідовності
називаються також строго монотонними.
З означення випливає, що монотонні послідовності обмежені принаймні з однієї сторони: неспадна обмежена знизу, а незростаюча – зверху.
Теорема. Монотонна обмежена послідовність збіжна.
Доведення.
Розглянемо випадок неспадної послідовності
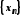 .
.
Отже, нехай для
усіх
 виконуються наступні умови:
виконуються наступні умови:
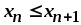 ;
;існує таке число
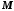 ,
що
,
що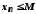 .
.
Розглянемо числову
множину
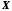 ,
яка складається з усіх елементів
послідовності
,
яка складається з усіх елементів
послідовності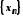 .
За умовою ця множина непорожня і обмежена
зверху, а тому має точну верхню межу.
.
За умовою ця множина непорожня і обмежена
зверху, а тому має точну верхню межу.
Позначимо
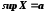 .
Покажемо, що
.
Покажемо, що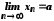 .
.
Оскільки
 -
точна верхня межа елементів послідовності
-
точна верхня межа елементів послідовності
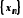 ,
то, згідно з властивістю точної верхньої
межі, для будь-якого
,
то, згідно з властивістю точної верхньої
межі, для будь-якого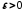 існує номер
існує номер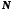 такий, що
такий, що
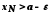 .
Так як послідовність
.
Так як послідовність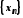 неспадна, то при
неспадна, то при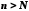 виконується нерівність
виконується нерівність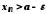 .
З іншого боку, згідно з означенням точної
верхньої межі,
.
З іншого боку, згідно з означенням точної
верхньої межі,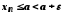 для всіх
для всіх .
Таким чином, при
.
Таким чином, при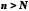 маємо нерівність
маємо нерівність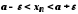 ,
тобто
,
тобто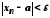 при
при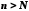 .
Отже,
.
Отже,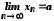 .
.
Для випадку незростаючої послідовності доведення аналогічне.
*** Із теорем 2.5** і 2.8** випливає, що обмеженість монотонної послідовності є необхідною і достатньою умовою її збіжності.
