4.1.2. Геометричний зміст похідної

Означення. Дотичною до кривої L у точці М називається граничне положення МN січної ММ₁ при прямуванні точки М₁ по кривій L до точки М (рис. 4.1).

Нехай крива, задана рівнянням , має дотичну в точціМ (х, у). Позначимо (рис. 4.2) кутовий коефіцієнт дотичної МN: . Надамо в точціх приросту , тоді ординатау набуде приросту .

З випливає, що. Коли, тоі січна прямує до положення дотичноїМN.

Таким чином, .

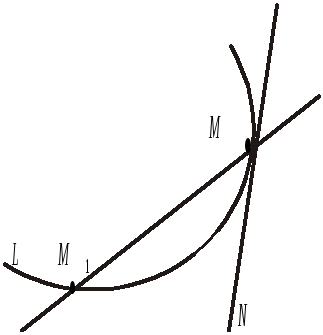
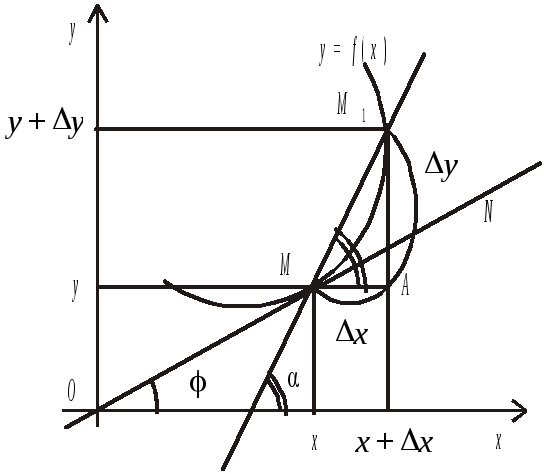
Рис. 4.1 Рис. 4.2

Оскільки , то тобто похідна чисельно дорівнює кутовому коефіцієнту дотичної, проведеної до графіка функції у точці з абсцисою х. У цьому полягає геометричний зміст похідної.

Нехай рівняння прямої, що проходить через задану точку М₀ (х₀; у₀) у даному напрямі (рис. 4.4):

, Оскільки, то з виразу (4.2) ді- станемо рівняння дотичної у вигляді

.

Нормаллю до графіка функції в точці М₀ називається перпендикуляр, проведений до дотичної в цій точці:

Для пояснення економічного змісту похідної розглянемо задачу про продуктивність праці. Нехай функція відображає кількість виробленої продукціїu за час t і необхідно знайти продуктивність праці в момент t₀.

За період часу від t₀ до кількість виробленої продукції зміниться від значеннядо значення; тоді середня продуктивність праці за цей період часу. Очевидно, що продуктивність праці в моментt₀ можна визначити як граничне значення середньої продуктивності за період часу від t₀ до при, тобто

.

Таким чином, продуктивність праці є похідна від обсягу вироб­леної продукції по часу.

Застосування диференціального числення для дослідження економічних об’єктів та процесів на основі аналізу цих граничних величин дістало назву граничного аналізу. Граничні величини характеризують не стан (як сумарна чи середня величини), а процес зміни економічного об’єкта. Таким чином, похідна виступає як швидкість зміни деякого економічного об’єкта (процесу) за часом або відносно іншого об’єкта дослідження. Але необхідно врахувати, що економіка не завжди має змогу використовувати граничні величини у зв’язку з неподільністю багатьох об’єктів економічних розрахунків та перервністю (дискретністю) економічних показників у часі (наприклад, річних, квартальних, мі- сячних та ін.). Водночас у деяких випадках можна знехтувати дискретністю показників і ефективно використовувати граничні величини.

54. Похідна складної та оберненої функцій

Похідна оберненої ф-ції х=φ(х) по змінній у дор. оберненій величині похіднохвід прямої ф-ції у=ƒ(х):.

55. Диференціювання параметрично заданих функцій

Нехай функцію відзадано параметричними рівняннями:

.

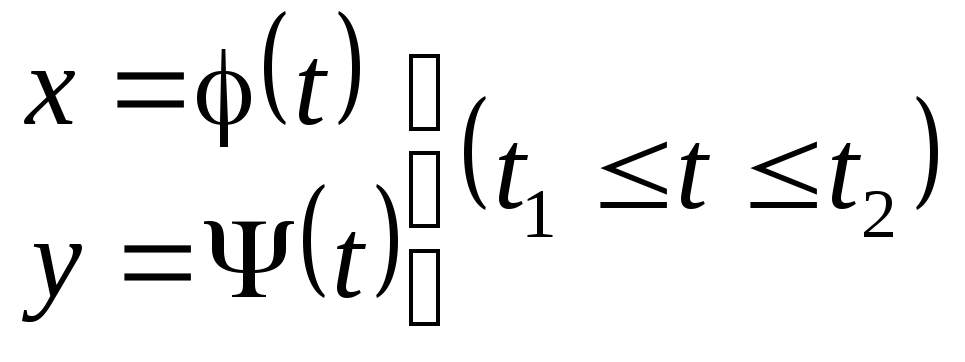Припустимо, що функції мають похідні і що функціямає обернену функцію, яка також є диференційовною. Тоді визначену параметричними рівняннями функціо- нальну залежністьможна розглядати як складну функцію,(— проміжний аргумент).

На підставі теорем 6 та 7 маємо:

, .

Звідки або.

Знайдена формула дає можливість знаходити похідну від параметрично заданої функції, не знаходячи явної залежності

56. Диференціювання неявно заданих функцій

Для знах. пох. ф-ції у, заданої неявно, дост. продиф. обидві част. р-ня, розгл. у як ф-цію від х, а потім із здобут. р-ня знайти пох. у’.

57. Похідна степенево-показникових функцій

Нехай є степ.-показн. ф-ція. Прологарифмуємо ліву і праву частину.. .Продиф. праву і ліву част.

58. Похідні вищих порядків

Пох. І порядку від пох. І порядку наз. пох. ІІ порядку. Познач. y’’. f’’(x).

Пох. n-ого порядку наз. пох. від пох. (n-1)-ого порядку y⁽ⁿ⁾=(y^(n-1))^’. Нехай ф-ція у’=f(x) диф на відрізку [a;b], тоді вона має диференціал. Дифер. n-го поряку dⁿy=f⁽ⁿ⁾(x)dxⁿ.

59. Диференціал та його властивості

Добуток називаєтьсядиференціалом функції у = f (х); його позначають символом dy, тобто

. Це головна лінійна відносно дельта х частина приросту ункції.

Властивості диференціала:

1. Диференціал сталої величини дорівнює 0: dc=0

2. Сталий множник можна виносити за знак диференціала: d(cu)=cdu

3. Диференціал суми дорівнює сумі диференціалів: d(u+-v)=du+-dv

4. Диференціал добутку дорівнює сумі добутку диференціала першого множника на другий множник та добутку диференціала другого множника на перший: duv=vdu+udv

5. Диференціал частки знаходиться за формулою:

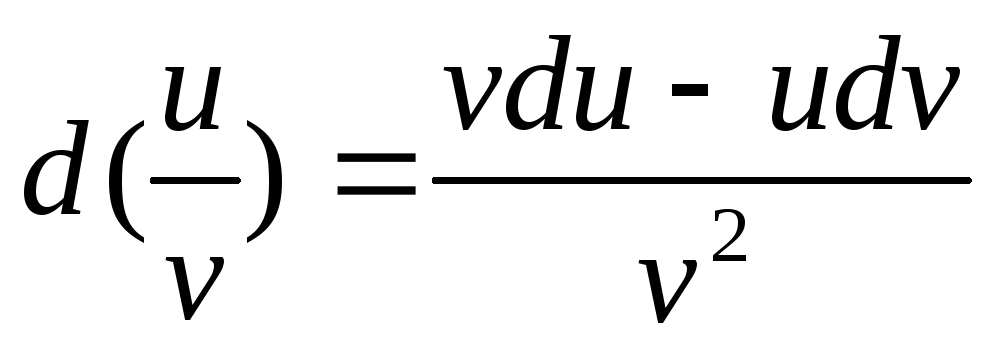
6. Диференціал складної функції: Нехай y=f(x), x=j(t)

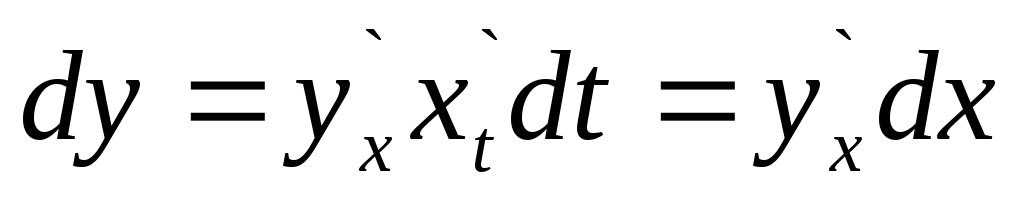
60. Застосування диференціала до наближених обчислень

61. Правило Лопіталя

Правило Лопіталя

Розглянемо відношення , де функціїівизначені й диференційовні в деякому околі точкиа, виключаючи, можливо, саму точку а. Може бути, що при обидві функціїіпрямують до 0 або до, тобто ці функції одночасно є нескінченно малими або нескінченно великими величинами при . Тоді говорять, що в точціа функція f (x) має невизначеність виду

. (4.17)

У цьому випадку, використовуючи похідні і, можна сформулювати правило для знаходження границі функціїf (x) при , тобто визначити спосіб для розкриття невизначеностей виду (4.17).

Теорема (правило Лопіталя). Границя відношення двох нескінченно малих або нескінченно великих функцій дорівнює границі відношення їхніх похідних (скінченній або нескінченній), якщо остання існує

62. Застосування правила Лопіталя у невизначеностях виду

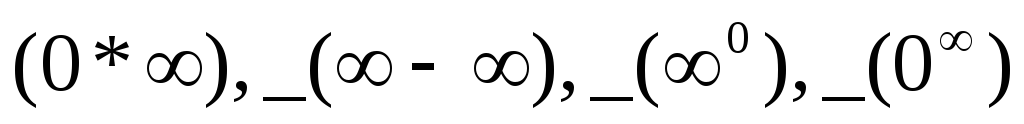
Невизначеність виду . Нехай.

Потрібно знайти

. (4.18)

Це невизначеність типу .

Якщо вираз (4.18) записати у вигляді

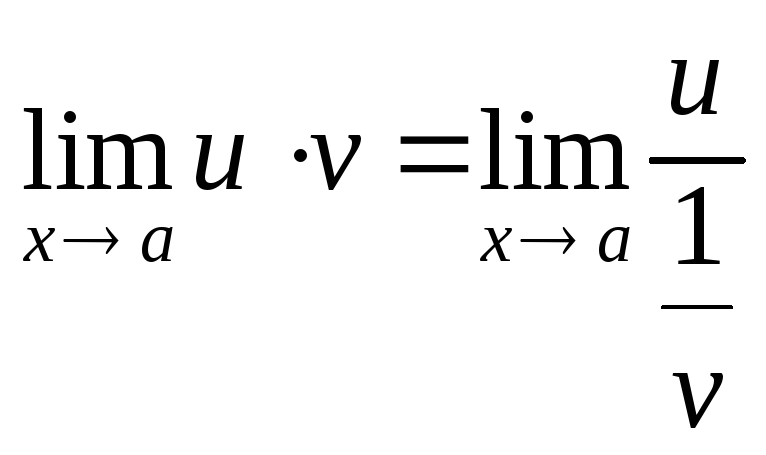або ,

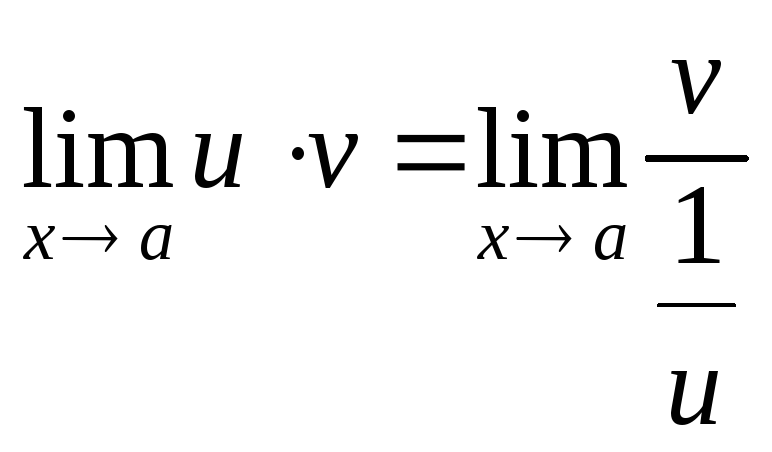то при дістанемо невизначеність відповідно виглядуабо.

Невизначеність . Якщо функціїпри(а — скінченне або нескінченне), то різниця при дає невизначеність. Остання з допомогою алгебраїч­них перетворень зводиться до невизначеності або.

Невизначеність вигляду . Нехай маємо функцію.

При (а — скінченне або нескінченне) можливі три випадки:

а) маємо невизначеність виду;

б) дістанемо невизначеність;

в) маємо невизначеність виду.

Ці невизначеності за допомогою логарифмування зводяться до невизначеності вигляду . Справді, позначимо дану функцію черезу, тобто візьмемо . Прологарифмувавши цю рівність, дістанемо.

Легко перевірити, що при добутокбуде невизначеністюдля всіх трьох випадків

Відповідно до підпункту 1 розкриємо невизначеність , тобто знайдемо границю(k — скінченне або ).

Звідси .

63. Необхідна і достатня ознаки зростання (спадання) функції

Необхідна ознака зростання (спадання) функції: якщо диференційована на деякому проміжку функція зростає (спадає) на цьому проміжку, то

Достатня ознака зростання (спадання) функції : якщо для всіх хє(a,b) то функція зростає (спадає) на проміжку (а,b)

64. Екстремум функції, необхідна та достатня умови існування екстремуму

Необхідна умова екстремуму функції. Теорема. У точ- ці екстремуму диференційовної функції похідна її дорівнює нулю:

Наслідок. Неперервна функція може мати екстремум тільки в тих точках, де похідна функції дорівнює нулю або не існує.

65. Опуклість та вгнутість графіка функції. Необхідна і достатня умови опуклості (вгнутості) графіка функції

Крива на проміжку називається опуклою (угнутою), якщо всі точки кривої лежать нижче (вище) будь-якої її дотичної на цьому проміжку.

Теорема 1. 1) Якщо в усіх точках проміжку (с, b) для функ­ції друга її похідна додатна, то графік функ­ції вгнутий.