3. Метод розділення змінних.

1. Знайти неперервний в замкнутій області розв’язок рівняння, що задовольняє початковій умові,та однорідним граничним умовам.

Для цього розглянемо допоміжну задачу:

2. знайти розв’язок рівняння тотожно не рівне 0, що задовольняє однорідним граничним умовам, та має вид.

Міркуючи як це робилось раніше отримаємо, що Х, Т – задовольняють рівнянням:

Як і раніше задовольняє 1, якщо.

Відповідно .

Повертаючись до першої задачі. Отримаємо, що розв’язок її має вигляд

Враховуючи початкову умову маємо

.

Відмітимо, що як і раніше, розв’язок, коли існуютьі відповідні ряди збігаються.

Згідно з [5], для цього достатньо щоб була неперервна ната мала частково­неперервну похідну.

Лекція №16. Перша крайова задача для рівняння параболічного виду

1. Неоднорідна задача з нульовими початковими і граничними умовами.

Розв’яжемо задачу:

Будемо шукати розв’язок у вигляді

.

Для цього представимо у вигляді ряду

, де .

Підставляючи у рівняння отримаємо

Отже

або

Із початкових даних для маємо

,

отже

Розв’язуючи звичайне диференційне рівняння з нульовими початковими даними, отримаємо

.

Таким чином, розв’язок має вид

2. Перша крайова задача.

Розв’яжемо задачу:

Введемо невідому функцію за допомогою рівності

де визначається як розв’язок рівняння, яке задовольняє умовам

Виберемо так, щоб, тобто.

Таким чином, задовольняє рівняння

Тоді, розв’язок - сума розв’язка рівняння з нульовою початковою умовою. (див. п.1) та розв’язку однорідного рівняння з початковою умовою заданою за допомогою функції(дивіться лекцію 7).

3. Задачі на нескінченій та напівнескінечній прямій.

1. Знайти обмежену функцію визначену на області, що задовольняє рівняннюі початковій умові.

Будемо шукати розв’язок в вигляді . Підставляючи в рівняння отримаємо

(- параметр).

Маємо рівняння для івідповідно

Розв’язуючи ці рівняння знайдемо частинний розв’язок вихідного рівняння

. Розглянемо функцію

(вона задовольняє рівняння, так як суперпозиція розв’язків – розв’язок). Вимагаючи виконання початкової умови при отримаємо

(із перетворення Фур’є) отримаємо

.

Підставляючи в , остаточно будемо мати

Таким чином ,

називається інтегралом Пуассона, неперервно примикає до (доведення дивіться [5]) і являється єдиним розв’язком задачі для будь якої обмеженої.

Приклад. Знайти розв’язок рівняння теплопровідності, якщо початкова температура постійна але різна для і

Користуючись формулою отримаємо

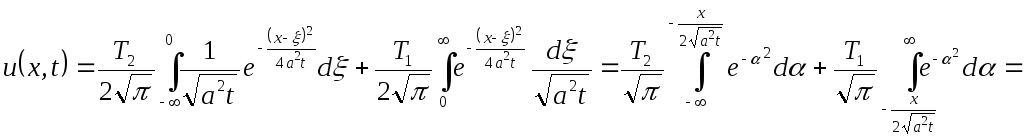
при підрахунку ми врахували наступні рівності

Для напівнескінечної прямої перша крайова задача має вид

Розв’язок має вид

дивіться [5]. Розглянути самостійно.

Приклад.

Найпростіша класична теорія охолодження Землі приводить до рівняння

, ,

- температура плавлення гірських порід,

- температура поверхні.

Розв’язок

Градієнт функції при дорівнює

Підставляючи сюди відомі значення геотермічного градієнту

- коефіцієнт температуропровідності базальтів і гранітів отримаємо для тривалості процесу охолодження значення років.

З відкриттям радіоактивного розпаду схема змінилась, рівняння прийняло вид

, , де

А – щільність теплових джерел. При цьому отримуємо рівним у 2 мільярди років. Дивіться більш докладніше [5].