Контрольна робота №5.

І. Знайти область розв’язків наступних систем нерівностей:

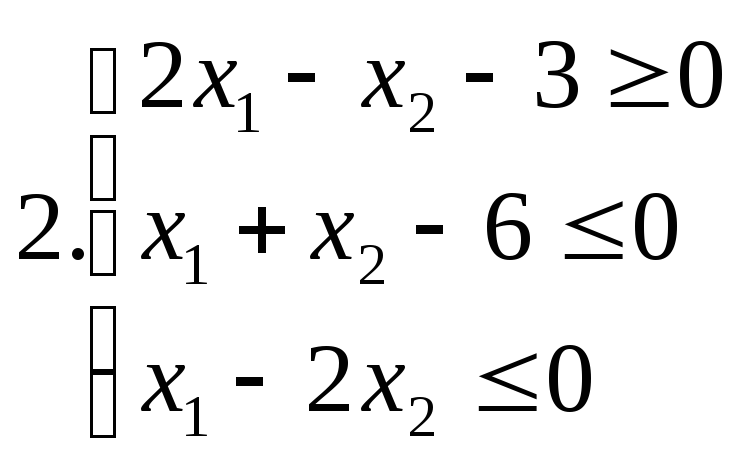
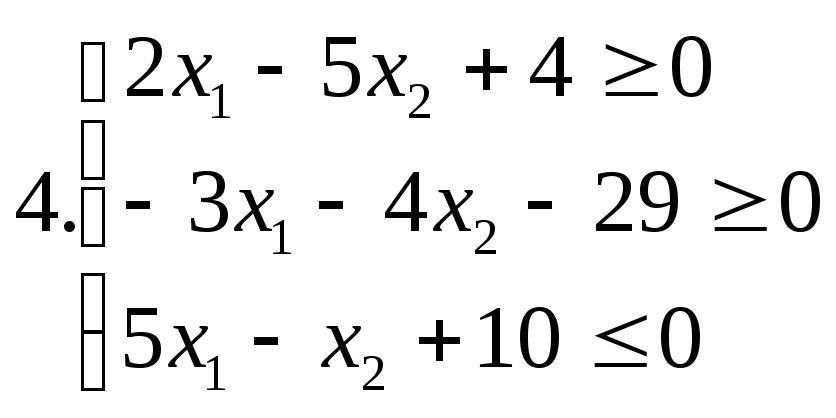
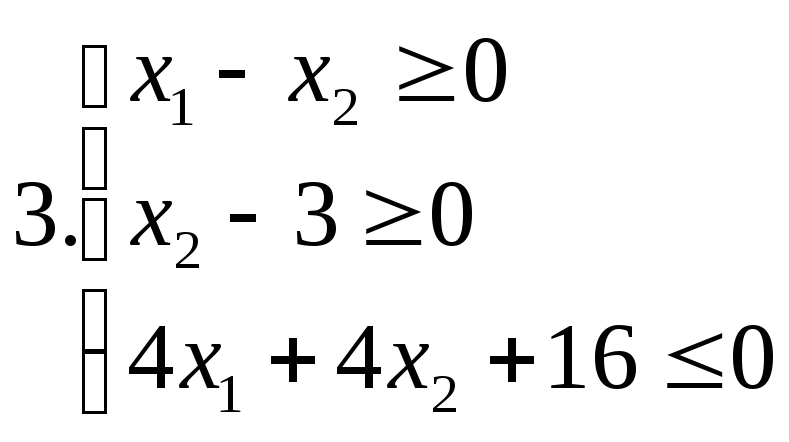
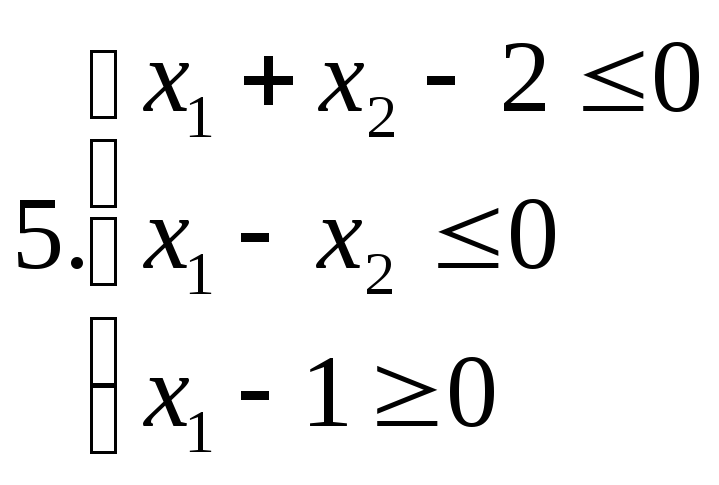
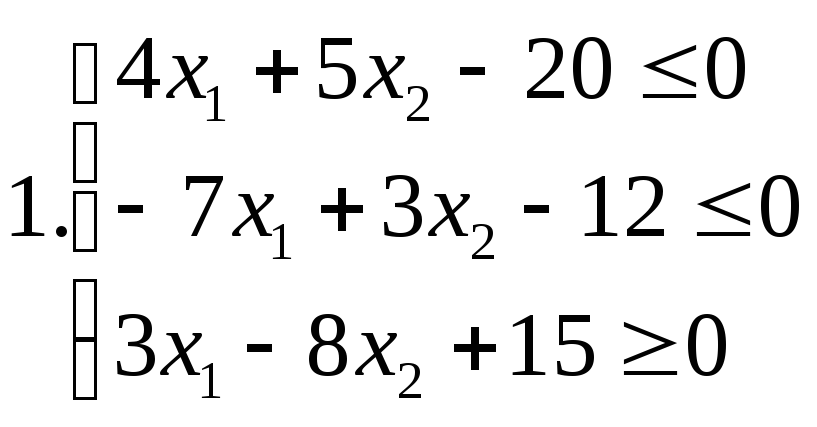
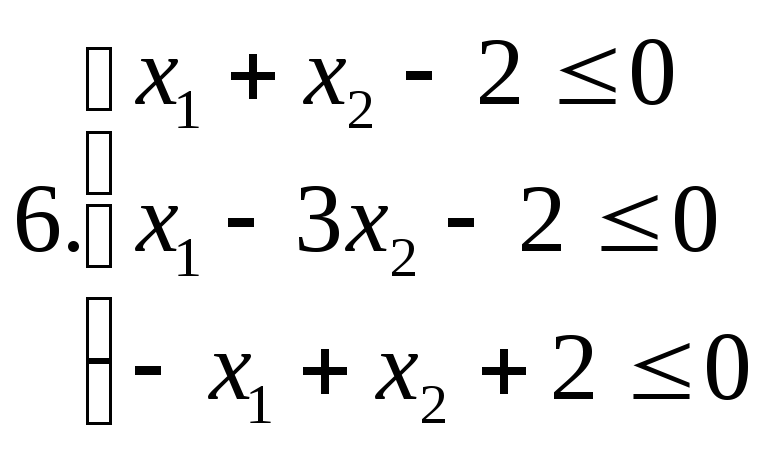
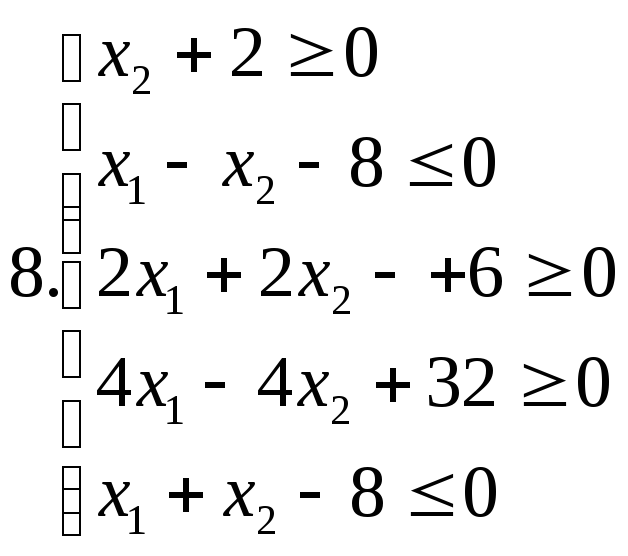
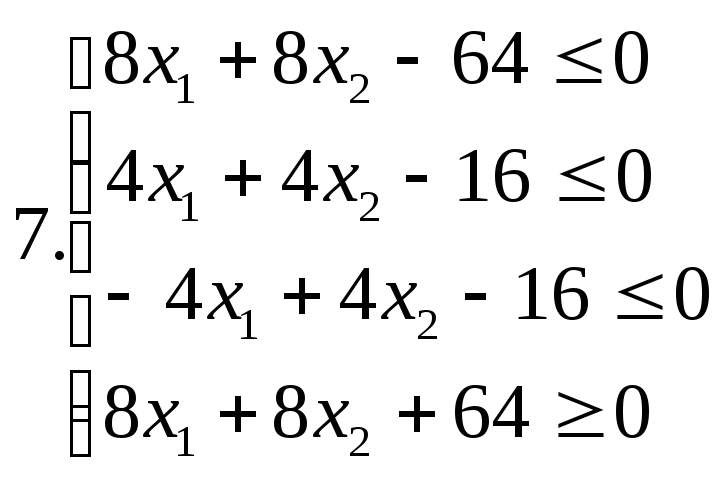
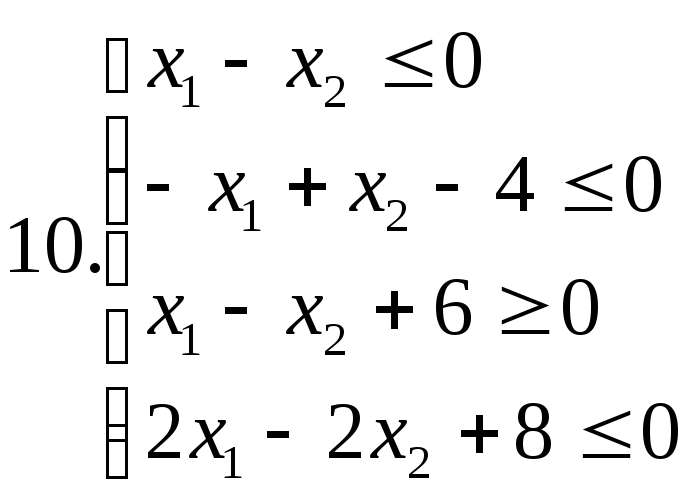
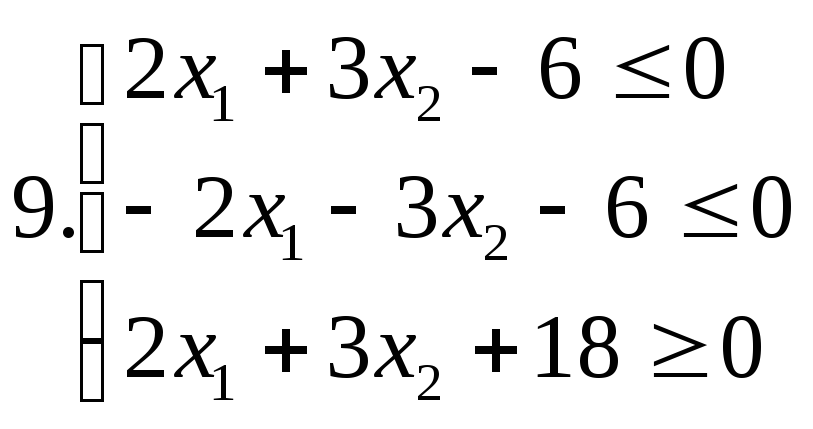
ІІ. Дана система лінійних нерівностей та функція f:

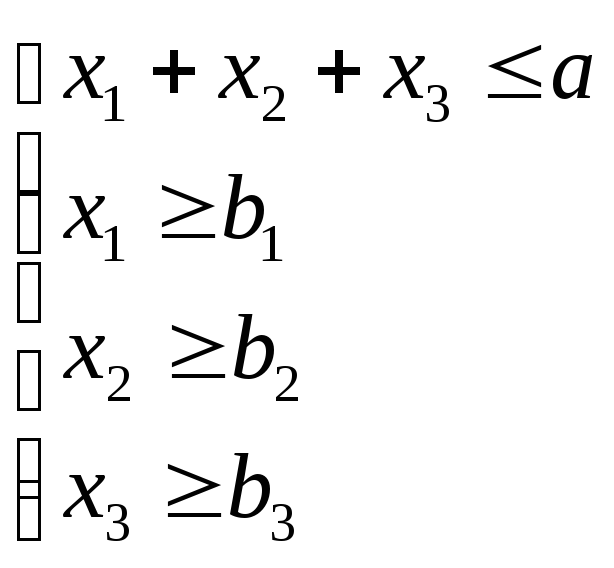
1. Дослідити систему лінійних нерівностей на сумісність.

а) за крітерієм Александрова,

б) за крітерієм Чернікова.

2. Розв’язати систему нерівностей

а) зведенням до системи рівнянь з 7 невідомими,

б) методом послідовного зменшення кількості невідомих.

3. Знайти мінімальні грані многогранника розв’язків заданої системи лінійних нерівностей.

4. Сформулювати стандартну та канонічну задачі для данної системи обмежень та цільової функції f.

5. Розв’язати симплекс - методом канонічну задачу, тобто знайти max (min) функції f на М.

Таблиця параметрів.

Варіант	A	b1	b2	b3	C1	C2	C3	f
1.	9	1	3	-1	-1	2	-3	min
2.	10	2	-2	3	2	-3	-1	max
3.	11	3	2	-2	-2	1	-5	min
4.	13	-1	2	4	-4	2	-5	max
5.	12	3	-1	2	1	-2	-3	max
6.	15	-1	3	1	4	-5	-6	min
7.	14	2	2	-1	2	-5	-3	max
8.	13	-2	2	1	3	-3	-2	min
9.	12	-4	1	3	-2	-4	1	max
10.	11	2	-1	5	3	-6	-2	min

Зразки розв’язання задач контрольної роботи №5

І. Знайти область розв’язків системи лінійних нерівностей.

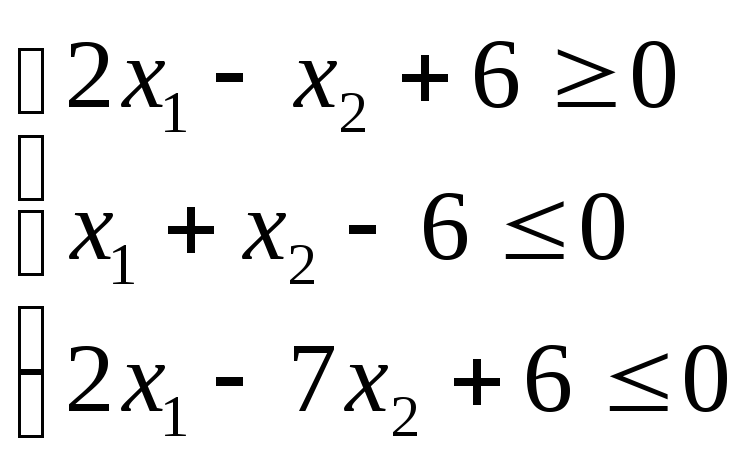
Розв’язання. Запишемо дану систему так:

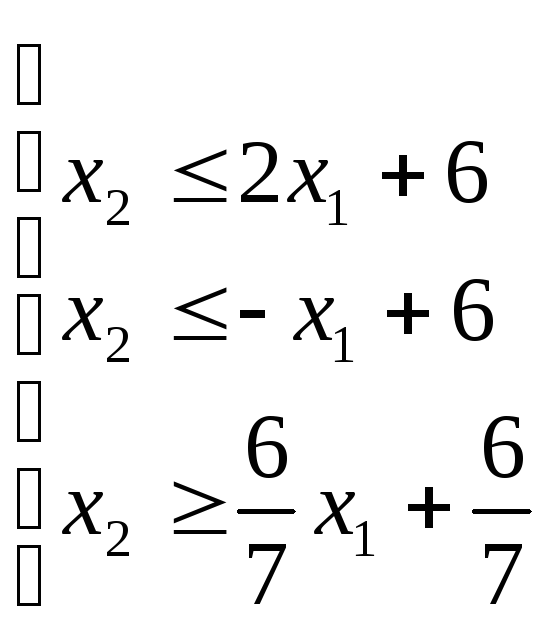
Перша нерівність цієї системи визначає півплощину, розміщену нижче від прямої ; друга нерівність визначає півплощину, розміщену нижче від прямої; третя – півплошину, розміщену вище від прямої;

На малюнку напрям стрілок показує ту півплощину, яка визначаєтся відповідною нерівністю. Областю розв’язків данної системи нерівностей є трикутник АВС. Визначемо координати його вершин. Для цього знаходимо розв’язки таких систем рівнянь:

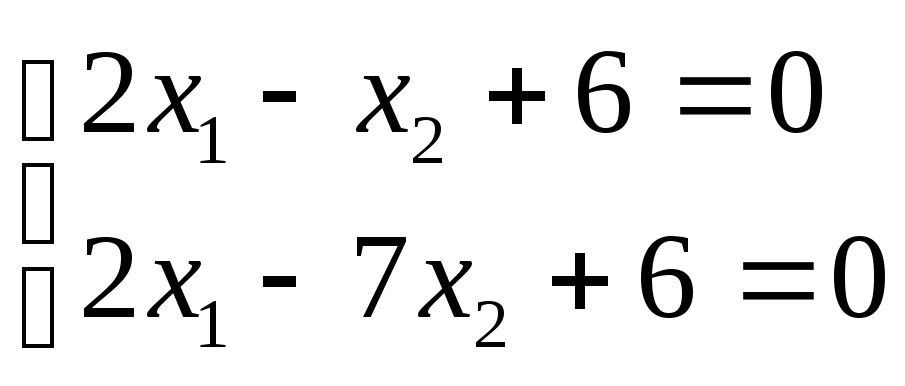
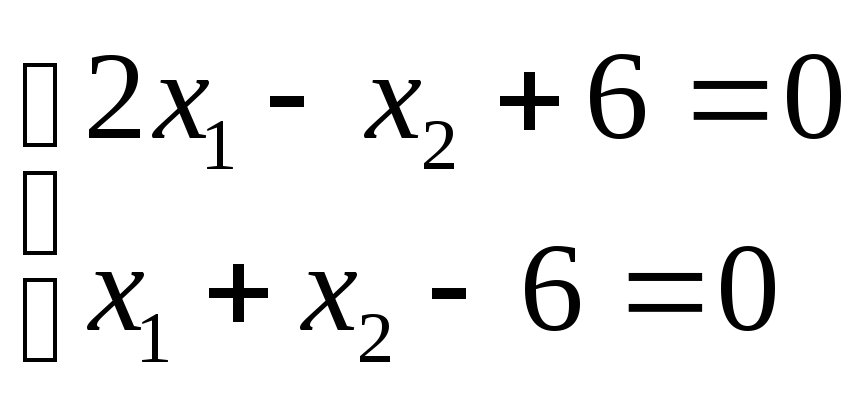
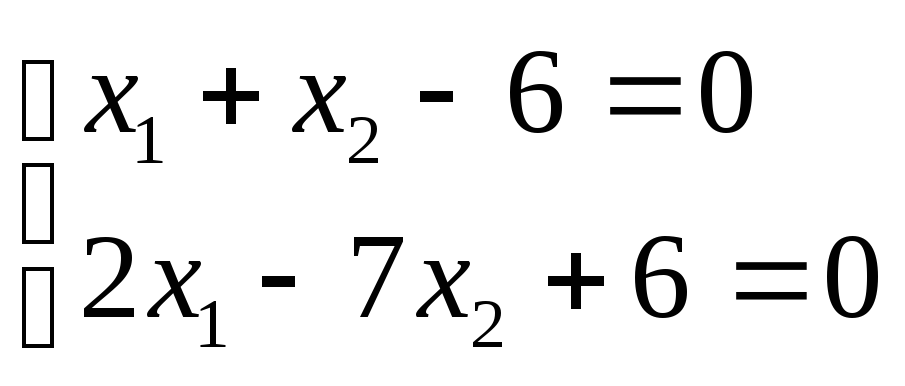
Розв‘язавши їх, маємо:

А(-3,0); В(0,6); С(4,2);

ІІ. Дана система лінійних нерівностей

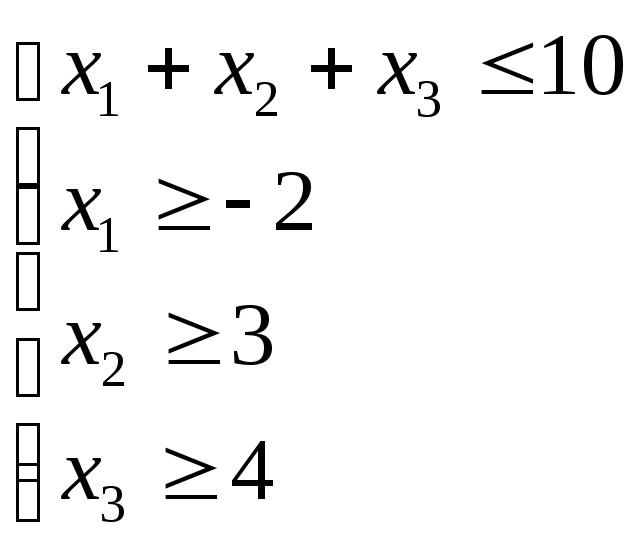
і функция .

1.Дослідити систему лінійних нерівностей на сумісність

а)критерієм Александрова

б)критерієм Чернікова

2.Розв’язати систему нерівностей

а)зведенням до системи рівнянь з 7 навідомими, ,;

б)методом послідовного зменшення кількості невідомих

3.Знайти мінімальні грані многогранника розв’язків.

4.Побудувати многогранники М і М⁺(додатніх розв’язків систем)

5.Сформулювати загальну стандартну та канонічну задачі для заданої системи обмежень та цільвої функції f

6.Розв’язати симплекс-методом канонічну задачу.

Розв’язання

1.

а)запишемо систему нерівностей у вигляді

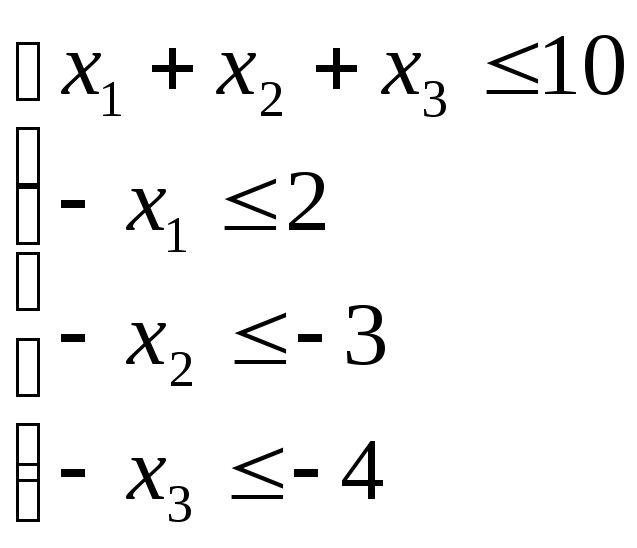
За критерієм Александрова система лінійних нерівностей несумісна тоді і тільки тоді, коли система лінійних рівнянь

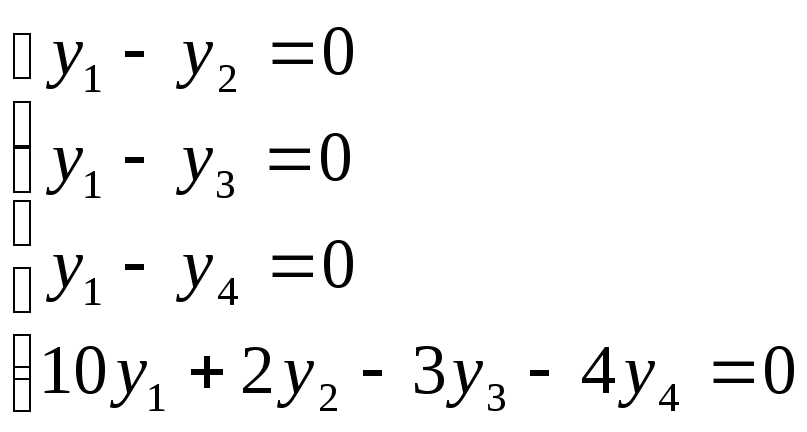
має невід’ємні розв’язки.

Розв’яжемо одержану систему лінійних рівнянь.

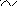
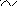
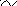
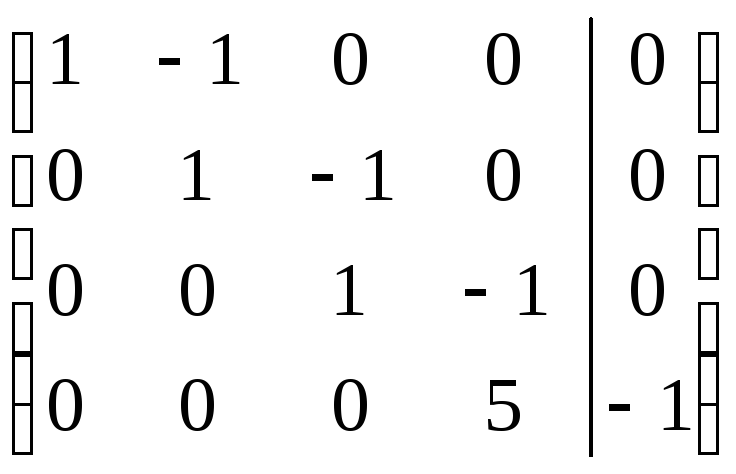
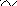
отже система лінійних рівнянь сумісна і має єдиний розв’язок.

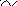
Розв’язком цієї системи є вектор , тобто розв’язок від’ємний, і тому система лінійних нерівностей сумісна.

б)дослідемо систему лінійних нерівностей на сумісність за крітерієм Чернікова.

Обчислюємо ранг матриці системи лінійних нерівностей:

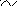
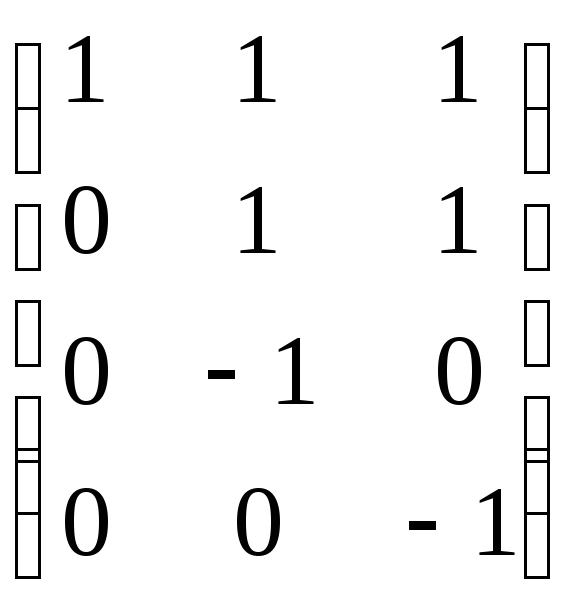
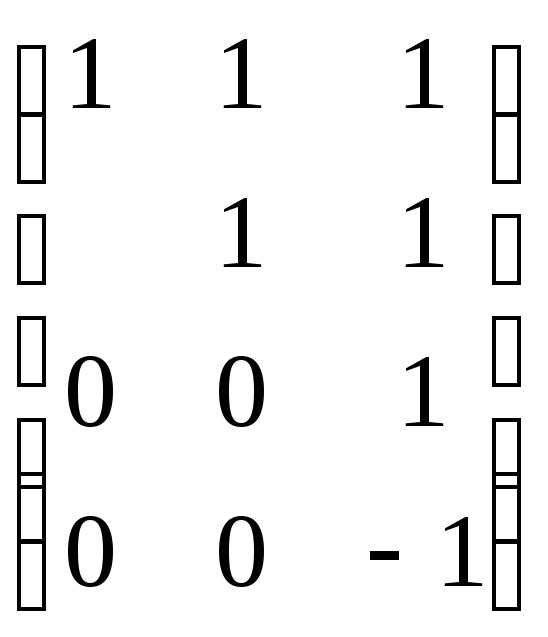
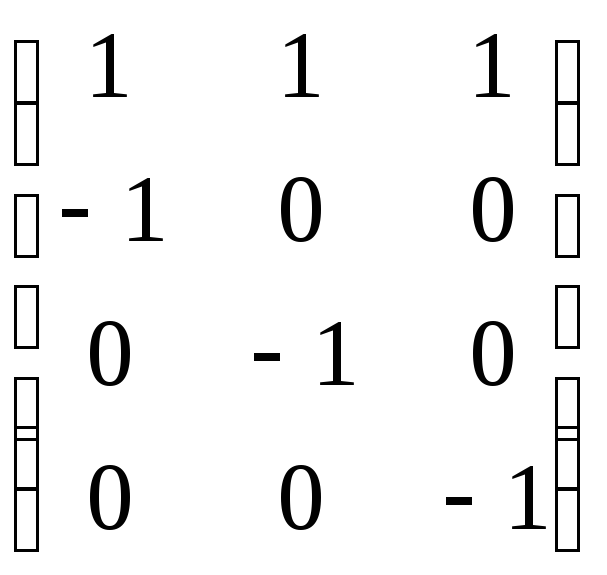r=3

Знаходимо відмінні від нуля мінори третього порядку:

;;

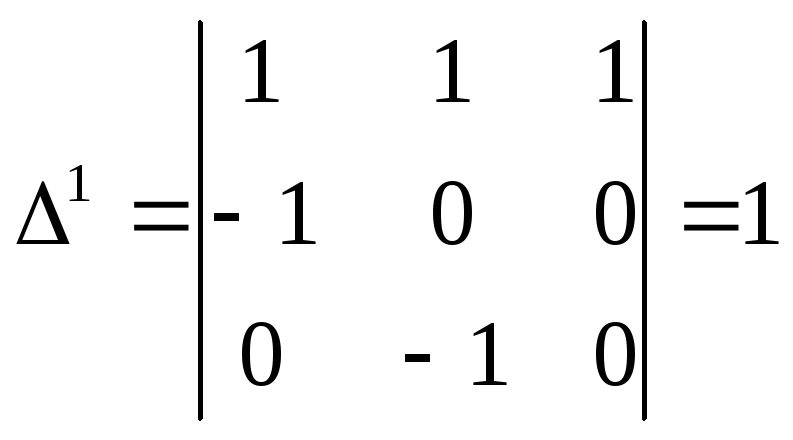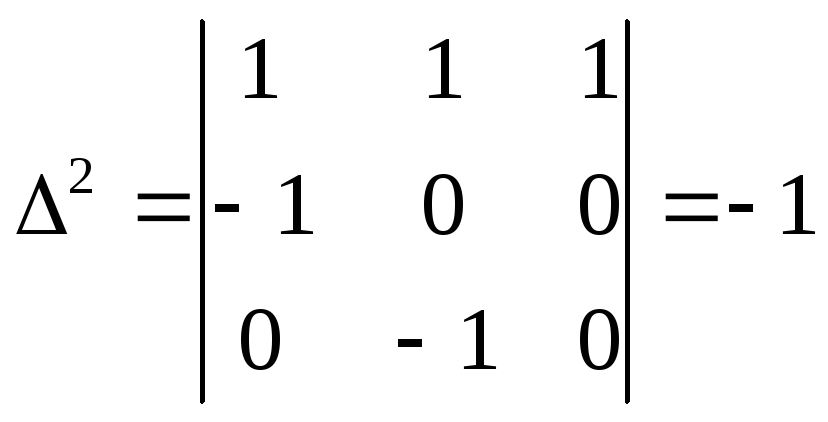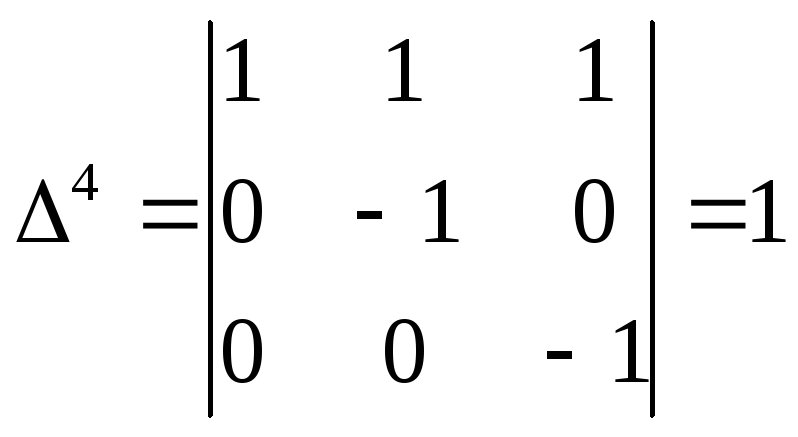
Супроводжуючі мінори:

оскількианалогічно

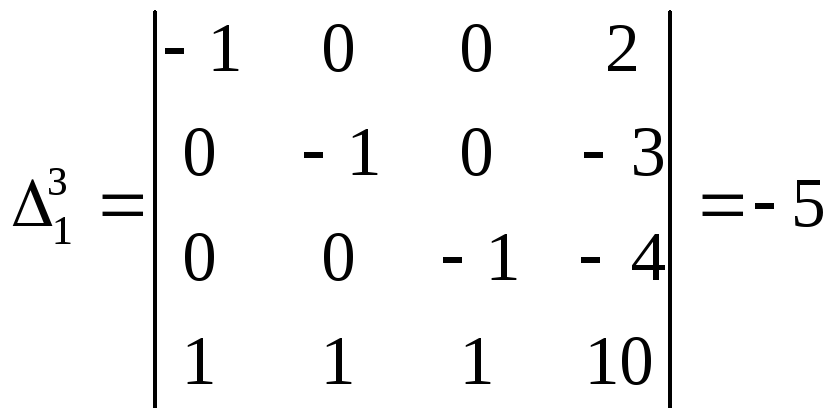
Відношення

Отже, за крітерієм Чернікова система лінійних нерівностей сумісна.

2. а)системі лінійних нерівностей поставимо у відповідність систему лінійних рівнянь:

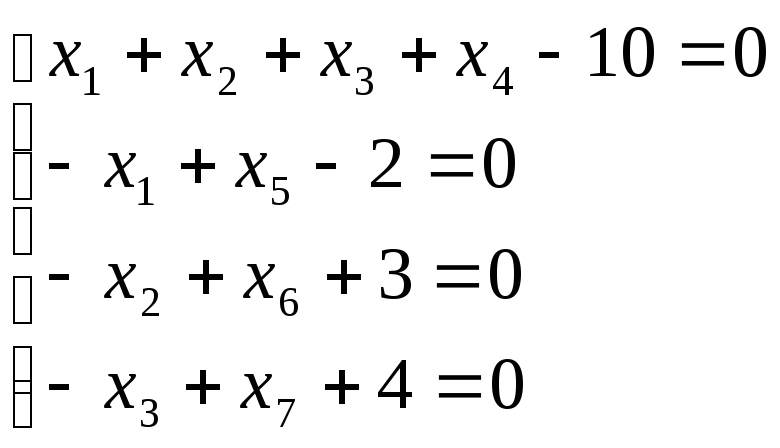
Розв’яжемо одержану систему лінійних рівнянь. Загальний розв’язок шукаємо у вигляді , де- частинний розв’язок,- загальний розв’язок відповідної однорідної системи лінійних рівнянь.

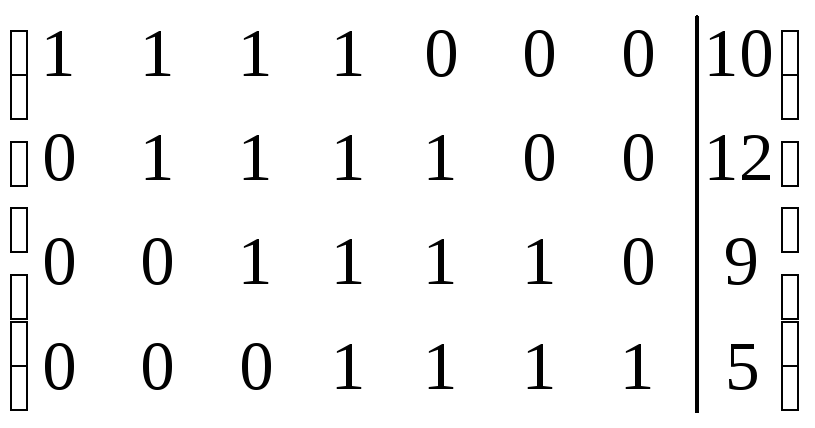
Система лінійних рівнянь сумісна і має безліч розв’язків (r<n).

Розв‘язуємо систему

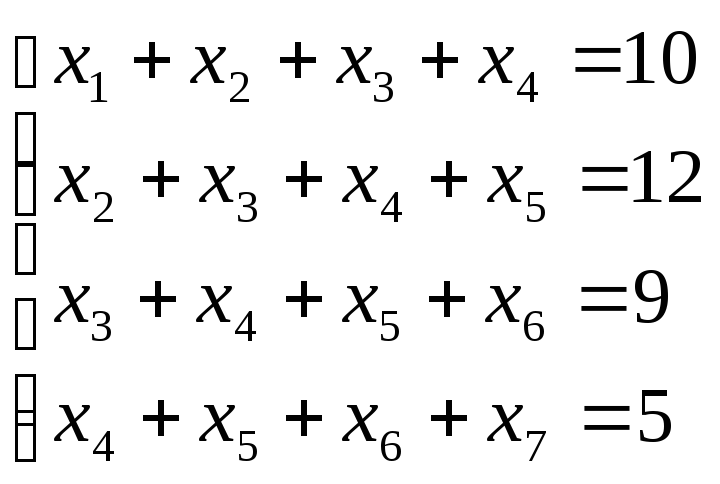
Знаходимо частинний розв’язок . Нехай– вільні невідомі. Надамонульових значень, тобто

Тоді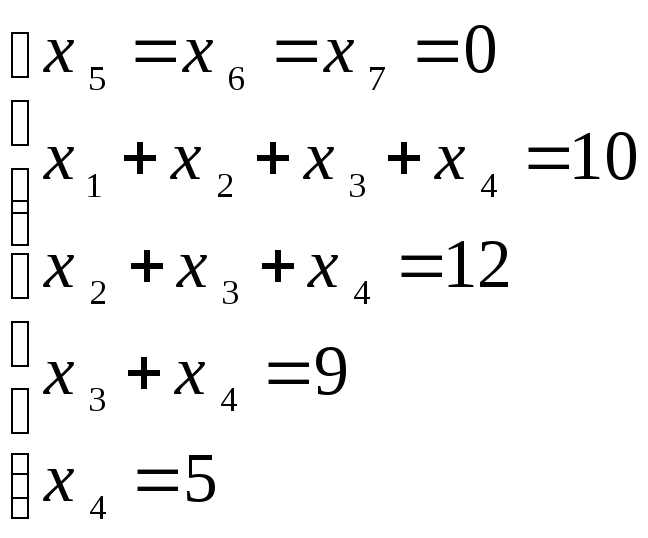

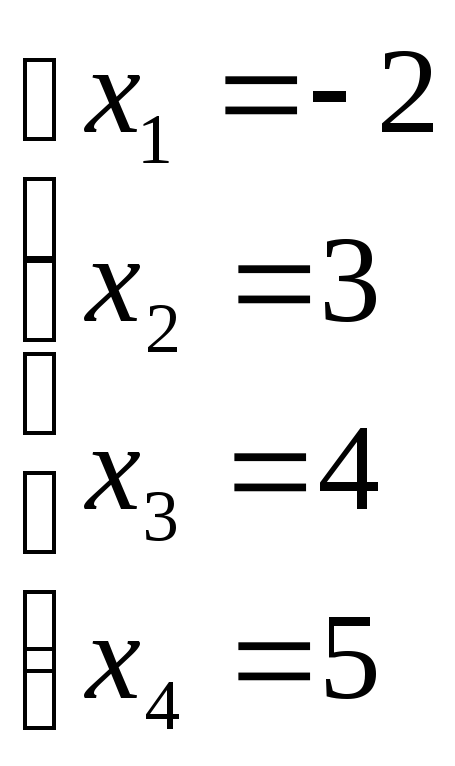
Отже, .

Відповідна однорідна система лінійних рівнянь має вид:

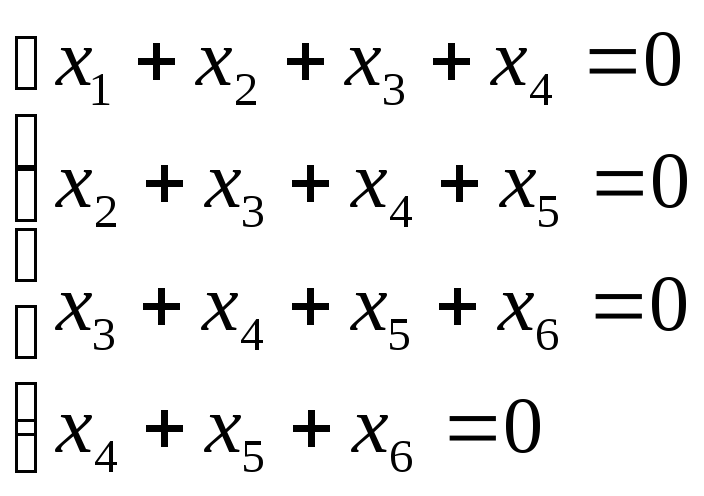
Фундаментальна система розв’язків цієї системи складаєтся з трьох векторів. У просторі R₃обираємо базис з векторів

і вільним невідомим послідовно надаємо значень ціого базису.

Нехай

тоді

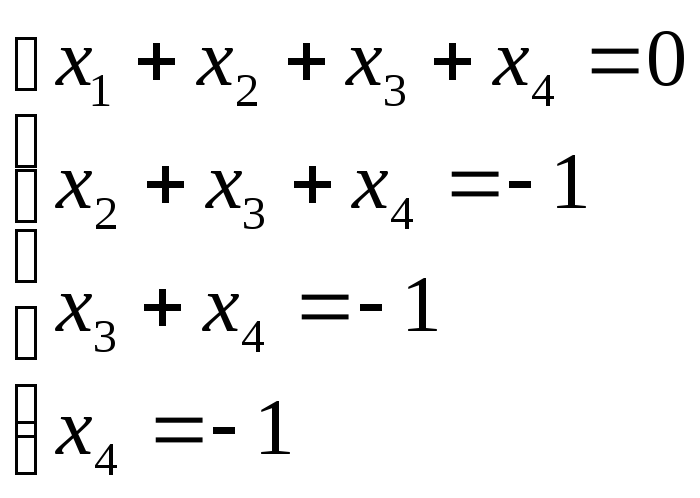
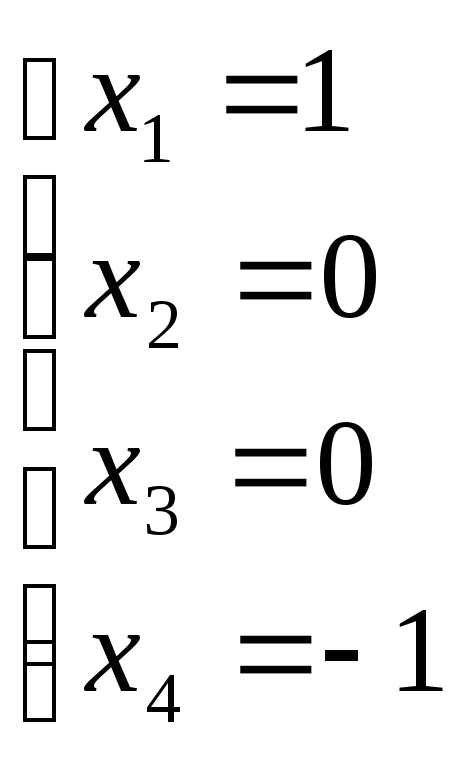
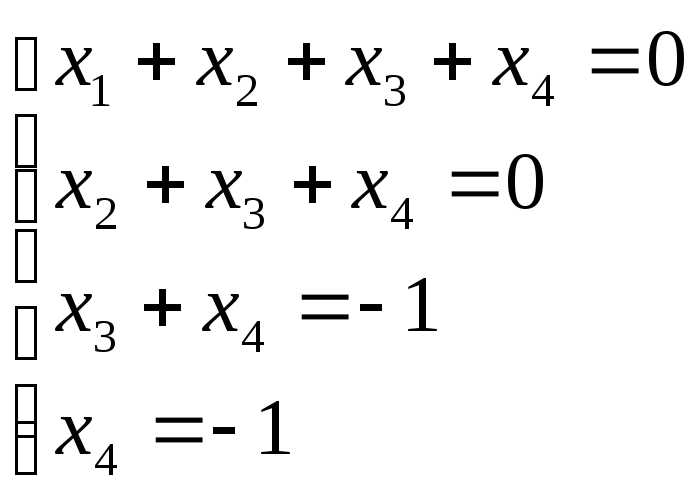
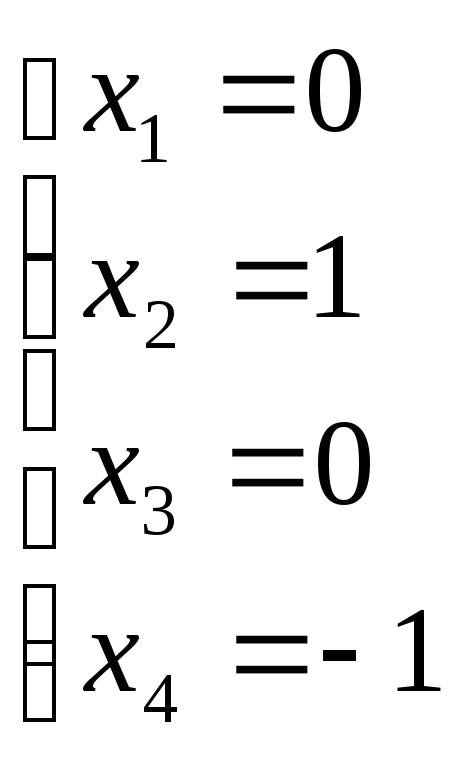
отже

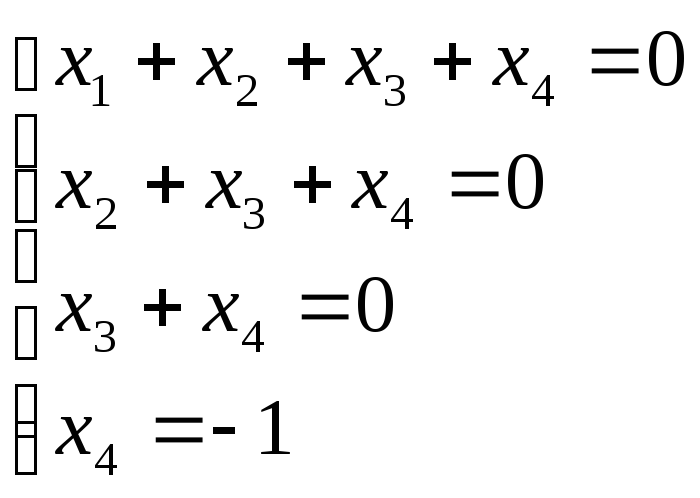
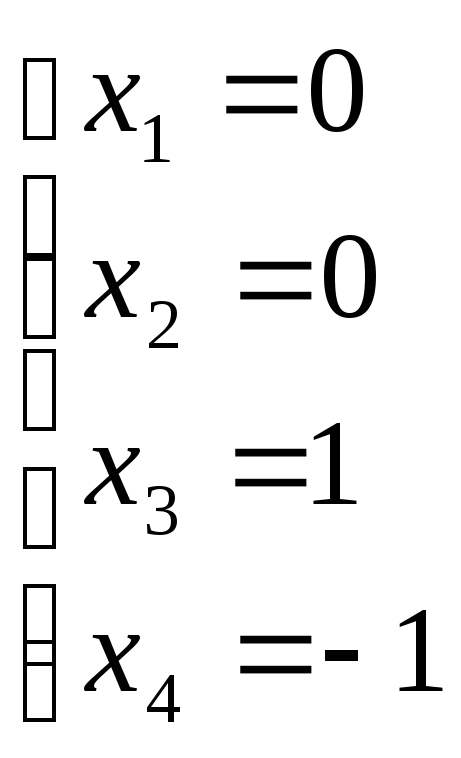Нехай тоді

тоді

Загальний розвя’зок однорідної системи рівнянь є лінійна комбінація векторів фундаментальної системи розв’язків, тобто

=

Загальний розв’язок системи неоднорідних рівнянь:

Отже, розв’язком системи лінійних нерівностей є вектор

причому

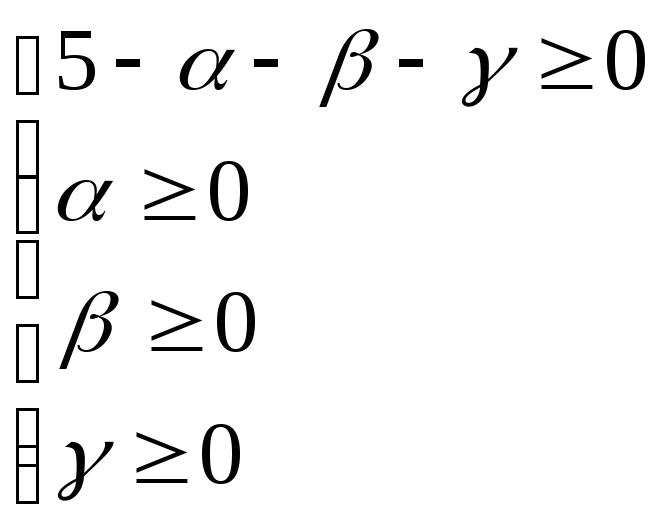оскільки

б) Розв’яжемо системи лінійних нерівностей методом послідовного зменшення кількості невідомих.

Запишемо систему у вигляді

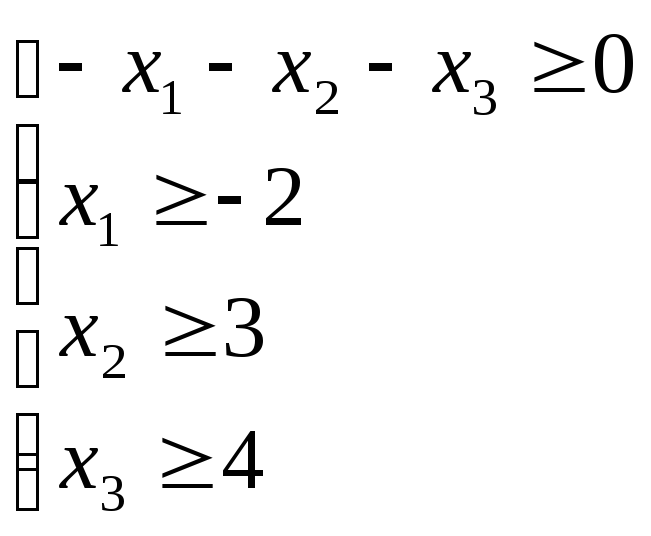
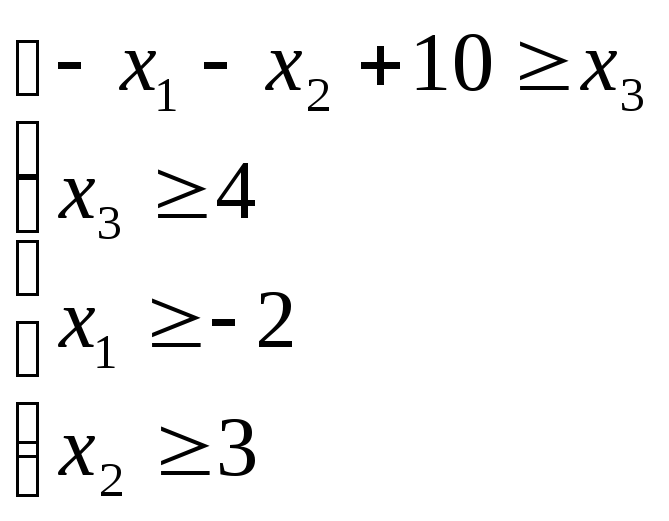
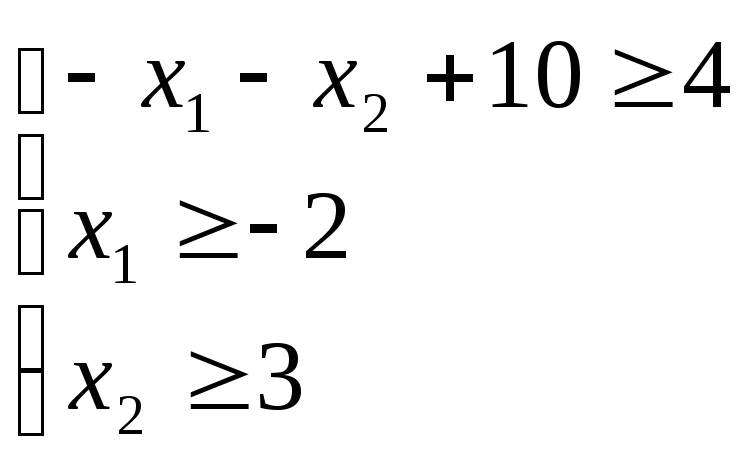
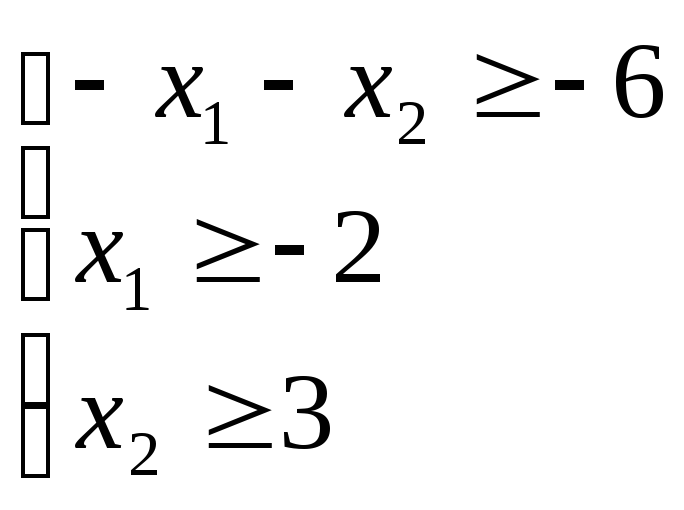
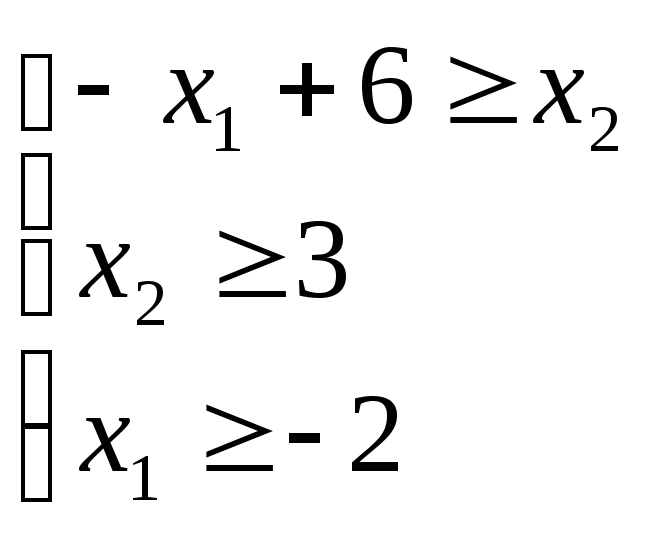
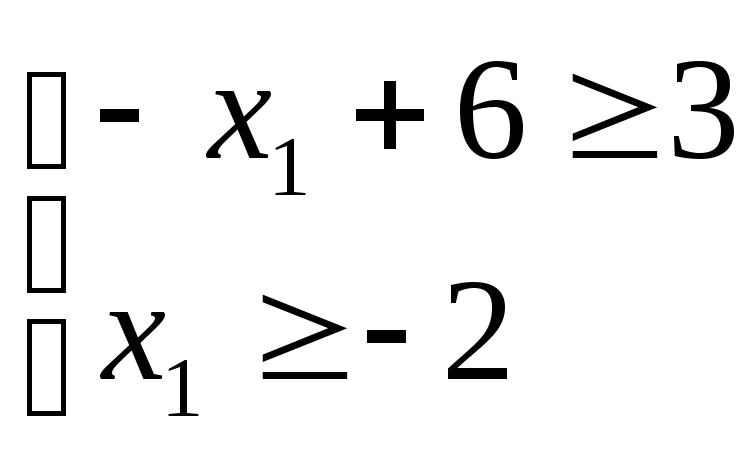
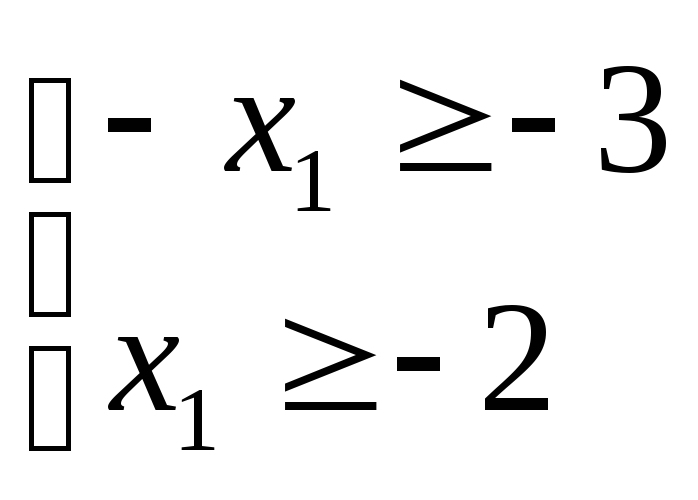
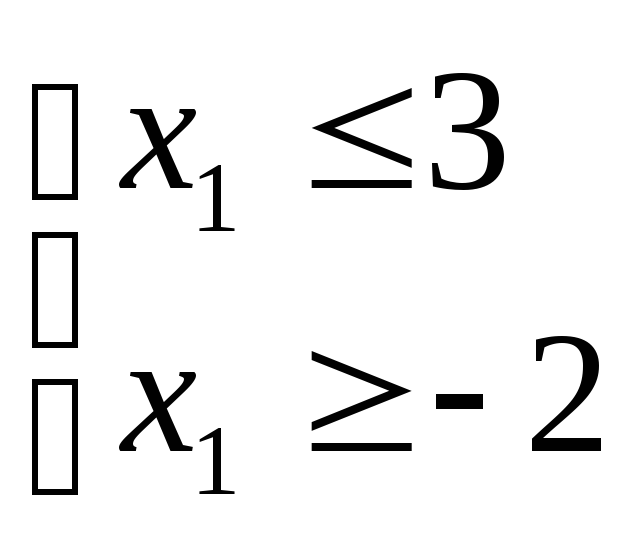
Нехай тоді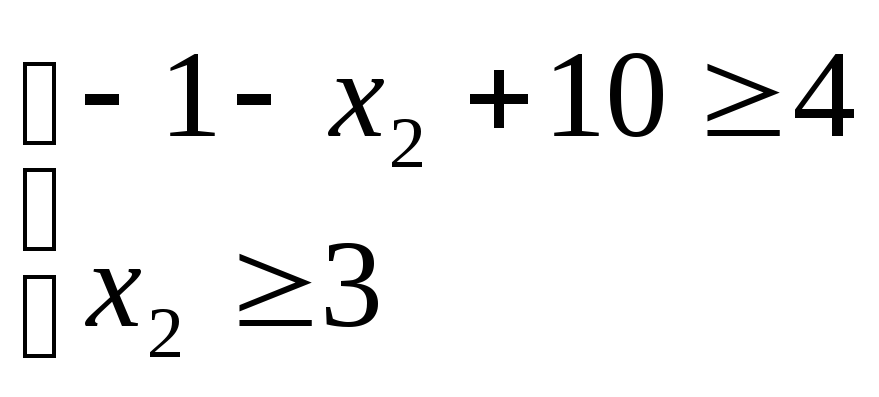

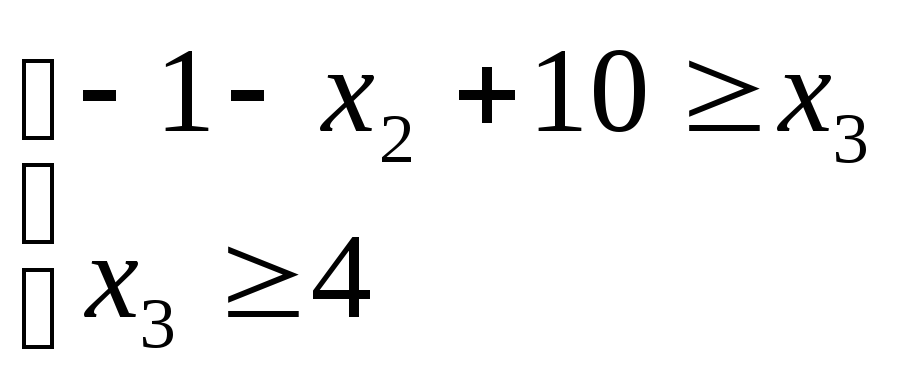
Нехай тодіотже

Звідси випливає, що вектор (1;4;4,5) є одним з розіязків системи лінійних нерівностей.

З загального розв’язку системи лінійних нерівностей можна одержати розв’язок (1;4;4,5) якщо

3.Знайдемо лінійні грані многогранника розв’язків системи лінійних нерівностей.

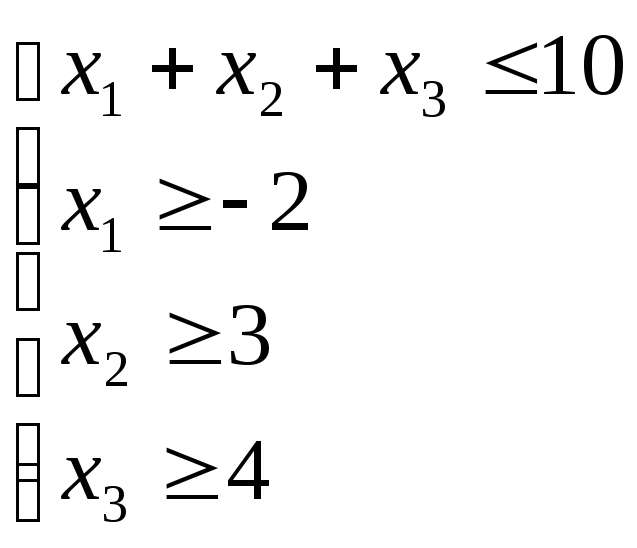
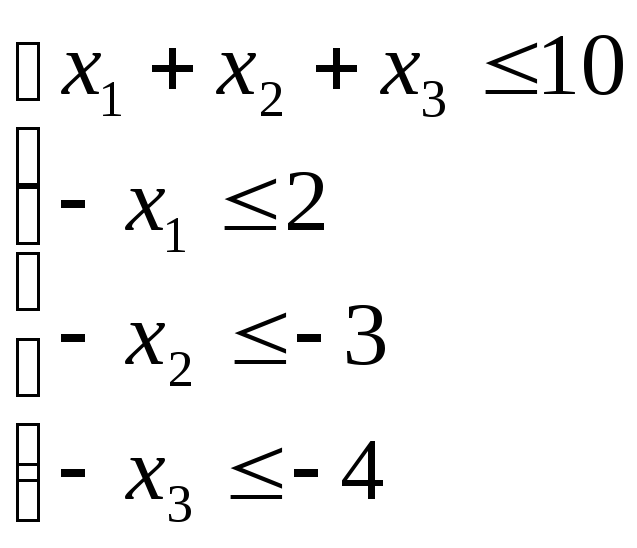
Обчислюємо ранг системи нерівностей

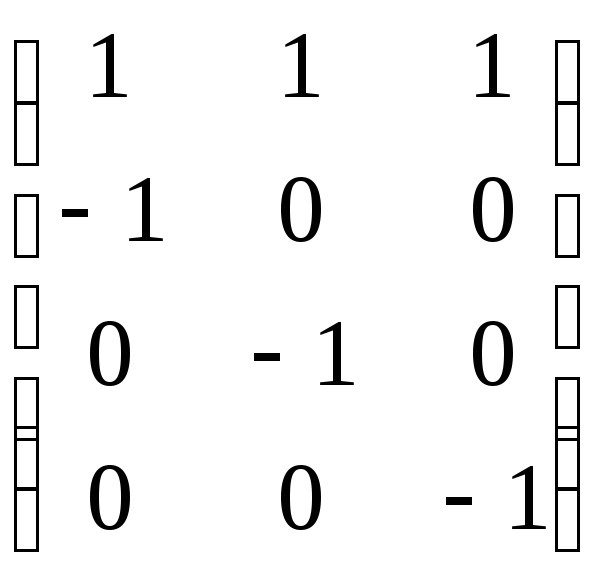
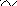
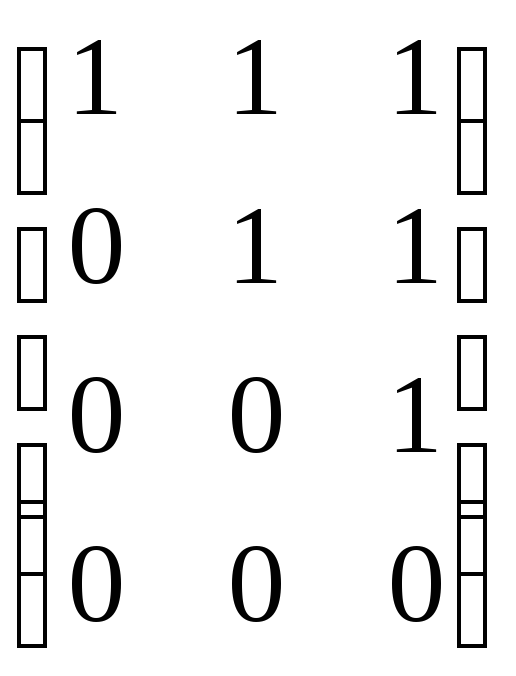
Виписуємо з даної системи рангу 3 усі лінійно незалежні підсистеми лінійних нерівностей та замінюємо їх системами рівнянь, що одержуются в результаті заміни в системах нерівностей знаку нерівності на знак рівності.

Одержуємо

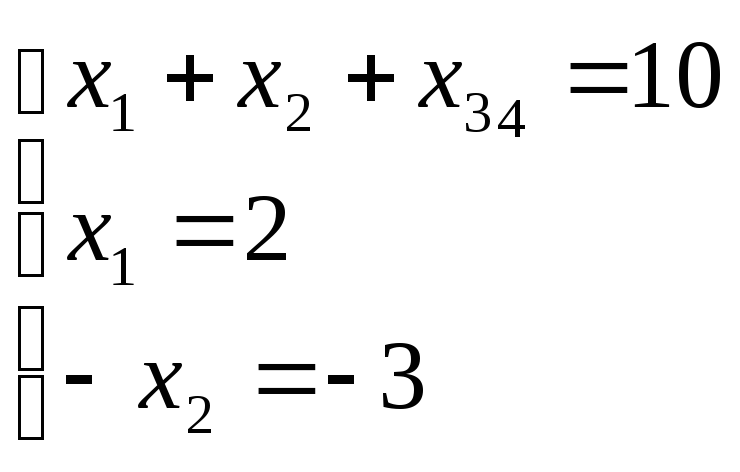
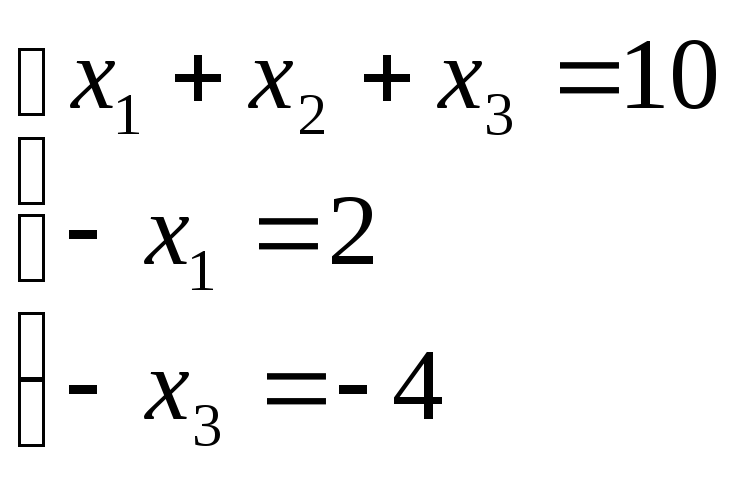
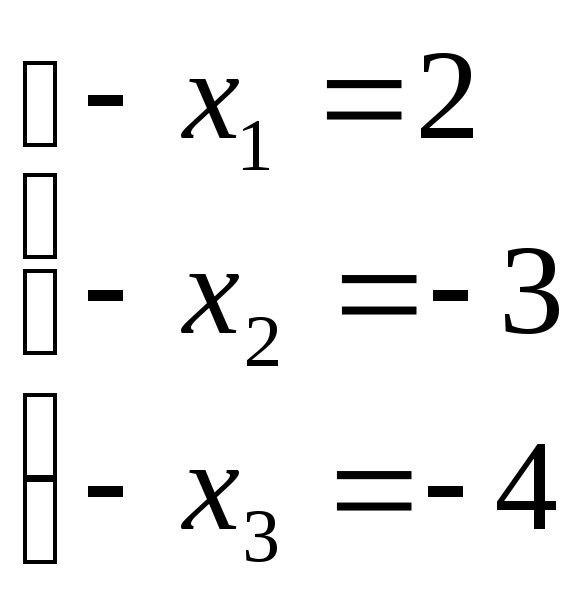
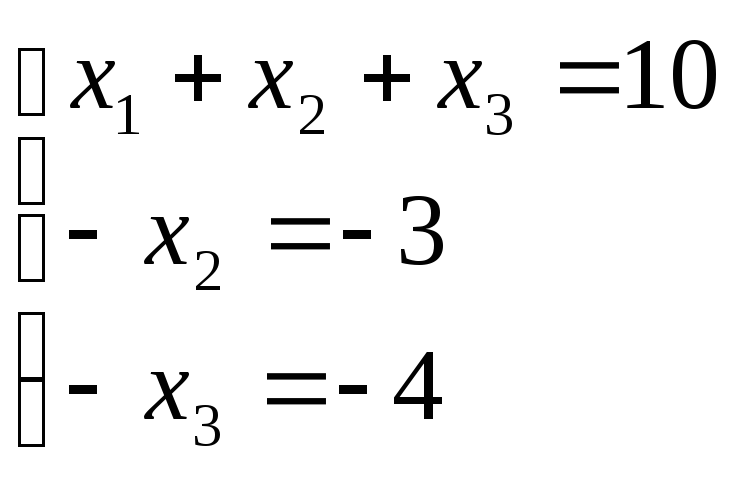
Оскільки ранг кожної з систем дорівнює кількості невідомих, то вони всі мають по єдиному розвязку.

Розв’яжемо ці системи. Одержуємо

(-2,8,4); (-2,3,4); (3,3,4) – розв’язки відповідних систем рангуr= 3.

Ці розв’язки задовольняють і системі лінійних нерівностей рангу r=3=n, тому є вершинами многогранника, тобто мінімальними гранями многогранника розв’язків.

4.Сформулюємо стандартну та канонічну задачі для данної системи обмежень та цільової функції f.

Стандартна задача:

Знайти maxфункціїf=3x₁-4x₂-2x₃на множині невід’ємних розвязків системи нерівностей

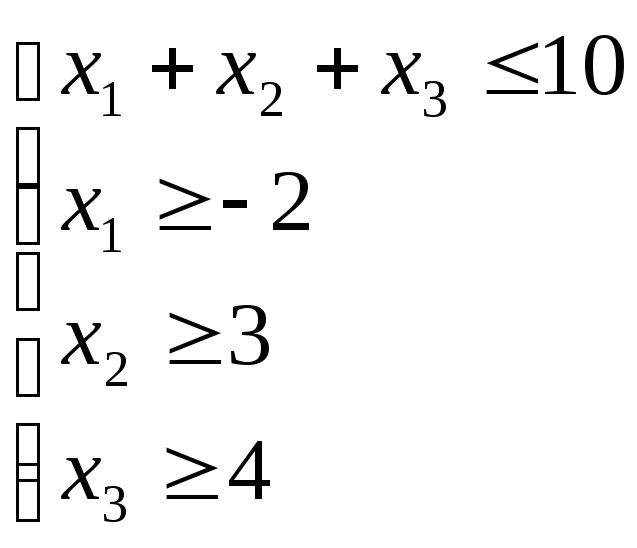або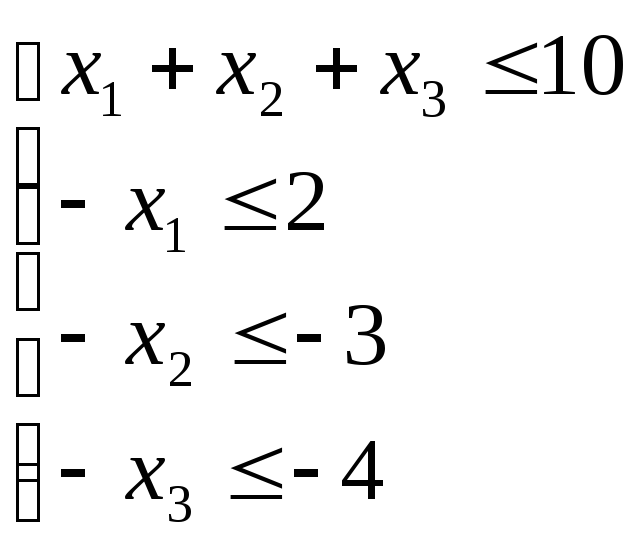

Канонічна задача:

Знайти maxфункціїf=3x₁-4x₂-2x₃на множині невід’ємних розв’язків системи рівнянь

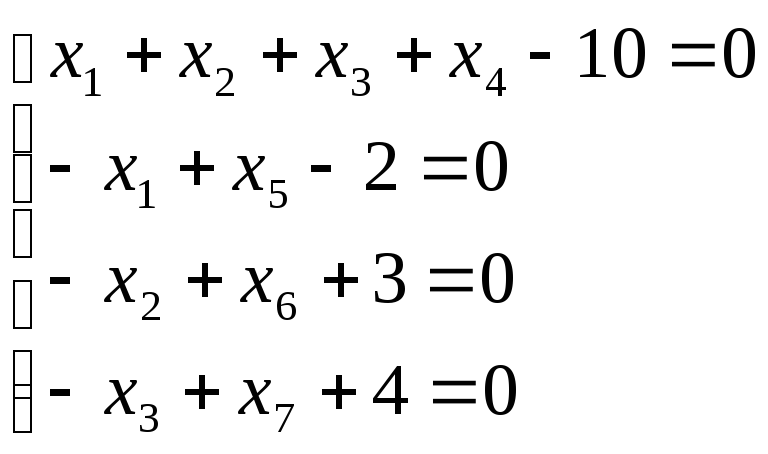
5.Розв’яжемо симплекс-методом канонічну задачу.

Знаходимо будь-який базисний невід’ємний розв’язок системи лінійних рівнянь.

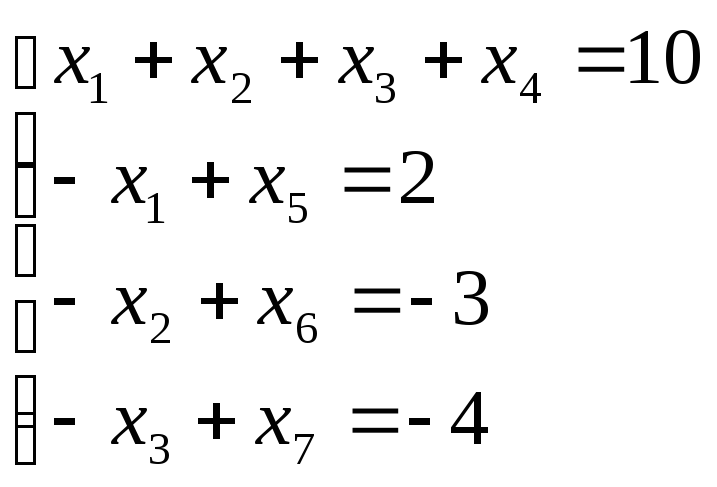
Ранг цієї системи r=4, отже,

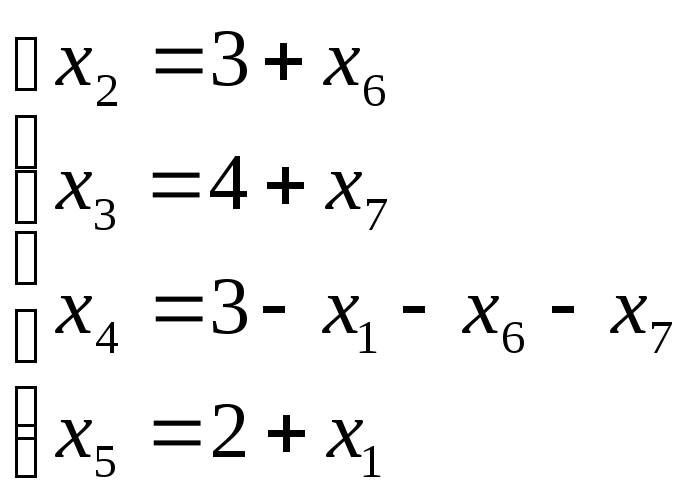
Оскільки ранг системи дорівнює 4, то за вільні невідомі можна обрати x₁, x₆, x₇,за основні базисні невідомі -x₂, x₃, x₄, x₅.

Нехай x₁ =x₆ =x₇ = 0, тодіx₂=3;x₃=4;x₄=3;x₅=2 - невід’ємний розв’язок системи лінійних рівнянь. Виражаємо цільову функціюfчерез вільні невідоміx₁, x₆, x₇, одержуємо

Отже , і система лінійних рівнянь – обмежень рівносильна системі обмежень функції, виражаємо через вільні невідомі:

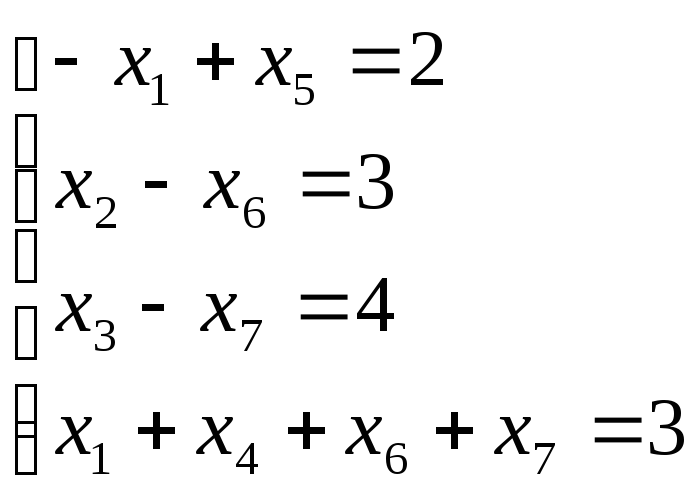
Складаємо симплекс – таблицю 1.

Базисні невідомі	X1	X2	X3	X4	X5	X6	X7	Вільні члени
	0	1	0	0	0	-1	0	3
	0	0	1	0	0	0	-1	4
	1	0	0	1	0	1	1	3
	-1	0	0	0	1	0	0	2
	-3	0	0	0	0	4	2	-20

Оптимального розв’язку немає; в рядкуfє від’ємний коефіцієнт. Переходимо до таблиці 2.

Базисні невідомі	X1	X2	X3	X4	X5	X6	X7	Вільні члени
X2	0	1	0	0	0	-1	0	3
X3	0	0	1	0	0	0	-1	4
X1	1	0	0	1	0	1	1	3
X5	0	0	0	1	1	1	1	5
f	0	0	0	3	0	7	5	-11

Оскільки в рядку f таблиці 2 всі коефіцієнти додатні, то оптимальний розв’язок канонічної задачі одержано:

max f = -11при додатньому розв’язку (3,3,4,0,5,0,0) системи.

Отже, отриманий розв’язок стандартної задачі єmax f = -11 при значеннях невідомих системи обмежень (3,3,4).